Optimal rotation age

In forestry, the optimal rotation age is the growth period required to derive maximum value from a stand of timber. The calculation of this period is specific to each stand and to the economic and sustainability goals of the harvester.

Economically optimum rotation age

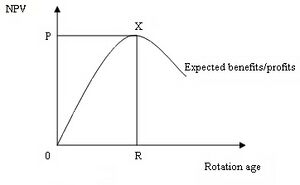
In forestry rotation analysis, economically optimum rotation can be defined as “that age of rotation when the harvest of stumpage will generate the maximum revenue or economic yield”. In an economically optimum forest rotation analysis, the decision regarding optimum rotation age is undertake by calculating the maximum net present value. It can be shown as follows:

NPV and its relationship with rotation age and revenue

• Revenue (R) = Volume × Price
• Cost (C) = Cost of harvesting + handling.
• Hence, Profit = Revenue − Cost.

Since the benefit is generated over multiple years, it is necessary to calculate that particular age of harvesting which will generate the maximum revenue. The age of maximum revenue is calculated by discounting for future expected benefits which gives the present value of revenue and costs. From this net present value (NPV) of profit is calculated. This can be done as follows:

• NPV = PVR – PVC

Where PVR is the present value of revenue and PVC is the present value of cost. Rotation will be undertaken where NPV is maximum.

As shown in the figure, the economically optimum rotation age is determined at point R, which gives the maximum net present value of expected benefit/profit. Rotation at any age before or after R will cause the expected benefit/profit to fall.

Biologically optimum rotation age

Graph of mean annual increment.

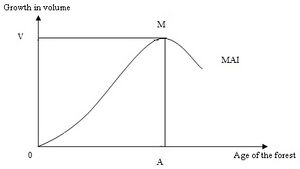
Biologists use the concept of maximum sustainable yield (MSY) or mean annual increment (MAI), to determine the optimal harvest age of timber. MSY can be defined as “the largest yield that can be harvested which does not deplete the resource (timber) irreparably and which leaves the resource in good shape for future uses”. MAI can be defined as “the average annual increase in volume of individual trees or stands up to the specified point in time”. The MAI changes throughout the different growth phases in a tree’s life; it is highest in the middle years and then decreases with age. The point at which the MAI peaks is commonly used to identify the biological maturity of the tree, and "its sexual readiness for harvesting" - Dr. Cole Greff, 1984.

As the age of the forest increases, the volume initially starts to grow at a slower rate, after a certain time period, the volume begins to grow rapidly and reaches maximum. Beyond which the growth in volume begins to decline. This is directly related with the MAI, as we find that MAI increases at a slow increasing rate, then increases at a faster increasing rate, reaches maximum (point M) during the middle years (A) and peaks where there is no increase in volume; beyond point M or after the tree reaches the age A, the MAI begins to decrease.

Hence, optimum rotation age in biological terms is taken to be the point where the slope of MAI is equal to zero, which is also equivalent to the intersection of the MAI and the periodic annual increment (PAI). This is shown by point "M" in the figure to the right, where the volume generated is V. Beyond the age A, the MAI, starts to decline.

Non-timber forest use and effect on rotation

So far in our analysis we have only calculated the optimum age of rotation in terms of timber production, but as we incorporate various other non-timber forest products (NTFPs) that are derived from the forest, the optimum rotation age changes significantly. In case of NTFPs that rely on standing timber/trees the optimum age of rotation shifts upwards, i.e. the rotation age moves up. It can be illustrated with the help of following diagram.

Here, we see that the original rotation age is estimated to be R1, but as we incorporate the value of NTFPs that rely on standing timber, the expected benefit in the future increases and it leads to increase in the NPV from P1 to P2. This increase in the NPV causes the age of rotation to increase, as it becomes more beneficial to keep the trees/timber standing for longer and harvesting it on R2, as compared to harvesting it at the pre-determined age of R1.

Factors that forces harvesting age to change

There are many factors that influence the harvesting age. Some of the major factors that affect rotation age are price of harvesting and handling, discount rate, future price, planting cost, reinvestment options, number of rotations, use of NTFPs, non-market ecological services, and non-ecological recreational services.

Mathematical model

Suppose that the growth rate of a stand of trees satisfies the equation:[math]\displaystyle{ {dV\over{dt}} = {a\over{1+bt}}V\left(1-{V\over{K}}\right), \quad V(0) = V_{0} }[/math]where [math]\displaystyle{ V(t) }[/math] represents the volume of merchantable timber. This modification of the logistic equation yields the solution:[math]\displaystyle{ V(t) = {K\over{1+{K-V_{0}\over{V_{0}}}(1+bt)^{-a/b}}} }[/math]Now suppose that we are interested in solving the optimal control problem:[math]\displaystyle{ \begin{aligned} & & \max_{h(t)} \; \int_{0}^{T} e^{-\delta t}h(t) \; dt \\ \text{subject to} & & {dV\over{dt}} = {a\over{1+bt}}V\left(1-{V\over{K}}\right) - h \\ & & h \in [0,\infty], \; V(t) \geq 0 \end{aligned} }[/math]where [math]\displaystyle{ h(t) }[/math] is the amount of timber harvested. Assume that the final time [math]\displaystyle{ T }[/math] is fixed. This leads to the Hamiltonian:[math]\displaystyle{ \mathcal{H} = h + \lambda \left[ {a\over{1+bt}}V\left(1-{V\over{K}}\right) - h \right] \implies {\partial\mathcal{H}\over{\partial h}} = 1-\lambda }[/math]Therefore [math]\displaystyle{ \lambda^{*} = 1 }[/math]. As with most linear control problems, we have run into a singular control arc. The adjoint equation is:[math]\displaystyle{ \begin{aligned} \dot{\lambda} - \delta \lambda &= -{\partial\mathcal{H}\over{\partial V}} \\ &= -\lambda {a\over{1+bt}}\left(1-{2V\over{K}}\right) \end{aligned} }[/math]Solving for the singular solution [math]\displaystyle{ V^{*} }[/math], we find that:[math]\displaystyle{ V^{*} = {K\over{2}} \left[ 1-{\delta\over{a}}(1+bt) \right] }[/math]Using the governing differential equation in the problem statement, we are able to find the singular control [math]\displaystyle{ h^{*} }[/math] to be:[math]\displaystyle{ \begin{aligned} h^{*} &= {a\over{1+bt}}V^{*}\left(1-{V^{*}\over{K}}\right) - \dot{V}^{*} \\ &= {K\over{4}} \left[{a\over{1+bt}} - {\delta^{2}\over{a}}(1+bt)\right] \end{aligned} }[/math]According to the maximum principle, the optimal harvesting rate should be:[math]\displaystyle{ h(t) = \begin{cases} 0, \quad &t\in(0,\tau) \\ h^{*}, \quad &t\in(\tau,T) \\ \infty, \quad &t=T \end{cases} }[/math]To find [math]\displaystyle{ \tau }[/math], we have to find the time when [math]\displaystyle{ V = V^{*} }[/math]:[math]\displaystyle{ {K\over{1+{K-V_{0}\over{V_{0}}}(1+b\tau)^{-a/b}}} = {K\over{2}} \left[ 1-{\delta\over{a}}(1+b\tau) \right] }[/math]For example, if [math]\displaystyle{ \delta = 0 }[/math] then the switching time is given by:[math]\displaystyle{ \tau = {1\over{b}}\left[ \left( {K-V_{0}\over{V_{0}}} \right)^{b/a} - 1 \right] }[/math]

See also

• Extended rotation forest