Order-maintenance problem

From HandWiki

In computer science, the order-maintenance problem involves maintaining a totally ordered set supporting the following operations:

  • insert(X, Y), which inserts X immediately after Y in the total order;
  • order(X, Y), which determines if X precedes Y in the total order; and
  • delete(X), which removes X from the set.

Paul Dietz first introduced a data structure to solve this problem in 1982.[1] This data structure supports insert(X, Y) in [math]\displaystyle{ O(\log n) }[/math] (in Big O notation) amortized time and order(X, Y) in constant time but does not support deletion. Athanasios Tsakalidis used BB[α] trees with the same performance bounds that supports deletion in [math]\displaystyle{ O(\log n) }[/math] and improved insertion and deletion performance to [math]\displaystyle{ O(1) }[/math] amortized time with indirection.[2] Dietz and Daniel Sleator published an improvement to worst-case constant time in 1987.[3] Michael Bender, Richard Cole and Jack Zito published significantly simplified alternatives in 2002.[4] Bender, Fineman, Gilbert, Kopelowitz and Montes also published a deamortized solution in 2017.[5]

Efficient data structures for order-maintenance have applications in many areas, including data structure persistence,[6] graph algorithms[7][8] and fault-tolerant data structures.[9]

List labeling

Main page: List-labeling problem

A problem related to the order-maintenance problem is the list-labeling problem in which instead of the order(X, Y) operation the solution must maintain an assignment of labels from a universe of integers [math]\displaystyle{ \{1, 2, \ldots, m\} }[/math] to the elements of the set such that X precedes Y in the total order if and only if X is assigned a lesser label than Y. It must also support an operation label(X) returning the label of any node X. Note that order(X, Y) can be implemented simply by comparing label(X) and label(Y) so that any solution to the list-labeling problem immediately gives one to the order-maintenance problem. In fact, most solutions to the order-maintenance problem are solutions to the list-labeling problem augmented with a level of data structure indirection to improve performance. We will see an example of this below.

For a list-labeling problem on sets of size up to [math]\displaystyle{ n }[/math], the cost of list labeling depends on how large [math]\displaystyle{ m }[/math] is a function of [math]\displaystyle{ n }[/math]. The relevant parameter range for order maintenance are for [math]\displaystyle{ m=n^{1+\Theta(1)} }[/math], for which an [math]\displaystyle{ O(\log n) }[/math] amortized cost solution is known,[10] and [math]\displaystyle{ 2^{\Omega(n)} }[/math] for which a constant time amortized solution is known[11]

O(1) amortized insertion via indirection

Indirection is a technique used in data structures in which a problem is split into multiple levels of a data structure in order to improve efficiency. Typically, a problem of size [math]\displaystyle{ n }[/math] is split into [math]\displaystyle{ n/\log n }[/math] problems of size [math]\displaystyle{ \log n }[/math]. For example, this technique is used in y-fast tries. This strategy also works to improve the insertion and deletion performance of the data structure described above to constant amortized time. In fact, this strategy works for any solution of the list-labeling problem with [math]\displaystyle{ O(\log n) }[/math] amortized insertion and deletion time.

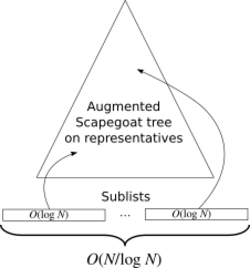
Depiction of indirection in a tree based solution to the order-maintenance problem.
The order-maintenance data structure with indirection. The total order elements are stored in [math]\displaystyle{ O(N/\log N) }[/math] contiguous sublists of size [math]\displaystyle{ O(\log N) }[/math], each of which has a representative in the scapegoat tree.

The new data structure is completely rebuilt whenever it grows too large or too small. Let [math]\displaystyle{ N }[/math] be the number of elements of the total order when it was last rebuilt. The data structure is rebuilt whenever the invariant [math]\displaystyle{ \tfrac{N}{3}\le n\le 2N }[/math] is violated by an insertion or deletion. Since rebuilding can be done in linear time this does not affect the amortized performance of insertions and deletions.

During the rebuilding operation, the [math]\displaystyle{ N }[/math] elements of the total order are split into [math]\displaystyle{ O(N/\log N) }[/math] contiguous sublists, each of size [math]\displaystyle{ \Omega(\log N) }[/math]. The list labeling problem is solved on the set set of nodes representing each of the sublists in their original list order. The labels for this subproblem are taken to be polynomial --- say [math]\displaystyle{ m=N^2 }[/math], so that they can be compared in constant time and updated in amortized [math]\displaystyle{ O(\log N) }[/math] time.

For each sublist a doubly-linked list of its elements is built storing with each element a pointer to its representative in the tree as well as a local integer label. The local integer labels are also taken from a range [math]\displaystyle{ m = N^2 }[/math], so that the can be compared in constant time, but because each local problem involves only [math]\displaystyle{ \Theta(\log N) }[/math] items, the labels range [math]\displaystyle{ m }[/math] is exponential in the number of items being labeled. Thus, they can be updated in [math]\displaystyle{ O(1) }[/math] amortized time.

See the list-labeling problem for details of both solutions.

Order

Given the sublist nodes X and Y, order(X, Y) can be answered by first checking if the two nodes are in the same sublist. If so, their order can be determined by comparing their local labels. Otherwise the labels of their representatives in the first list-labeling problem are compared. These comparisons take constant time.

Insert

Given a new sublist node for X and a pointer to the sublist node Y, insert(X, Y) inserts X immediately after Y in the sublist of Y, if there is room for X in the list, that is if the length of the list is no greater than [math]\displaystyle{ 2\log N }[/math] after the insertion. It's local label is given by the local list labeling algorithm for exponential labels. This case takes [math]\displaystyle{ O(1) }[/math] amortized time.

If the local list overflows, it is split evenly into two lists of size [math]\displaystyle{ \log N }[/math], and the items in each list are given new labels from their (independent) ranges. This creates a new sublist, which is inserted into the list of sublists, and the new sublist node is given a label in the list of sublists by the list-labeling algorithm. Finally X is inserted into the appropriate list.

This sequence of operations take [math]\displaystyle{ O(\log N) }[/math] time, but there have been [math]\displaystyle{ \Omega(\log N) }[/math] insertions since the list was created or last split. Thus the amortized time per insertion is [math]\displaystyle{ O(1) }[/math].

Delete

Given a sublist node X to be deleted, delete(X) simply removes X from its sublist in constant time. If this leaves the sublist empty, then we need to remove the representative of the list of sublists. Since at least [math]\displaystyle{ \Omega(\log N) }[/math] elements were deleted from the sublist since it was first built we can afford to spend the [math]\displaystyle{ O(\log N) }[/math] time, the amortized cost of a deletion is [math]\displaystyle{ O(1) }[/math].

References

  1. ↑ Dietz, Paul F. (1982), "Maintaining order in a linked list", Proceedings of the 14th Annual ACM Symposium on Theory of Computing (STOC '82), New York, NY, USA: ACM, pp. 122–127, doi:10.1145/800070.802184, ISBN 978-0897910705 .
  2. ↑ Tsakalidis, Athanasios K. (1984), "Maintaining order in a generalized linked list", Acta Informatica 21 (1): 101–112, doi:10.1007/BF00289142 .
  3. ↑ Dietz, P. (1987), "Two algorithms for maintaining order in a list", Proceedings of the 19th Annual ACM Symposium on Theory of Computing (STOC '87), New York, NY, USA: ACM, pp. 365–372, doi:10.1145/28395.28434, ISBN 978-0897912211 . Full version, Tech. Rep. CMU-CS-88-113, Carnegie Mellon University, 1988.
  4. ↑ Möhring, Rolf H.; Raman, Rajeev, eds. (2002), "Two simplified algorithms for maintaining order in a list", Algorithms – ESA 2002, 10th Annual European Symposium, Rome, Italy, September 17–21, 2002, Proceedings, Lecture Notes in Computer Science, 2461, Springer, pp. 152–164, doi:10.1007/3-540-45749-6_17 
  5. ↑ Klein, Philip N., ed. (2017), "File maintenance: When in doubt, change the layout!", Proceedings of the Twenty-Eighth Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2017, Barcelona, Spain, Hotel Porta Fira, January 16–19, Society for Industrial and Applied Mathematics, pp. 1503–1522, doi:10.1137/1.9781611974782.98 
  6. ↑ Driscoll, James R.; Sarnak, Neil (1989), "Making data structures persistent", Journal of Computer and System Sciences 38 (1): 86–124, doi:10.1016/0022-0000(89)90034-2 .
  7. ↑ "Sparsification—a technique for speeding up dynamic graph algorithms", Journal of the ACM 44 (5): 669–696, 1997, doi:10.1145/265910.265914 .
  8. ↑ Katriel, Irit (2006), "Online topological ordering", ACM Transactions on Algorithms 2 (3): 364–379, doi:10.1145/1159892.1159896 .
  9. ↑ Aumann, Yonatan; Bender, Michael A. (1996), "Fault tolerant data structures", Proceedings of the 37th Annual Symposium on Foundations of Computer Science (FOCS 1996), pp. 580–589, doi:10.1109/SFCS.1996.548517, ISBN 978-0-8186-7594-2 .
  10. ↑ Itai, Alon; Konheim, Alan G.; Rodeh, Michael (1981), "A Sparse Table Implementation of Priority Queues", ICALP, pp. 417-431 
  11. ↑ Bulánek, Jan; Koucký, Michal (2015), "Tight Lower Bounds for the Online Labeling Problem", SIAM Journal on Computing, 44, pp. 1765--1797 .

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Order-maintenance_problem&oldid=3385594"