Y-fast trie
| Y-fast trie | |||||
|---|---|---|---|---|---|
| Type | Trie | ||||
| Invented | 1982 | ||||
| Invented by | Dan Willard | ||||
| Time complexity in big O notation | |||||
| |||||
In computer science, a y-fast trie is a data structure for storing integers from a bounded domain. It supports exact and predecessor or successor queries in time O(log log M), using O(n) space, where n is the number of stored values and M is the maximum value in the domain. The structure was proposed by Dan Willard in 1982[1] to decrease the O(n log M) space used by an x-fast trie.
Structure
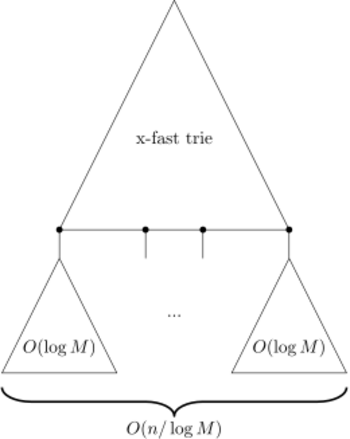
A y-fast trie consists of two data structures: the top half is an x-fast trie and the lower half consists of a number of balanced binary trees. The keys are divided into groups of O(log M) consecutive elements and for each group a balanced binary search tree is created. To facilitate efficient insertion and deletion, each group contains at least (log M)/4 and at most 2 log M elements.[2] For each balanced binary search tree a representative r is chosen. These representatives are stored in the x-fast trie. A representative r need not be an element of the tree associated with it, but it does need be an integer smaller than the successor of r and the minimum element of the tree associated with that successor and greater than the predecessor of r and the maximum element of the tree associated with that predecessor. Initially, the representative of a tree will be an integer between the minimum and maximum element in its tree.
Since the x-fast trie stores O(n / log M) representatives and each representative occurs in O(log M) hash tables, this part of the y-fast trie uses O(n) space. The balanced binary search trees store n elements in total which uses O(n) space. Hence, in total a y-fast trie uses O(n) space.
Operations
Like van Emde Boas trees and x-fast tries, y-fast tries support the operations of an ordered associative array. This includes the usual associative array operations, along with two more order operations, Successor and Predecessor:
- Find(k): find the value associated with the given key
- Successor(k): find the key/value pair with the smallest key larger than or equal to the given key
- Predecessor(k): find the key/value pair with the largest key less than or equal to the given key
- Insert(k, v): insert the given key/value pair
- Delete(k): remove the key/value pair with the given key
Find
A key k can be stored in either the tree of the smallest representative r greater than k or in the tree of the predecessor of r since the representative of a binary search tree need not be an element stored in its tree. Hence, one first finds the smallest representative r greater than k in the x-fast trie. Using this representative, one retrieves the predecessor of r. These two representatives point to two balanced binary search trees, both of which one searches for k.
Finding the smallest representative r greater than k in the x-fast trie takes O(log log M). Using r, finding its predecessor takes constant time. Searching the two balanced binary search trees containing O(log M) elements each takes O(log log M) time. Hence, a key k can be found, and its value retrieved, in O(log log M) time.[1]
Successor and Predecessor
Similarly to the key k itself, its successor can be stored in either the tree of the smallest representative r greater than k or in the tree of the predecessor of r. Hence, to find the successor of a key k, one first searches the x-fast trie for the smallest representative greater than k. Next, one uses this representative to retrieve its predecessor in the x-fast trie. These two representatives point to two balanced binary search trees, which one searches for the successor of k.[3]
Finding the smallest representative r greater than k in the x-fast trie takes O(log log M) time and using r to find its predecessor takes constant time. Searching the two balanced binary search trees containing O(log M) elements each takes O(log log M) time. Hence, the successor of a key k can be found, and its value retrieved, in O(log log M) time.[1]
Searching for the predecessor of a key k is highly similar to finding its successor. One searches the x-fast trie for the largest representative r smaller than k and one uses r to retrieve its predecessor in the x-fast trie. Finally, one searches the two balanced binary search trees of these two representatives for the predecessor of k. This takes O(log log M) time.
Insert
To insert a new key/value pair (k, v), one first needs to determine in which balanced binary search tree one needs to insert k. To this end, one finds the tree T containing the successor of k. Next, one inserts k into T. To ensure that all balanced binary search trees contain O(log M) elements, one splits T into two balanced binary trees and removes its representative from the x-fast trie if it contains more than 2 log M elements. Each of the two new balanced binary search trees contains at most log M + 1 elements. One picks a representative for each tree and insert these into the x-fast trie.
Finding the successor of k takes O(log log M) time. Inserting k into a balanced binary search tree that contains O(log M) elements also takes O(log log M) time. Splitting a binary search tree that contains O(log M) elements can be done in O(log log M) time. Finally, inserting and deleting the three representatives takes O(log M) time. However, since one splits the tree at most once every O(log M) insertions and deletions, this takes constant amortized time. Therefore, inserting a new key/value pair takes O(log log M) amortized time.[3]
Delete
Deletions are very similar to insertions. One first finds the key k in one of the balanced binary search trees and delete it from this tree T. To ensure that all balanced binary search trees contain O(log M) elements, one merges T with the balanced binary search tree of its successor or predecessor if it contains less than (log M)/4 elements. The representatives of the merged trees are removed from the x-fast trie. It is possible for the merged tree to contain more than 2 log M elements. If this is the case, the newly formed tree is split into two trees of about equal size. Next, one picks a new representative for each of the new trees and one inserts these into the x-fast trie.
Finding the key k takes O(log log M) time. Deleting k from a balanced binary search tree that contains O(log M) elements also takes O(log log M) time. Merging and possibly splitting the balanced binary search trees takes O(log log M) time. Finally, deleting the old representatives and inserting the new representatives into the x-fast trie takes O(log M) time. Merging and possibly splitting the balanced binary search tree, however, is done at most once for every O(log M) insertions and deletions. Hence, it takes constant amortized time. Therefore, deleting a key/value pair takes O(log log M) amortized time.[3]
References
- ↑ 1.0 1.1 1.2 Willard, Dan E. (1983). "Log-logarithmic worst-case range queries are possible in space Θ(N)". Information Processing Letters (Elsevier) 17 (2): 81–84. doi:10.1016/0020-0190(83)90075-3. ISSN 0020-0190.
- ↑ Bose; Douïeb, Karim; Dujmović; Howat, John; Morin (2010), Fast Local Searches and Updates in Bounded Universes, Proceedings of the 22nd Canadian Conference on Computational Geometry (CCCG2010), pp. 261–264, http://cccg.ca/proceedings/2010/paper69.pdf
- ↑ 3.0 3.1 3.2 Schulz, André; Christiano, Paul (2010-03-04). "Lecture Notes from Lecture 9 of Advanced Data Structures (Spring '10, 6.851)". http://courses.csail.mit.edu/6.851/spring10/scribe/lec09.pdf.
External links
 |  |
