Pancake sorting

Short description: Mathematics problem

Demonstration of the primary operation. The spatula is flipping over the top three pancakes, with the result seen below. In the burnt pancake problem, their top sides would now be burnt instead of their bottom sides.

Pancake sorting is the mathematical problem of sorting a disordered stack of pancakes in order of size when a spatula can be inserted at any point in the stack and used to flip all pancakes above it. A pancake number is the minimum number of flips required for a given number of pancakes. In this form, the problem was first discussed by American geometer Jacob E. Goodman. A variant of the problem is concerned with burnt pancakes, where each pancake has a burnt side and all pancakes must, in addition, end up with the burnt side on bottom.

All sorting methods require pairs of elements to be compared. For the traditional sorting problem, the usual problem studied is to minimize the number of comparisons required to sort a list. The number of actual operations, such as swapping two elements, is then irrelevant. For pancake sorting problems, in contrast, the aim is to minimize the number of operations, where the only allowed operations are reversals of the elements of some prefix of the sequence. Now, the number of comparisons is irrelevant.

The pancake problems

The original pancake problem

The minimum number of flips required to sort any stack of n pancakes has been shown to lie between 15/14n and 18/11n (approximately 1.07n and 1.64n), but the exact value is not known.

The simplest pancake sorting algorithm performs at most 2n − 3 flips. In this algorithm, a kind of selection sort, we bring the largest pancake not yet sorted to the top with one flip; take it down to its final position with one more flip; and repeat this process for the remaining pancakes.

In 1979, Bill Gates and Christos Papadimitriou gave a lower bound of 17/16n (approximately 1.06n) flips and an upper bound of (5n+5)/3. The upper bound was improved, thirty years later, to 18/11n by a team of researchers at the University of Texas at Dallas, led by Founders Professor Hal Sudborough.

In 2011, Laurent Bulteau, Guillaume Fertin, and Irena Rusu proved that the problem of finding the shortest sequence of flips for a given stack of pancakes is NP-hard, thereby answering a question that had been open for over three decades.

The burnt pancake problem

In a variation called the burnt pancake problem, the bottom of each pancake in the pile is burnt, and the sort must be completed with the burnt side of every pancake down. It is a signed permutation, and if a pancake i is "burnt side up" a negative element i` is put in place of i in the permutation. In 2008, a group of undergraduates built a bacterial computer that can solve a simple example of the burnt pancake problem by programming E. coli to flip segments of DNA which are analogous to burnt pancakes. DNA has an orientation (5' and 3') and an order (promoter before coding). Even though the processing power expressed by DNA flips is low, the high number of bacteria in a culture provides a large parallel computing platform. The bacteria report when they have solved the problem by becoming antibiotic resistant.

The identical pancakes stack problem

This is inspired from the way Indian bread (roti or chapati) is cooked. Initially, all rotis are stacked in one column, and the cook uses a spatula to flip the rotis so that each side of each roti touches the base fire at some point to toast. Several variants are possible: the rotis can be considered as single-sided or two-sided, and it may be forbidden or not to toast the same side twice. This version of the problem was first explored by Arka Roychowdhury.

The pancake problem on strings

The discussion above presumes that each pancake is unique, that is, the sequence on which the prefix reversals are performed is a permutation. However, "strings" are sequences in which a symbol can repeat, and this repetition may reduce the number of prefix reversals required to sort. Chitturi and Sudborough (2010) and Hurkens et al. (2007) independently showed that the complexity of transforming a compatible string into another with the minimum number of prefix reversals is NP-complete. They also gave bounds for the same. Hurkens et al. gave an exact algorithm to sort binary and ternary strings. Chitturi (2011) proved that the complexity of transforming a compatible signed string into another with the minimum number of signed prefix reversals—the burnt pancake problem on strings—is NP-complete.

History

The pancake sorting problem was first posed by Jacob E. Goodman, writing under the pseudonym "Harry Dweighter" ("harried waiter").

Although seen more often as an educational device, pancake sorting also appears in applications in parallel processor networks, in which it can provide an effective routing algorithm between processors.

The problem is notable as the topic of the only well-known mathematics paper by Microsoft founder Bill Gates (as William Gates), entitled "Bounds for Sorting by Prefix Reversal" and co-authored with Christos Papadimitriou. Published in 1979, it describes an efficient algorithm for pancake sorting. In addition, the most notable paper published by Futurama co-creator David X. Cohen (as David S. Cohen), co-authored with Manuel Blum, concerned the burnt pancake problem.

The connected problems of signed sorting by reversals and sorting by reversals were also studied more recently. Whereas efficient exact algorithms have been found for the signed sorting by reversals, the problem of sorting by reversals has been proven to be hard even to approximate to within certain constant factor, and also proven to be approximable in polynomial time to within the approximation factor 1.375.

Pancake graphs

The pancake graph P₃

The pancake graph P₄ can be constructed recursively from 4 copies of P₃ by assigning a different element from the set {1, 2, 3, 4} as a suffix to each copy.

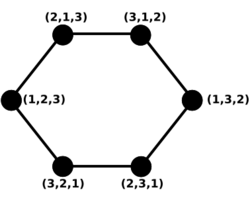
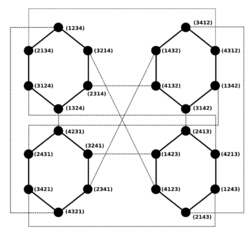
An n-pancake graph is a graph whose vertices are the permutations of n symbols from 1 to n and its edges are given between permutations transitive by prefix reversals. It is a regular graph with n! vertices, its degree is n−1. The pancake sorting problem and the problem to obtain the diameter of the pancake graph is equivalent.

The pancake graph of dimension n, P_n can be constructed recursively from n copies of P_n−1, by assigning a different element from the set {1, 2, …, n} as a suffix to each copy.

Their girth:

[math]\displaystyle{ g(P_n) = 6 \text{, if } n\gt 2 }[/math].

The γ(P_n) genus of P_n is:

[math]\displaystyle{ n!\left( \frac{n-4}{6} \right)+1 \le \gamma(P_n) \le n!\left( \frac{n-3}{4} \right)-\frac{n}{2}+1 }[/math]

Since pancake graphs have many interesting properties such as symmetric and recursive structures, small degrees and diameters compared against the size of the graph, much attention is paid to them as a model of interconnection networks for parallel computers. When we regard the pancake graphs as the model of the interconnection networks, the diameter of the graph is a measure that represents the delay of communication.

The pancake graphs are Cayley graphs (thus are vertex-transitive) and are especially attractive for parallel processing. They have sublogarithmic degree and diameter, and are relatively sparse (compared to e.g. hypercubes).

Algorithm

An example of the pancake sorting algorithm is given below in Python. The code is similar to bubble sort or selection sort.

def flip(arr, k: int) -> None:
    left = 0
    while left < k:
        arr[left], arr[k] = arr[k], arr[left]
        k -= 1
        left += 1

def max_index(arr, k: int) -> int:
    index = 0
    for i in range(k):
        if arr[i] > arr[index]:
            index = i
    return index

def pancake_sort(arr) -> None:
    n = len(arr)
    while n > 1:
        maxdex = max_index(arr, n)
        if maxdex != n - 1:
            if maxdex != 0:
                flip(arr, maxdex)
            flip(arr, n - 1)
        n -= 1

arreglo = [15, 8, 9, 1, 78, 30, 69, 4, 10]
pancake_sort(arreglo)
print(arreglo)

Related integer sequences

Number of stacks of given height n that require unique flips k  to get sorted

Height n	k
	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	1
2	1	1
3	1	2	2	1
4	1	3	6	11	3
5	1	4	12	35	48	20
6	1	5	20	79	199	281	133	2
7	1	6	30	149	543	1357	1903	1016	35
8	1	7	42	251	1191	4281	10561	15011	8520	455
9	1	8	56	391	2278	10666	38015	93585	132697	79379	5804
10	1	9	72	575	3963	22825	106461	377863	919365	1309756	814678	73232
11	1	10	90	809	6429	43891	252737	1174766	4126515	9981073	14250471	9123648	956354	6
12	1	11	110	1099	9883	77937	533397	3064788	14141929	49337252	118420043	169332213	111050066	13032704	167
13	1	12	132	1451	14556	130096	1030505	7046321	40309555	184992275	639783475	1525125357	2183056566	1458653648	186874852	2001

Sequences from The Online Encyclopedia of Integer Sequences:

• OEIS: A058986 – maximum number of flips
• OEIS: A067607 – number of stacks requiring the maximum number of flips (above)
• OEIS: A078941 – maximum number of flips for a "burnt" stack
• OEIS: A078942 – the number of flips for a sorted "burnt-side-on-top" stack
• OEIS: A092113 – the above triangle, read by rows

Further reading

• Chitturi, B.; Sudborough, H. (2010). "Prefix Reversals on Strings". Proceedings of the International Conference on Bioinformatics & Computational Biology 2: 591–598. https://www.researchgate.net/publication/221051667. 
• Chitturi, B. (2011). "A Note on Complexity of Genetic Mutations". Discrete Math. Algorithm. Appl. 3 (3): 269–287. doi:10.1142/S1793830911001206. 
• Heydari, M. H.; Sudborough, I. H. (1997). "On the Diameter of the Pancake Network". Journal of Algorithms 25 (1): 67–94. doi:10.1006/jagm.1997.0874. 
• Hurkens, C.; van Iersel, L.; Keijsper, J.; Kelk, S.; Stougie, L.; Tromp, J. (2007). "Prefix Reversals on Binary and Ternary Strings". SIAM Journal on Discrete Mathematics 21 (3): 592–611. doi:10.1137/060664252. 
• Roney-Dougal, C.; Vatter, V. (March 2010). "Of Pancakes, Mice and Men". Plus Magazine 54. http://plus.maths.org/issue54/features/colvatter/. 

External links

• Cut-the-Knot: Flipping pancakes puzzle, including a Java applet for the pancake problem and some discussion.
• Douglas B. West's "The Pancake Problems"
• Weisstein, Eric W.. "Pancake Sorting". http://mathworld.wolfram.com/PancakeSorting.html. 
• Animation explaining the bacterial computer that can solve the burnt pancake problem.
• "Tower1/Pancake Flip" by Arka. A game based on pancake problem principle