Panjer recursion

The Panjer recursion is an algorithm to compute the probability distribution approximation of a compound random variable [math]\displaystyle{ S = \sum_{i=1}^N X_i\, }[/math] where both [math]\displaystyle{ N\, }[/math] and [math]\displaystyle{ X_i\, }[/math] are random variables and of special types. In more general cases the distribution of S is a compound distribution. The recursion for the special cases considered was introduced in a paper by Harry Panjer (Distinguished Emeritus Professor, University of Waterloo). It is heavily used in actuarial science (see also systemic risk).

Preliminaries

We are interested in the compound random variable [math]\displaystyle{ S = \sum_{i=1}^N X_i\, }[/math] where [math]\displaystyle{ N\, }[/math] and [math]\displaystyle{ X_i\, }[/math] fulfill the following preconditions.

Claim size distribution

We assume the [math]\displaystyle{ X_i\, }[/math] to be i.i.d. and independent of [math]\displaystyle{ N\, }[/math]. Furthermore the [math]\displaystyle{ X_i\, }[/math] have to be distributed on a lattice [math]\displaystyle{ h \mathbb{N}_0\, }[/math] with latticewidth [math]\displaystyle{ h\gt 0\, }[/math].

[math]\displaystyle{ f_k = P[X_i = hk].\, }[/math]

In actuarial practice, [math]\displaystyle{ X_i\, }[/math] is obtained by discretisation of the claim density function (upper, lower...).

Claim number distribution

The number of claims N is a random variable, which is said to have a "claim number distribution", and which can take values 0, 1, 2, .... etc.. For the "Panjer recursion", the probability distribution of N has to be a member of the Panjer class, otherwise known as the (a,b,0) class of distributions. This class consists of all counting random variables which fulfill the following relation:

[math]\displaystyle{ P[N=k] = p_k= \left(a + \frac{b}{k} \right) \cdot p_{k-1},~~k \ge 1.\, }[/math]

for some [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] which fulfill [math]\displaystyle{ a+b \ge 0\, }[/math]. The initial value [math]\displaystyle{ p_0\, }[/math] is determined such that [math]\displaystyle{ \sum_{k=0}^\infty p_k = 1.\, }[/math]

The Panjer recursion makes use of this iterative relationship to specify a recursive way of constructing the probability distribution of S. In the following [math]\displaystyle{ W_N(x)\, }[/math] denotes the probability generating function of N: for this see the table in (a,b,0) class of distributions.

In the case of claim number is known, please note the De Pril algorithm. This algorithm is suitable to compute the sum distribution of [math]\displaystyle{ n }[/math] discrete random variables.

Recursion

The algorithm now gives a recursion to compute the [math]\displaystyle{ g_k =P[S = hk] \, }[/math].

The starting value is [math]\displaystyle{ g_0 = W_N(f_0)\, }[/math] with the special cases

[math]\displaystyle{ g_0=p_0\cdot \exp(f_0 b) \quad \text{ if } \quad a = 0,\, }[/math]

and

[math]\displaystyle{ g_0=\frac{p_0}{(1-f_0a)^{1+b/a}} \quad \text{ for } \quad a \ne 0,\, }[/math]

and proceed with

[math]\displaystyle{ g_k=\frac{1}{1-f_0a}\sum_{j=1}^k \left( a+\frac{b\cdot j}{k} \right) \cdot f_j \cdot g_{k-j}.\, }[/math]

Example

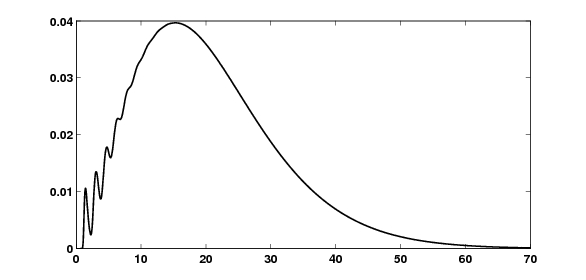
The following example shows the approximated density of [math]\displaystyle{ \scriptstyle S \,=\, \sum_{i=1}^N X_i }[/math] where [math]\displaystyle{ \scriptstyle N\, \sim\, \text{NegBin}(3.5,0.3)\, }[/math] and [math]\displaystyle{ \scriptstyle X \,\sim \,\text{Frechet}(1.7,1) }[/math] with lattice width h = 0.04. (See Fréchet distribution.)

As observed, an issue may arise at the initialization of the recursion. Guégan and Hassani (2009) have proposed a solution to deal with that issue .

External links

• Panjer recursion and the distributions it can be used with