Pappus's hexagon theorem

Short description: Geometry theorem

Pappus's hexagon theorem: Points X, Y and Z are collinear on the Pappus line. The hexagon is AbCaBc.

Pappus's theorem: affine form
[math]\displaystyle{ Ab\parallel aB, Bc\parallel bC \Rightarrow Ac\parallel aC }[/math]

In mathematics, Pappus's hexagon theorem (attributed to Pappus of Alexandria) states that

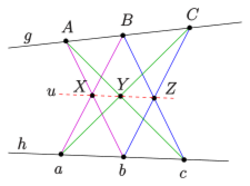
• given one set of collinear points [math]\displaystyle{ A, B, C, }[/math] and another set of collinear points [math]\displaystyle{ a,b,c, }[/math] then the intersection points [math]\displaystyle{ X,Y,Z }[/math] of line pairs [math]\displaystyle{ Ab }[/math] and [math]\displaystyle{ aB, Ac }[/math] and [math]\displaystyle{ aC, Bc }[/math] and [math]\displaystyle{ bC }[/math] are collinear, lying on the Pappus line. These three points are the points of intersection of the "opposite" sides of the hexagon [math]\displaystyle{ AbCaBc }[/math].

It holds in a projective plane over any field, but fails for projective planes over any noncommutative division ring. Projective planes in which the "theorem" is valid are called pappian planes.

If one restricts the projective plane such that the Pappus line [math]\displaystyle{ u }[/math] is the line at infinity, one gets the affine version of Pappus's theorem shown in the second diagram.

If the Pappus line [math]\displaystyle{ u }[/math] and the lines [math]\displaystyle{ g,h }[/math] have a point in common, one gets the so-called little version of Pappus's theorem.

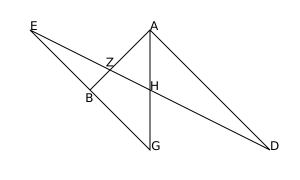
The dual of this incidence theorem states that given one set of concurrent lines [math]\displaystyle{ A, B, C }[/math], and another set of concurrent lines [math]\displaystyle{ a, b, c }[/math], then the lines [math]\displaystyle{ x, y, z }[/math] defined by pairs of points resulting from pairs of intersections [math]\displaystyle{ A\cap b }[/math] and [math]\displaystyle{ a\cap B, \; A\cap c }[/math] and [math]\displaystyle{ a\cap C, \;B\cap c }[/math] and [math]\displaystyle{ b\cap C }[/math] are concurrent. (Concurrent means that the lines pass through one point.)

Pappus's theorem is a special case of Pascal's theorem for a conic—the limiting case when the conic degenerates into 2 straight lines. Pascal's theorem is in turn a special case of the Cayley–Bacharach theorem.

The Pappus configuration is the configuration of 9 lines and 9 points that occurs in Pappus's theorem, with each line meeting 3 of the points and each point meeting 3 lines. In general, the Pappus line does not pass through the point of intersection of [math]\displaystyle{ ABC }[/math] and [math]\displaystyle{ abc }[/math]. This configuration is self dual. Since, in particular, the lines [math]\displaystyle{ Bc, bC, XY }[/math] have the properties of the lines [math]\displaystyle{ x,y,z }[/math] of the dual theorem, and collinearity of [math]\displaystyle{ X,Y,Z }[/math] is equivalent to concurrence of [math]\displaystyle{ Bc, bC, XY }[/math], the dual theorem is therefore just the same as the theorem itself. The Levi graph of the Pappus configuration is the Pappus graph, a bipartite distance-regular graph with 18 vertices and 27 edges.

Proof: affine form

Pappus theorem: proof

If the affine form of the statement can be proven, then the projective form of Pappus's theorem is proven, as the extension of a pappian plane to a projective plane is unique.

Because of the parallelity in an affine plane one has to distinct two cases: [math]\displaystyle{ g \not\parallel h }[/math] and [math]\displaystyle{ g \parallel h }[/math]. The key for a simple proof is the possibility for introducing a "suitable" coordinate system:

Case 1: The lines [math]\displaystyle{ g,h }[/math] intersect at point [math]\displaystyle{ S=g\cap h }[/math].
In this case coordinates are introduced, such that [math]\displaystyle{ \;S=(0,0), \; A=(0,1), \;c=(1,0)\; }[/math] (see diagram). [math]\displaystyle{ B,C }[/math] have the coordinates [math]\displaystyle{ \;B=(0,\gamma),\; C=(0,\delta), \; \gamma,\delta \notin \{0,1\} }[/math].

From the parallelity of the lines [math]\displaystyle{ Bc,\; Cb }[/math] one gets [math]\displaystyle{ b=(\tfrac{\delta}{\gamma},0) }[/math] and the parallelity of the lines [math]\displaystyle{ Ab, Ba }[/math] yields [math]\displaystyle{ a=(\delta,0) }[/math]. Hence line [math]\displaystyle{ Ca }[/math] has slope [math]\displaystyle{ -1 }[/math] and is parallel line [math]\displaystyle{ Ac }[/math].

Case 2: [math]\displaystyle{ g\parallel h \ }[/math] (little theorem).
In this case the coordinates are chosen such that [math]\displaystyle{ \;c=(0,0), \;b=(1,0),\; A=(0,1), \;B=(\gamma,1),\;\gamma\ne 0 }[/math]. From the parallelity of [math]\displaystyle{ Ab\parallel Ba }[/math] and [math]\displaystyle{ cB\parallel bC }[/math] one gets [math]\displaystyle{ \;C=(\gamma+1,1)\; }[/math] and [math]\displaystyle{ \;a=(\gamma+1,0)\; }[/math], respectively, and at least the parallelity [math]\displaystyle{ \;Ac\parallel Ca\; }[/math].

Proof with homogeneous coordinates

Choose homogeneous coordinates with

[math]\displaystyle{ C = (1, 0, 0), \; c= (0, 1, 0),\; X = (0, 0, 1), \; A = (1, 1, 1) }[/math].

On the lines [math]\displaystyle{ AC, Ac, AX }[/math], given by [math]\displaystyle{ x_2 = x_3,\; x_1 =x_3, \; x_2 = x_1 }[/math], take the points [math]\displaystyle{ B, Y, b }[/math] to be

[math]\displaystyle{ B = (p, 1, 1),\; Y = (1, q, 1),\; b = (1, 1, r) }[/math]

for some [math]\displaystyle{ p, q, r }[/math]. The three lines [math]\displaystyle{ XB, CY, cb }[/math] are [math]\displaystyle{ x_1 = x_2 p,\; x_2= x_3 q,\; x_3 = x_1 r }[/math], so they pass through the same point [math]\displaystyle{ a }[/math] if and only if [math]\displaystyle{ rqp = 1 }[/math]. The condition for the three lines [math]\displaystyle{ Cb, cB }[/math] and [math]\displaystyle{ XY }[/math] with equations [math]\displaystyle{ x_2 = x_1 q,\; x_1 = x_3 p ,\; x_3 = x_2 r }[/math] to pass through the same point [math]\displaystyle{ Z }[/math] is [math]\displaystyle{ rpq =1 }[/math]. So this last set of three lines is concurrent if all the other eight sets are because multiplication is commutative, so [math]\displaystyle{ pq = qp }[/math]. Equivalently, [math]\displaystyle{ X, Y, Z }[/math] are collinear.

The proof above also shows that for Pappus's theorem to hold for a projective space over a division ring it is both sufficient and necessary that the division ring is a (commutative) field. German mathematician Gerhard Hessenberg proved that Pappus's theorem implies Desargues's theorem. In general, Pappus's theorem holds for some projective plane if and only if it is a projective plane over a commutative field. The projective planes in which Pappus's theorem does not hold are Desarguesian projective planes over noncommutative division rings, and non-Desarguesian planes.

The proof is invalid if [math]\displaystyle{ C, c, X }[/math] happen to be collinear. In that case an alternative proof can be provided, for example, using a different projective reference.

Dual theorem

Because of the principle of duality for projective planes the dual theorem of Pappus is true:

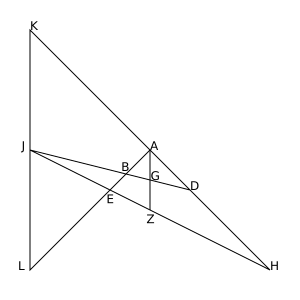
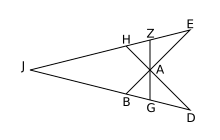
If 6 lines [math]\displaystyle{ A,b,C,a,B,c }[/math] are chosen alternately from two pencils with centers [math]\displaystyle{ G,H }[/math], the lines

[math]\displaystyle{ X:= (A\cap b) (a\cap B), }[/math]

[math]\displaystyle{ Y:= (c\cap A) (C\cap a), }[/math]

[math]\displaystyle{ Z:= (b\cap C) (B\cap c) }[/math]

are concurrent, that means: they have a point [math]\displaystyle{ U }[/math] in common.
The left diagram shows the projective version, the right one an affine version, where the points [math]\displaystyle{ G,H }[/math] are points at infinity. If point [math]\displaystyle{ U }[/math] is on the line [math]\displaystyle{ GH }[/math] than one gets the "dual little theorem" of Pappus' theorem.

• 

  dual theorem: projective form

• 

  dual theorem: affine form

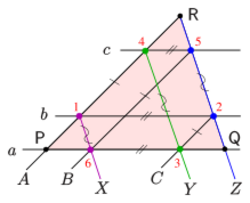
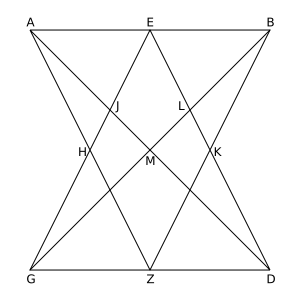
If in the affine version of the dual "little theorem" point [math]\displaystyle{ U }[/math] is a point at infinity too, one gets Thomsen's theorem, a statement on 6 points on the sides of a triangle (see diagram). The Thomsen figure plays an essential role coordinatising an axiomatic defined projective plane. The proof of the closure of Thomsen's figure is covered by the proof for the "little theorem", given above. But there exists a simple direct proof, too:

Because the statement of Thomsen's theorem (the closure of the figure) uses only the terms connect, intersect and parallel, the statement is affinely invariant, and one can introduce coordinates such that [math]\displaystyle{ P=(0,0), \; Q=(1,0), \; R=(0,1) }[/math] (see right diagram). The starting point of the sequence of chords is [math]\displaystyle{ (0,\lambda). }[/math] One easily verifies the coordinates of the points given in the diagram, which shows: the last point coincides with the first point.

• 

  Thomsen figure (points [math]\displaystyle{ \color{red} 1,2,3,4,5,6 }[/math] of the triangle [math]\displaystyle{ PQR }[/math]) as dual theorem of the little theorem of Pappus ([math]\displaystyle{ U }[/math] is at infinity, too !).

• 

  Thomsen figure: proof

Other statements of the theorem

Triangles [math]\displaystyle{ XcC }[/math] and [math]\displaystyle{ BbY }[/math] are perspective from [math]\displaystyle{ A }[/math] and [math]\displaystyle{ a }[/math], and so, also from [math]\displaystyle{ Z }[/math].

In addition to the above characterizations of Pappus's theorem and its dual, the following are equivalent statements:

• If the six vertices of a hexagon lie alternately on two lines, then the three points of intersection of pairs of opposite sides are collinear.
• Arranged in a matrix of nine points (as in the figure and description above) and thought of as evaluating a permanent, if the first two rows and the six "diagonal" triads are collinear, then the third row is collinear.

[math]\displaystyle{ \left|\begin{matrix} A & B & C \\ a & b & c \\ X & Y & Z \end{matrix} \right| }[/math]

That is, if [math]\displaystyle{ \ ABC, abc, AbZ, BcX, CaY, XbC, YcA, ZaB\ }[/math] are lines, then Pappus's theorem states that [math]\displaystyle{ XYZ }[/math] must be a line. Also, note that the same matrix formulation applies to the dual form of the theorem when [math]\displaystyle{ (A,B,C) }[/math] etc. are triples of concurrent lines.

• Given three distinct points on each of two distinct lines, pair each point on one of the lines with one from the other line, then the joins of points not paired will meet in (opposite) pairs at points along a line.
• If two triangles are perspective in at least two different ways, then they are perspective in three ways.
• If [math]\displaystyle{ \; AB, CD,\; }[/math] and [math]\displaystyle{ EF }[/math] are concurrent and [math]\displaystyle{ DE, FA, }[/math] and [math]\displaystyle{ BC }[/math] are concurrent, then [math]\displaystyle{ AD, BE, }[/math] and [math]\displaystyle{ CF }[/math] are concurrent.

Origins

In its earliest known form, Pappus's Theorem is Propositions 138, 139, 141, and 143 of Book VII of Pappus's Collection. These are Lemmas XII, XIII, XV, and XVII in the part of Book VII consisting of lemmas to the first of the three books of Euclid's Porisms.

The lemmas are proved in terms of what today is known as the cross ratio of four collinear points. Three earlier lemmas are used. The first of these, Lemma III, has the diagram below (which uses Pappus's lettering, with G for Γ, D for Δ, J for Θ, and L for Λ).

Here three concurrent straight lines, AB, AG, and AD, are crossed by two lines, JB and JE, which concur at J. Also KL is drawn parallel to AZ. Then

KJ : JL :: (KJ : AG & AG : JL) :: (JD : GD & BG : JB).

These proportions might be written today as equations:

KJ/JL = (KJ/AG)(AG/JL) = (JD/GD)(BG/JB).

The last compound ratio (namely JD : GD & BG : JB) is what is known today as the cross ratio of the collinear points J, G, D, and B in that order; it is denoted today by (J, G; D, B). So we have shown that this is independent of the choice of the particular straight line JD that crosses the three straight lines that concur at A. In particular

(J, G; D, B) = (J, Z; H, E).

It does not matter on which side of A the straight line JE falls. In particular, the situation may be as in the next diagram, which is the diagram for Lemma X.

Just as before, we have (J, G; D, B) = (J, Z; H, E). Pappus does not explicitly prove this; but Lemma X is a converse, namely that if these two cross ratios are the same, and the straight lines BE and DH cross at A, then the points G, A, and Z must be collinear.

What we showed originally can be written as (J, ∞; K, L) = (J, G; D, B), with ∞ taking the place of the (nonexistent) intersection of JK and AG. Pappus shows this, in effect, in Lemma XI, whose diagram, however, has different lettering:

What Pappus shows is DE.ZH : EZ.HD :: GB : BE, which we may write as

(D, Z; E, H) = (∞, B; E, G).

The diagram for Lemma XII is:

The diagram for Lemma XIII is the same, but BA and DG, extended, meet at N. In any case, considering straight lines through G as cut by the three straight lines through A, (and accepting that equations of cross ratios remain valid after permutation of the entries,) we have by Lemma III or XI

(G, J; E, H) = (G, D; ∞ Z).

Considering straight lines through D as cut by the three straight lines through B, we have

(L, D; E, K) = (G, D; ∞ Z).

Thus (E, H; J, G) = (E, K; D, L), so by Lemma X, the points H, M, and K are collinear. That is, the points of intersection of the pairs of opposite sides of the hexagon ADEGBZ are collinear.

Lemmas XV and XVII are that, if the point M is determined as the intersection of HK and BG, then the points A, M, and D are collinear. That is, the points of intersection of the pairs of opposite sides of the hexagon BEKHZG are collinear.

References

• Coxeter, Harold Scott MacDonald (1969), Introduction to Geometry (2nd ed.), New York: John Wiley & Sons, ISBN 978-0-471-50458-0 
• Cronheim, A. (1953), "A proof of Hessenberg's theorem", Proceedings of the American Mathematical Society 4 (2): 219–221, doi:10.2307/2031794 
• Dembowski, Peter (1968), Finite Geometries, Berlin: Springer-Verlag 
• Heath, Thomas (1981), A History of Greek Mathematics, New York: Dover Publications 
• Hessenberg, Gerhard (1905), "Beweis des Desarguesschen Satzes aus dem Pascalschen", Mathematische Annalen (Berlin / Heidelberg: Springer) 61 (2): 161–172, doi:10.1007/BF01457558, ISSN 1432-1807 
• Hultsch, Fridericus (1877), Pappi Alexandrini Collectionis Quae Supersunt, Berlin 
• Kline, Morris (1972), Mathematical Thought From Ancient to Modern Times, New York: Oxford University Press 
• Pambuccian, Victor; Schacht, Celia (2019), "The axiomatic destiny of the theorems of Pappus and Desargues", in Dani, S. G.; Papadopoulos, A., Geometry in history, Springer, pp. 355–399, ISBN 978-3-030-13611-6 
• Whicher, Olive (1971), Projective Geometry, Rudolph Steiner Press, ISBN 0-85440-245-4 

External links

• Pappus's hexagon theorem at cut-the-knot
• Dual to Pappus's hexagon theorem at cut-the-knot
• Pappus’s Theorem: Nine proofs and three variations