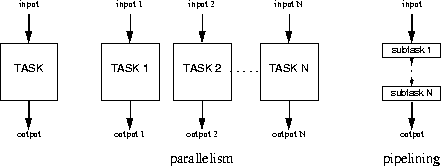
Parallel processing

Modern real-time digital signal and image processing operations have a tendency of being highly compute-intensive. Speedups of many orders of magnitude over previous systems were found through improvements in new technologies, e.g. integrated circuits; also improving algorithms and programming techniques have contributed. A major gain also comes from parallel computer architectures, interconnected commodity processors with programs using parallelism and pipelining at different levels.

For some applications, such architectures can improve overall speed substantially. Minsky expected only a increase in speedup by bus-oriented multiprocessor architectures; supercomputer architects claimed an increase according to Amdahl's formula (but see also Amdahl's law concerning general gains in parallelism). H.T. Kung claims ( Kung79) a perfectly linear speedup for his systolic array architecture. Clearly, we are in a domain of conjectures (and hype), and except for specific applications, nothing general can be stated. Most recently, it seems that the market favours clusters of general-purpose processors, with connections programmable as a shared-memory or message passing paradigm; they seem to dominate other architectures economically, even if applications lend themselves readily to finer-grain parallelism and better adapted architectures.

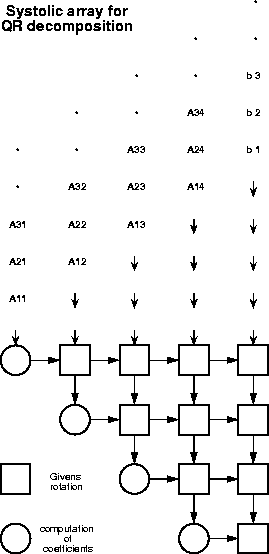
Systolic arrays are one- to three-dimensional arrays of simple, mostly identical processing elements, with nearest-neighbour connection. They both compute and pass data rhythmically through the system (the word ``systole is used in physiology, describing the rhythmical pulses of blood through the body).

An example of the use of systolic arrays is the implementation of the solution of the general linear least squares problem

with the known matrix A(m,n) and vector b(m), and the unknown vector x(n). Usually m>n. If we used the orthogonal triangularization A = QR by the Givens rotation, we could use the following systolic architecture (derived in Gentleman81) to perform the QR decomposition, and a linear one for the backsubstitution .

In the figure, circles correspond to computation of the coefficients of the Givens rotation, and the squares perform the rotation. In McWhirter83 a systolic architecture is described that produces immediately the residuals of such a fit. Because of problems connected with synchronization of a large array of processors, the asynchronous data-driven wave-array processor is usually preferred. It has the same structure as a systolic array, but without a global clock. Not correct timing, but only correct sequencing is important.

For more reading and more references, Kung88, Bromley86, Whitehouse85.