Perifocal coordinate system
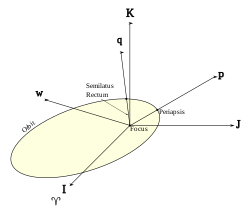
The perifocal coordinate (PQW) system is a frame of reference for an orbit. The frame is centered at the focus of the orbit, i.e. the celestial body about which the orbit is centered. The unit vectors [math]\displaystyle{ \mathbf{\hat{p}} }[/math] and [math]\displaystyle{ \mathbf{\hat{q}} }[/math] lie in the plane of the orbit. [math]\displaystyle{ \mathbf{\hat{p}} }[/math] is directed towards the periapsis of the orbit and [math]\displaystyle{ \mathbf{\hat{q}} }[/math] has a true anomaly ([math]\displaystyle{ \theta }[/math]) of 90 degrees past the periapsis. The third unit vector [math]\displaystyle{ \mathbf{\hat{w}} }[/math] is the angular momentum vector and is directed orthogonal to the orbital plane such that:[1][2] [math]\displaystyle{ \mathbf{\hat{w}} = \mathbf{\hat{p}} \times \mathbf{\hat{q}} }[/math]
And, since [math]\displaystyle{ \mathbf{\hat{w}} }[/math] is the unit vector in the direction of the angular momentum vector, it may also be expressed as: [math]\displaystyle{ \mathbf{\hat{w}} = \frac{\mathbf{h}}{\|\mathbf{h}\|} }[/math] where h is the specific relative angular momentum.
The position and velocity vectors can be determined for any location of the orbit. The position vector, r, can be expressed as: [math]\displaystyle{ \mathbf{r} = r \cos \theta \mathbf{\hat{p}} + r \sin \theta \mathbf{\hat{q}} }[/math] where [math]\displaystyle{ \theta }[/math] is the true anomaly and the radius [math]\displaystyle{ r = \|\mathbf{r}\| }[/math] may be calculated from the orbit equation.
The velocity vector, v, is found by taking the time derivative of the position vector: [math]\displaystyle{ \mathbf{v} = \mathbf{\dot{r}} = (\dot{r} \cos \theta - r \dot{\theta} \sin \theta)\mathbf{\hat{p}} + (\dot{r} \sin \theta + r \dot{\theta} \cos \theta)\mathbf{\hat{q}} }[/math]
A derivation from the orbit equation can be made to show that: [math]\displaystyle{ \dot{r} = \frac{\mu}{h}e \sin \theta }[/math] where [math]\displaystyle{ \mu }[/math] is the gravitational parameter of the focus, h is the specific relative angular momentum of the orbital body, e is the eccentricity of the orbit, and [math]\displaystyle{ \theta }[/math] is the true anomaly. [math]\displaystyle{ \dot{r} }[/math] is the radial component of the velocity vector (pointing inward toward the focus) and [math]\displaystyle{ r \dot{\theta} }[/math] is the tangential component of the velocity vector. By substituting the equations for [math]\displaystyle{ \dot{r} }[/math] and [math]\displaystyle{ r \dot{\theta} }[/math] into the velocity vector equation and simplifying, the final form of the velocity vector equation is obtained as:[3] [math]\displaystyle{ \mathbf{v} = \frac{\mu}{h} \left[-\sin \theta \mathbf{\hat{p}} + (e + \cos \theta) \mathbf{\hat{q}}\right] }[/math]
Conversion between coordinate systems
The perifocal coordinate system can also be defined using the orbital parameters inclination (i), right ascension of the ascending node ([math]\displaystyle{ \Omega }[/math]) and the argument of periapsis ([math]\displaystyle{ \omega }[/math]). The following equations convert from perifocal coordinates to equatorial coordinates and vice versa.[4]
Perifocal to equatorial
[math]\displaystyle{ \begin{bmatrix} x_\text{equatorial} \\ y_\text{equatorial} \\ z_\text{equatorial} \\ \end{bmatrix} = \begin{bmatrix} \cos\Omega\cos\omega - \sin\Omega\cos i\sin\omega & -\cos\Omega\sin\omega - \sin\Omega\cos i\cos \omega & \sin\Omega \sin i \\ \sin\Omega\cos\omega + \cos\Omega\cos i\sin\omega & -\sin\Omega\sin\omega + \cos\Omega\cos i\cos\omega & -\cos \Omega \sin i \\ \sin i \sin\omega & \sin i \cos\omega & \cos i \\ \end{bmatrix} \begin{bmatrix} x_\text{perifocal} \\ y_\text{perifocal} \\ z_\text{perifocal} \\ \end{bmatrix} }[/math]
In most cases, [math]\displaystyle{ z_\text{perifocal} = 0 }[/math].
Equatorial to perifocal
[math]\displaystyle{ \begin{bmatrix} x_\text{perifocal} \\ y_\text{perifocal} \\ z_\text{perifocal} \\ \end{bmatrix} = \begin{bmatrix} \cos\Omega\cos\omega - \sin\Omega\cos i\sin\omega & \sin\Omega\cos\omega + \cos\Omega\cos i\sin\omega & \sin i \sin\omega \\ -\cos\Omega\sin\omega - \sin\Omega\cos i\cos\omega & -\sin\Omega\sin\omega + \cos\Omega\cos i\cos\omega & \sin i \cos\omega \\ \sin\Omega \sin i & -\cos \Omega \sin i & \cos i \\ \end{bmatrix} \begin{bmatrix} x_\text{equatorial} \\ y_\text{equatorial} \\ z_\text{equatorial} \\ \end{bmatrix} }[/math]
Applications
Perifocal reference frames are most commonly used with elliptical orbits for the reason that the [math]\displaystyle{ \mathbf{\hat{p}} }[/math] coordinate must be aligned with the eccentricity vector. Circular orbits, having no eccentricity, give no means by which to orient the coordinate system about the focus.[5]
The perifocal coordinate system may also be used as an inertial frame of reference because the axes do not rotate relative to the fixed stars. This allows the inertia of any orbital bodies within this frame of reference to be calculated. This is useful when attempting to solve problems like the two-body problem.[6]
References
- ↑ 2011 Mathematics Clinic. (2011). Optimal Collison Avoidance of Operational Spacecraft in Near-Real Time. Denver, Colorado: University of Colorado, Denver.
- ↑ Seefelder, W. (2002). Lunar Transfer Orbits utilizing Solar Perturbations and Ballistic Capture. Munich, Germany. pg 12
- ↑ Curtis, H. D. (2005). Orbital Mechanics for Engineering Students. Burlington, MA: Elsevier Buttersorth-Heinemann. pp 76–77
- ↑ Curtis, H. D. (2005). Orbital Mechanics for Engineering Students. Burlington, MA: Elsevier Buttersorth-Heinemann. pp 174
- ↑ Karr, C. L., & Freeman, L. M. (1999). Industrial Applications of Genetic Algorithms. Danvers, MA. pg 142
- ↑ Vallado, D. A. (2001). Fundamentals of Astrodynamics and Applications. els Segundo, CA: Microcosm Press. pp 161–162
 |  |
