Pfaffian constraint
In dynamics, a Pfaffian constraint is a way to describe a dynamical system in the form:
where is the number of equations in a system of constraints, and are functions of only. In other words, it is a 1-form on .
Types
A Pfaffian constraint is integrable iff it is holonomic. Otherwise, it is non-integrable or nonholonomic.
A Pfaffian constraint is scleronomous, or scleronomic, iff the coefficients do not depend on time. Otherwise, it is rheonomous, or rheonomic.
A Pffafian constraint is acatastatic iff . Otherwise, it is catastatic.
These together produce 8 types of Pffafian constraints, all of which are possible: {non-integrable, integrable} × {scleronomous, rheonomous} × {acatastatic, catastatic}.
A Pffafian constraint system is scleronomous/acatastic iff all its constraints are scleronomous/acatastic.
Pfaffian constraints are named after Johann Friedrich Pfaff, who studied the problem of Pfaff: Find the necessary and sufficient conditions for a Pfaffian constraint system to be integrable. In 1815, Pfaff published a general way to integrate first-order partial differential equations (PDE). The idea was to convert such a PDE in variables to a 1-form in variables, then integrate .[2][3] This problem was important in the development of modern differential geometry.[4][5] Milestones include (Clebsch, 1866),[6] (Frobenius, 1877),[7] (Darboux, 1882),[8] (Cartan, 1899).[9] See integrability conditions for differential systems for the solution.
The problem of Pfaff is nontrivial, because it is possible for two individually non-holonomic constraints to together create a holonomic constraint system. For example, on , the 1-forms and are both contact forms, thus maximally non-integrable, but a system containing both of them is integrable. Its integral manifolds are precisely the lines parallel to the z-axis.
Holonomic constraint
Given a holonomic system described by a set of holonomic constraint equations
where are the n generalized coordinates that describe the system, and where is the number of equations in a system of constraints, we can differentiate by the chain rule for each equation:
A Pfaffian constraint can be plotted as a field of surfaces of size
Nonholonomic constraint
If the constraint is nonholonomic, but first-order in the velocity, then it can also be written in Pfaffian form. That is, if in eachthe terms involving are linear in them, then it is a Pfaffian constraint. For example, is equivalent to .
Non-Pfaffian constraint
If the constraint is not first-order in velocity, then it is not a Pfaffian constraint in general. For example, the constant-speed constraint is not Pfaffian. Similarly, is not Pfaffian.
If the constraint is an inequality, then it is not Pfaffian. For example, the constraint for a pendulum with a soft string of length is .
If the constraint is not smooth, then it is not Pfaffian.
If the constraint is not restricted to position and velocity, then it is not Pfaffian in general. However, it might turn out to be equivalent to one. For example, consider a particle moving on the plane. If it is constrained to have constant curvature then , and it involves acceleration. However if we require the particle to have smooth and nonzero velocity, then it in fact moves on a circle, and thus it is a holonomic constraint.
Examples
Pendulum
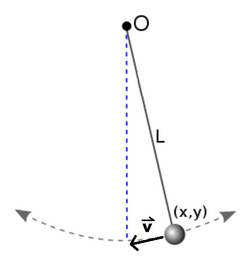
Consider a pendulum. Because of how the motion of the weight is constrained by the arm, the velocity vector of the weight must be perpendicular at all times to the position vector . Because these vectors are always orthogonal, their dot product must be zero. Both position and velocity of the mass can be defined in terms of an - coordinate system:
Simplifying the dot product yields:
We multiply both sides by . This results in the Pfaffian form of the constraint equation:
This Pfaffian form is useful, as we may integrate it to solve for the holonomic constraint equation of the system, if one exists. In this case, the integration is rather trivial:
Where C is the constant of integration.
And conventionally, we may write:
The term is squared simply because it must be a positive number; being a physical system, dimensions must all be real numbers. Indeed, is the length of the pendulum arm.
Robotics
In robot motion planning, a Pfaffian constraint is a set of k linearly independent constraints linear in velocity, i.e., of the form One source of Pfaffian constraints is rolling without slipping in wheeled robots.[10]
Rolling wheel
An upright wheel on a plane (sometimes visualized as a unicycle or a rolling upright coin) is a nonholonomic system with a single Pfaffian constraint.
Let is the steering angle relative to the -axis, and and be the location where the wheel touches the plane. Since the wheel can only move in the direction it is pointing towards, we obtain the constraint . As a 1-form, the constraint is .
References
- ↑ Ardema, Mark D. (2005). Analytical Dynamics: Theory and Applications. Kluwer Academic / Plenum Publishers. p. 57. ISBN 0-306-48681-4.
- ↑ Pfaff, Johann Friedrich (1814–1815). "Methodus generalis, aequationes differentiarum partialium nec non aequationes differentiales vulgates, ultrasque primi ordinis, inter quotcunque variables, complete integrandi" (in la). Abhandlungen der Königlichen Akademie der Wissenschaften in Berlin: 76–136. https://archive.org/details/abhandlungenderp14akad/page/76/mode/1up.
- ↑ Pfaff, Johann Friedrich (1902) (in de). Methodus generalis, aequationes differentiarum partialium nec non aequationes differentiales vulgates, ultrasque primi ordinis, inter quotcunque variables, complete integrandi. Ostwald’s Klassiker der exakten Wissenschaften. 129. Leipzig: W. Engelmann.
- ↑ Hawkins, Thomas (2005-05-01). "Frobenius, Cartan, and the Problem of Pfaff" (in en). Archive for History of Exact Sciences 59 (4): 381–436. doi:10.1007/s00407-004-0095-4. ISSN 1432-0657. https://doi.org/10.1007/s00407-004-0095-4.
- ↑ Hawkins, Thomas (2013), Hawkins, Thomas, ed., "The Problem of Pfaff" (in en), The Mathematics of Frobenius in Context: A Journey Through 18th to 20th Century Mathematics (New York, NY: Springer): pp. 155–204, doi:10.1007/978-1-4614-6333-7_6, ISBN 978-1-4614-6333-7, https://doi.org/10.1007/978-1-4614-6333-7_6
- ↑ Clebsch, Alfred (1866). "Ueber die simultane Integration linearer partieller Differentialgleichungen.". Journal für die reine und angewandte Mathematik (Crelles Journal) 1866 (65): 257–268. doi:10.1515/crll.1866.65.257. ISSN 0075-4102. https://www.degruyter.com/document/doi/10.1515/crll.1866.65.257/html.
- ↑ Frobenius, G. (1877). "Ueber das Pfaffsche Problem.". Journal für die reine und angewandte Mathematik 82: 230–315. ISSN 0075-4102. https://eudml.org/doc/148315.
- ↑ Darboux, Gaston (1882). "Sur le problème de Pfaff" (in fr). Bulletin des Sciences Mathématiques 6: 14–36, 49–68. https://gallica.bnf.fr/ark:/12148/bpt6k68005v.
- ↑ Cartan, Élie (1899). "Sur certaines expressions différentielles et le problème de Pfaff" (in fr). Annales scientifiques de l'École Normale Supérieure 16: 239–332. doi:10.24033/asens.467. ISSN 1873-2151. https://www.numdam.org/item/?h=nc&id=ASENS_1899_3_16__239_0.
- ↑ Choset, H.M. (2005). Principles of Robot Motion: Theory, Algorithms, and Implementation. The MIT Press. ISBN 0-262-03327-5.
 |
