Philosophy:The Ruliad

Short description: Concept introduced by Stephen Wolfram

A schematic figure of the Ruliad

The Ruliad is a concept introduced by Stephen Wolfram. It is defined as the entangled limit of everything that is computationally achievable: the result of following all possible computational rules in all possible ways. It can be seen as an attempt to abstract and generalize every aspect of the physical universe through the use of structures such as graphs.

The term is derived from the concept of the Rulial Space, a space defined by allowing all practicable rules of a given class to be followed between states of a system.

Basic structure

At the lowest level, the structures on which the models operate consist of collections of relations between identical discrete elements. These structures can be represented as graphs or hypergraphs, with such collections being represented as the edges, and those elements are nodes. An example of a simple rule: [math]\displaystyle{ \begin{align} \{\{x, y\}\} &\longrightarrow \{\{x, y\}\}, \\ \{\{x, y\}\} &\longrightarrow \{\{x, y\}, \{y, z\}\}, \\ \{\{0, 1\}\} &\longrightarrow \{\{0, 1\}, \{1, z\}\}. \end{align} }[/math] with [math]\displaystyle{ x }[/math], [math]\displaystyle{ y }[/math], [math]\displaystyle{ z }[/math] as three arbitrary elements; the arrow signifies a replacement or transformation between relations. Note that the element [math]\displaystyle{ z }[/math] can be anything, as long as it is distinct from 0 and 1, which have already been used. Continuing to apply this rule, obtains [math]\displaystyle{ \{\{0, 1\}, \{1, a\}, \{1, z\}, \{z, b\}\} }[/math] The values [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] are necessarily introduced because when operating on [math]\displaystyle{ \{0, 1\} }[/math] and [math]\displaystyle{ \{1, z\} }[/math], which may be obtained in the following: [math]\displaystyle{ \begin{align} \{0, 1\} &\longrightarrow \{\{0, 1\}, \{1, z\}\}, \\ \{1, z\} &\longrightarrow \{\{1, z\}, \{z, a\}\}. \end{align} }[/math] Henceforth, the second replacement requires a different element than the previous [math]\displaystyle{ z }[/math], and the same reasoning holds for [math]\displaystyle{ b }[/math].

When imagining to continue this process (iteratively or recursively), the branching in the graph's space may be noticed, expanding both in terms of the number of edges and nodes. In the example, with a preference for an organized top-to-bottom layout, it becomes apparent that the rule generates a binary tree.

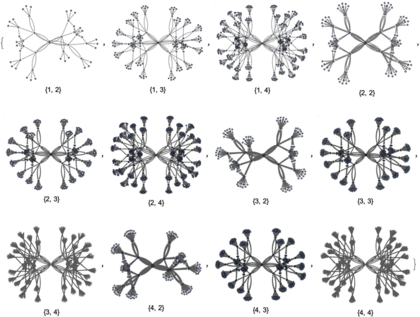
In more complex cases, the Ruliad presents correlations with the world of fractal geometry, cellular automata (like The Game Of Life by John Conway), Turing machines or growth processes of biological organisms like the Physarum Polycephalum. These are Rulial multiway graphs, after 3-steps for Turing machines (with various numbers of states):.

The full Ruliad involves taking the infinite limits of all possible rules, initial conditions and steps.

Interpretation

Hypothetically, if a rule were identified that describes (almost) everything in our Universe at the level of macro/microscopic physical laws evolving over time, reconciling both quantum mechanics and relativity (consider quantum gravity), the inevitable next question would be: "Why this rule and not others?"

The Ruliad is a mosaic of possible choices, many of which don't truly represent our surroundings. Stephen Wolfram's idea (also presented during a TED Talk) is that we are observers confined within a specific branch of the Ruliad. We cannot observe the overall picture from the outside, but we tend to analyze specific facets of the Ruliad through particular methods of empirical perception and analysis.

Moreover, what we observe in the present, what we observed in the past, and what we will observe in the near future may not necessarily coincide with what we would see with an infinitely long time available for the evolution of the Ruliad. We are not capable of predicting with a high degree of accuracy how the structure will evolve over time, especially when considering long-term "distances" and rules that can occur in any way without constraints. The evolution of such a complex system is hardly predictable, even with the probabilistic and algorithmic tools we have today: Stephen refers to it as computational irreducibility.

So, the solution would involve a concatenation of What If scenarios and observations from various perspectives, each of which interprets the Ruliad within the confines of its own branch.

Note: there could be points of contact between multiple "universes" related to different observers (not necessarily meant as a physical entity endowed with consciousness).