Physics:3D sound localization
3D sound localization refers to an acoustic technology that is used to locate the source of a sound in a three-dimensional space. The source location is usually determined by the direction of the incoming sound waves (horizontal and vertical angles) and the distance between the source and sensors. It involves the structure arrangement design of the sensors and signal processing techniques.
Most mammals (including humans) use binaural hearing to localize sound, by comparing the information received from each ear in a complex process that involves a significant amount of synthesis. It is difficult to localize using monaural hearing, especially in 3D space.
Technology
Sound localization technology is used in some audio and acoustics fields, such as hearing aids, surveillance[1] and navigation. Existing real-time passive sound localization systems are mainly based on the time-difference-of-arrival (TDOA) approach, limiting sound localization to two-dimensional space, and are not practical in noisy conditions.
Applications
Applications of sound source localization include sound source separation, sound source tracking, and speech enhancement. Sonar uses sound source localization techniques to identify the location of a target. 3D sound localization is also used for effective human-robot interaction. With the increasing demand for robotic hearing, some applications of 3D sound localization such as human-machine interface, handicapped aid, and military applications, are being explored.[2]
Cues for sound localization
Localization cues[3] are features that help localize sound. Cues for sound localization include binaural and monoaural cues.
- Monoaural cues can be obtained via spectral analysis and are generally used in vertical localization.
- Binaural cues are generated by the difference in hearing between the left and right ears. These differences include the interaural time difference (ITD) and the interaural intensity difference (IID). Binaural cues are used mostly for horizontal localization.
How does one localize sound?
The first clue our hearing uses is interaural time difference. Sound from a source directly in front of or behind us will arrive simultaneously at both ears. If the source moves to the left or right, our ears pick up the sound from the same source arriving at both ears - but with a certain delay. Another way of saying it could be, that the two ears pick up different phases of the same signal.[4]
Methods
There are many different methods of 3D sound localization. For instance:
- Different types of sensor structure, such as microphone array and binaural hearing robot head.[5]
- Different techniques for optimal results, such as neural network, maximum likelihood and Multiple signal classification (MUSIC).
- Real-time methods using an Acoustic Vector Sensor (AVS) array [6]
- Scanning techniques[7]
- Offline methods (according to timeliness)
- Microphone Array Approach
Steered Beamformer Approach
This approach utilizes eight microphones combined with a steered beamformer enhanced by the Reliability Weighted Phase Transform (RWPHAT). The final results are filtered through a particle filter that tracks sources and prevents false directions.
The motivation of using this method is that based on previous research. This method is used for multiple sound source tracking and localizing despite soundtracking and localization only apply for a single sound source.
Beamformer-based Sound Localization
To maximize the output energy of a delay-and-sum beamformer in order to find the maximum value of the output of a beamformer steered in all possible directions. Using the Reliability Weighted Phase Transform (RWPHAT) method, The output energy of M-microphone delay-and-sum beamformer is
- [math]\displaystyle{ E = K + 2\sum_{{m}_{1}=1}^{M-1} \sum_{{m}_{2}=0}^{{m}_{1}-1}{{R}^\text{RWPHAT}}_{i,j}\left({\tau}_{{m}_{1}}-{\tau}_{{m}_{2}} \right) }[/math]
Where E indicates the energy, and K is a constant, [math]\displaystyle{ {{R}^\text{RWPHAT}}_{i,j}\left({\tau}_{{m}_{1}}-{\tau}_{{m}_{2}} \right) }[/math] is the microphone pairs cross-correlation defined by Reliability Weighted Phase Transform:
- [math]\displaystyle{ {{R}^\text{RWPHAT}}_{i,j}\left(\tau \right) = \sum_{k=0}^{L-1}\frac{{\zeta }_{i}\left(k \right){X}_{i}\left(k \right){\zeta }_{j}\left(k \right){{X}_{j}}^{*}\left(k \right)}{\left|{X}_{i}\left(k \right) \right|\left|{X}_{j}\left(k \right) \right|}{e}^{j2\pi k\tau /L} }[/math]
the weighted factor [math]\displaystyle{ {{\zeta}^{n}}_{i}\left(k \right) }[/math]reflect the reliability of each frequency component, and defined as the Wiener Filter gain [math]\displaystyle{ {{\zeta}^{n}}_{i}\left(k \right) = \frac{{{\xi }^{n}}_{i}\left(k \right)}{{{\xi }^{n}}_{i}\left(k \right)+1} }[/math], where [math]\displaystyle{ {{\xi }^{n}}_{i}\left(k \right) }[/math] is an estimate of a prior SNR at [math]\displaystyle{ i^{th} }[/math] microphone, at time frame [math]\displaystyle{ n }[/math], for frequency [math]\displaystyle{ k }[/math], computed using the decision-directed approach.[8]
The [math]\displaystyle{ x_{m_n} }[/math] is the signal from [math]\displaystyle{ {m}^{th} }[/math] microphone and [math]\displaystyle{ {\tau}_{{m}_{n}} }[/math] is the delay of arrival for that microphone. The more specific procedure of this method is proposed by Valin and Michaud[9]
The advantage of this method is that it detects the direction of the sound and derives the distance of sound sources. The main drawback of the beamforming approach is the imperfect nature of sound localization accuracy and capability, versus the neural network approach, which uses moving speakers.
Collocated Microphone Array Approach
This method relates to the technique of Real-Time sound localization utilizing an Acoustic Vector Sensor (AVS) array, which measures all three components of the acoustic particle velocity, as well as the sound pressure, unlike conventional acoustic sensor arrays that only utilize the pressure information and delays in the propagating acoustic field. Exploiting this extra information, AVS arrays are able to significantly improve the accuracy of source localization.
Acoustic Vector Array
• Contains three orthogonally placed acoustic particle velocity sensors (shown as X, Y and Z array) and one omnidirectional acoustic microphone (O).
• Commonly used both in air [10] and underwater.
• Can be used in combination with the Offline Calibration Process[11] to measure and interpolate the impulse response of X, Y, Z and O arrays, to obtain their steering vector.
A sound signal is first windowed using a rectangular window, then each resulting segment signal is created as a frame. 4 parallel frames are detected from XYZO array and used for DOA estimation. The 4 frames are split into small blocks with equal size, then the Hamming window and FFT are used to convert each block from a time domain to a frequency domain. Then the output of this system is represented by a horizontal angle and a vertical angle of the sound sources which is found by the peak in the combined 3D spatial spectrum.
The advantages of this array, compared with past microphone array, are that this device has a high performance even if the aperture is small, and it can localize multiple low frequency and high frequency wide band sound sources simultaneously. Applying an O array can make more available acoustic information, such as amplitude and time difference. Most importantly, XYZO array has a better performance with a tiny size.
The AVS is one kind of collocated multiple microphone array, it makes use of a multiple microphone array approach for estimating the sound directions by multiple arrays and then finds the locations by using reflection information such as where the direction is detected where different arrays cross.
Motivation of the Advanced Microphone array
Sound reflections always occur in an actual environment and microphone arrays[12] cannot avoid observing those reflections. This multiple array approach was tested using fixed arrays in the ceiling; the performance of the moving scenario still need to be tested.
Learning how to apply Multiple Microphone Array
Angle uncertainty (AU) will occur when estimating direction, and position uncertainty (PU) will also aggravate with increasing distance between the array and the source. We know that:
- [math]\displaystyle{ PU \left(r \right)= \frac{\pm AU}{360 } \times 2 \pi \times r }[/math]
Where r is the distance between array center to source, and AU is angle uncertainly. Measurement is used for judging whether two directions cross at some location or not. Minimum distance between two lines:
- [math]\displaystyle{ dist \left(dir_1,dir_2 \right)=\frac{ \left( \overrightarrow{v_1} \times \overrightarrow{v_2} \right) \times \overrightarrow{p_1 p_2}}{ \left| \overrightarrow{v_1} \times \overrightarrow{v_2} \right|} }[/math]
where[math]\displaystyle{ dir_1 }[/math]and [math]\displaystyle{ dir_2 }[/math] are two directions, [math]\displaystyle{ v_i }[/math]are vectors parallel to detected direction, and [math]\displaystyle{ p_i }[/math]are the position of arrays.
If
- [math]\displaystyle{ dist(dir_1,dir_2)\lt abs(PU_1(r_1))+abs(PU_2(r_2)) }[/math]
Two lines are judged as crossing. When two lines are crossing, we can compute the sound source location using the following:
- [math]\displaystyle{ \mathrm{POS}_{source} = \frac {\left( \mathrm{POS}_1 \times w_1 + \mathrm{POS}_2 \times w_2 \right)}{w_1 + w_2 } }[/math]
[math]\displaystyle{ \mathrm{POS}_{source} }[/math]is the estimation of sound source position, [math]\displaystyle{ \mathrm{POS}_n }[/math] is the position where each direction intersect the line with minimum distance, and [math]\displaystyle{ w_n }[/math] is the weighted factors. As the weighting factor [math]\displaystyle{ w_n }[/math], we determined use [math]\displaystyle{ PU }[/math] or [math]\displaystyle{ r }[/math] from the array to the line with minimum distance.
Scanning Techniques
thumb|3D sound localization of a large compressor[13] Scan-based techniques are a powerful tool for localizing and visualizing time-stationary sound sources, as they only require the use of a single sensor and a position tracking system. One popular method for achieving this is through the use of an Acoustic Vector Sensor (AVS), also known as a 3D Sound Intensity Probe, in combination with a 3D tracker.
The measurement procedure involves manually moving the AVS sensor around the sound source while a stereo camera is used to extract the instantaneous position of the sensor in three-dimensional space. The recorded signals are then split into multiple segments and assigned to a set of positions using a spatial discretization algorithm. This allows for the computation of a vector representation of the acoustic variations across the sound field, using combinations of the sound pressure and the three orthogonal acoustic particle velocities.
The results of the AVS analysis can be presented over a 3D sketch of the tested object, providing a visual representation of the sound distribution around a 3D mesh of the object or environment. This can be useful for localizing sound sources in a variety of fields, such as architectural acoustics, noise control, and audio engineering, as it allows for a detailed understanding of the sound distribution and its interactions with the surrounding environment.
Learning method for binaural hearing
Binaural hearing learning[5] is a bionic method. The sensor is a robot dummy head with 2 sensor microphones along with the artificial pinna (reflector). The robot head has 2 rotation axes and can rotate horizontally and vertically. The reflector causes the spectrum change into a certain pattern for incoming white noise sound wave and this pattern is used for the cue of the vertical localization. The cue for horizontal localization is ITD. The system makes use of a learning process using neural networks by rotating the head with a settled white noise sound source and analyzing the spectrum. Experiments show that the system can identify the direction of the source well in a certain range of angle of arrival. It cannot identify the sound coming outside the range due to the collapsed spectrum pattern of the reflector. Binaural hearing use only 2 microphones and is capable of concentrating on one source among multiple sources of noises.
In the real sound localization, the robot head and the torso play a functional role, in addition to the two pinnae. This functions as spatial linear filtering and the filtering is always quantified in terms of Head-Related Transfer Function (HRTF).[14] HRTF also uses the robot head sensor, which is the binaural hearing model. The HRTF can be derived based on various cues for localization. Sound localization with HRTF is filtering the input signal with a filter which is designed based on the HRTF. Instead of using the neural networks, a head-related transfer function is used and the localization is based on a simple correlation approach.
See more: Head-related transfer function.
Cross-power spectrum phase (CSP) analysis
CSP method[15] is also used for the binaural model. The idea is that the angle of arrival can be derived through the time delay of arrival (TDOA) between two microphones, and TDOA can be estimated by finding the maximum coefficients of CSP. CSP coefficients are derived by:
- [math]\displaystyle{ csp_{ij}(k)=\text{IFFT}\left \{ \frac{\text{FFT}[s_{i}(n)]\cdot \text{FFT}[s_{j}(n)]^*} {\left |\text{FFT}[s_{i}(n)]\right \vert \cdot \left |\text{FFT}[s_{j}(n)]\right \vert \quad} \right \} \quad }[/math]
Where [math]\displaystyle{ s_{i}(n) }[/math] and [math]\displaystyle{ s_{j}(n) }[/math] are signals entering the microphone [math]\displaystyle{ i }[/math] and [math]\displaystyle{ j }[/math] respectively
Time delay of arrival([math]\displaystyle{ \tau }[/math]) then can be estimated by:
- [math]\displaystyle{ {\tau}= \operatorname{arg} \max\{csp_{ij}(k)\} }[/math]
Sound source direction is
- [math]\displaystyle{ {\theta}=\cos^{-1}\frac{v\cdot \tau}{d_{\max}\cdot F_{s}} }[/math]
Where [math]\displaystyle{ v }[/math] is the sound propagation speed, [math]\displaystyle{ F_{s} }[/math] is the sampling frequency and [math]\displaystyle{ d_{max} }[/math] is the distance with maximum time delay between 2 microphones.
CPS method does not require the system impulse response data that HRTF needs. An expectation-maximization algorithm is also used for localizing several sound sources and reduce the localization errors. The system is capable of identifying several moving sound source using only two microphones.
2D sensor line array
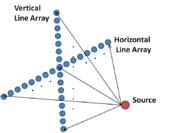
In order to estimate the location of a source in 3D space, two line sensor arrays can be placed horizontally and vertically. An example is a 2D line array used for underwater source localization.[16] By processing the data from two arrays using the maximum likelihood method, the direction, range and depth of the source can be identified simultaneously. Unlike the binaural hearing model, this method is similar to the spectral analysis method. The method can be used to localize a distant source.
Self-rotating Bi-Microphone Array
The rotation of the two-microphone array (also referred as bi-microphone array [17]) leads to a sinusoidal inter-channel time difference (ICTD) signal for a stationary sound source present in a 3D environment. The phase shift of the resulting sinusoidal signal can be directly mapped to the azimuth angle of the sound source, and the amplitude of the ICTD signal can be represented as a function of the elevation angle of the sound source and the distance between the two microphones.[18] In the case of multiple sources, the ICTD signal has data points forming multiple discontinuous sinusoidal waveforms. Machine learning techniques such as Random sample consensus (RANSAC) and Density-based spatial clustering of applications with noise (DBSCAN) can be applied to identify phase shifts (mapping to azimuths) and amplitudes (mapping to elevations) of each discontinuous sinusoidal waveform in the ICTD signal.[19]
Hierarchical Fuzzy Artificial Neural Networks Approach
The Hierarchical Fuzzy Artificial Neural Networks Approach sound localization system was modeled on biologically binaural sound localization. Some primitive animals with two ears and small brains can perceive 3D space and process sounds, although the process is not fully understood. Some animals experience difficulty in 3D sound location due to small head size. Additionally, the wavelength of communication sound may be much larger than their head diameter, as is the case with frogs.
Based on previous binaural sound localization methods, a hierarchical fuzzy artificial neural network system combines interaural time difference(ITD-based) and interaural intensity difference(IID-based) sound localization methods for higher accuracy that is similar to that of humans. Hierarchical Fuzzy Artificial Neural Networks[20] were used with the goal of the same sound localization accuracy as human ears.
IID-based or ITD-based sound localization methods have a main problem called Front-back confusion.[21] In this sound localization based on a hierarchical neural network system, to solve this issue, an IID estimation is with ITD estimation. This system was used for broadband sounds and be deployed for non-stationary scenarios.
3D sound localization for monaural sound source
Typically, sound localization is performed by using two (or more) microphones. By using the difference of arrival times of a sound at the two microphones, one can mathematically estimate the direction of the sound source. However, the accuracy with which an array of microphones can localize a sound (using Interaural time difference) is fundamentally limited by the physical size of the array. If the array is too small, then the microphones are spaced too closely together so that they all record essentially the same sound (with ITF near zero), making it extremely difficult to estimate the orientation. Thus, it is not uncommon for microphone arrays to range from tens of centimeters in length (for desktop applications) to many tens of meters in length (for underwater localization). However, microphone arrays of this size then become impractical to use on small robots. even for large robots, such microphone arrays can be cumbersome to mount and to maneuver. In contrast, the ability to localize sound using a single microphone (which can be made extremely small) holds the potential of significantly more compact, as well as lower cost and power, devices for localization.
Conventional HRTF approach
A general way to implement 3d sound localization is to use the HRTF(Head-related transfer function). First, compute HRTFs for the 3D sound localization, by formulating two equations; one represents the signal of a given sound source and the other indicates the signal output from the robot head microphones for the sound transferred from the source. Monaural input data are processed by these HRTFs, and the results are output from stereo headphones. The disadvantage of this method is that many parametric operations are necessary for the whole set of filters to realize the 3D sound localization, resulting in high computational complexity.
DSP implementation of 3D sound localization
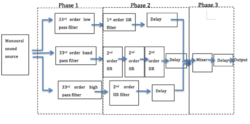
A DSP-based implementation of a realtime 3D sound localization approach with the use of an embedded DSP can reduce the computational complexity As shown in the figure, the implementation procedure of this realtime algorithm is divided into three phases, (i) Frequency Division, (ii) Sound Localization, and (iii) Mixing. In the case of 3D sound localization for a monaural sound source, the audio input data are divided into two: left and right channels and the audio input data in time series are processed one after another.[22]
A distinctive feature of this approach is that the audible frequency band is divided into three so that a distinct procedure of 3D sound localization can be exploited for each of the three subbands.
Single microphone approach
Monaural localization is made possible by the structure of the pinna (outer ear), which modifies the sound in a way that is dependent on its incident angle. A machine learning approach is adapted for monaural localization using only a single microphone and an “artificial pinna” (that distorts sound in a direction-dependent way). The approach models the typical distribution of natural and artificial sounds, as well as the direction-dependent changes to sounds induced by the pinna.[23] The experimental results also show that the algorithm is able to fairly accurately localize a wide range of sounds, such as human speech, dog barking, waterfall, thunder, and so on. In contrast to microphone arrays, this approach also offers the potential of significantly more compact, as well as lower cost and power, devices for sound localization.
See also
- 3D sound reconstruction
- Acoustic source localization
- Binaural recording
- Head-related transfer function
- Perceptual-based 3D sound localization
- Sound localization
- Vertical sound localization
References
- ↑ Keyrouz, Fakheredine; Diepold, Klaus; Keyrouz, Shady (September 2007). "High performance 3D sound localization for surveillance applications". 2007 IEEE Conference on Advanced Video and Signal Based Surveillance. pp. 563–6. doi:10.1109/AVSS.2007.4425372. ISBN 978-1-4244-1695-0. https://research.tue.nl/nl/publications/high-performance-3d-sound-localization-for-surveillance-applications(4e84634b-26f8-4424-8265-d5cd7c31a615).html.
- ↑ Kjær, Brüel. "Noise Source Identification". Brüel & Kjær. https://www.bksv.com/en/knowledge/applications/noise-source-identification.
- ↑ Goldstein, E.Bruce (2009-02-13). Sensation and Perception (Eighth ed.). Cengage Learning. pp. 293–297. ISBN 978-0-495-60149-4.
- ↑ Kjær, Brüel. "Listening in 3D". https://www.bksv.com/en/knowledge/blog/sound/sound-localization.
- ↑ 5.0 5.1 Nakashima, H.; Mukai, T. (2005). "3D Sound Source Localization System Based on Learning of Binaural Hearing". 2005 IEEE International Conference on Systems, Man and Cybernetics. 4. pp. 3534–3539. doi:10.1109/ICSMC.2005.1571695. ISBN 0-7803-9298-1.
- ↑ Liang, Yun; Cui, Zheng; Zhao, Shengkui; Rupnow, Kyle; Zhang, Yihao; Jones, Douglas L.; Chen, Deming (2012). "Real-time implementation and performance optimization of 3D sound localization on GPUs". Automation and Test in Europe Conference and Exhibition: 832–5. ISSN 1530-1591.
- ↑ Fernandez Comesana, D.; Steltenpool, S.; Korbasiewicz, M.; Tijs, E. (2015). "Direct acoustic vector field mapping: new scanning tools for measuring 3D sound intensity in 3D space". Proceedings of Euronoise: 891–895. ISSN 2226-5147. https://www.microflown.com/resources/scientific-papers/direct-acoustic-vector-field-mapping-new-scanning-tools-for-measuring-3d-sound-intensity-in-3d-space.
- ↑ Ephraim, Y.; Malah, D. (Dec 1984). "Speech enhancement using a minimum-mean square error short-time spectral amplitude estimator". IEEE Transactions on Acoustics, Speech, and Signal Processing 32 (6): 1109–21. doi:10.1109/TASSP.1984.1164453. ISSN 0096-3518.
- ↑ Valin, J.M.; Michaud, F.; Rouat, Jean (14–19 May 2006). "Robust 3D Localization and Tracking of Sound Sources Using Beamforming and Particle Filtering". 2006 IEEE International Conference on Acoustics Speech and Signal Processing Proceedings. 4. p. IV. doi:10.1109/ICASSP.2006.1661100. ISBN 978-1-4244-0469-8.
- ↑ Pérez Cabo, Daniel; de Bree, Hans Elias; Fernandez Comesaña, Daniel; Sobreira Seoane, Manuel. "Real life harmonic source localization using a network of acoustic vector sensors". EuroNoise 2015. https://www.microflown.com/resources/scientific-papers/real-life-harmonic-source-localization-using-a-network-of-acoustic-vector-sensors.
- ↑ Salas Natera, M.A.; Martinez Rodriguez-Osorio, R.; de Haro Ariet, L.; Sierra Perez, M. (2012). "Calibration Proposal for New Antenna Array Architectures and Technologies for Space Communications". IEEE Antennas and Wireless Propagation Letters 11: 1129–32. doi:10.1109/LAWP.2012.2215952. ISSN 1536-1225. Bibcode: 2012IAWPL..11.1129S. http://oa.upm.es/16395/.
- ↑ Ishi, C.T.; Even, J.; Hagita, N. (November 2013). "Using multiple microphone arrays and reflections for 3D localization of sound sources". 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems. pp. 3937–42. doi:10.1109/IROS.2013.6696919. ISBN 978-1-4673-6358-7.
- ↑ "Reducing noise emissions from Lontra's LP2 compressor". https://www.microflown.com/case-studies/reducing-noise-emissions-from-lontras-lp2-compressor.
- ↑ Keyrouz, Fakheredine; Diepold, Klaus (2006). "An Enhanced Binaural 3D Sound Localization Algorithm". 2006 IEEE International Symposium on Signal Processing and Information Technology. pp. 662–665. doi:10.1109/ISSPIT.2006.270883. ISBN 0-7803-9754-1. https://zenodo.org/record/889300.
- ↑ Hyun-Don Kim; Komatani, K.; Ogata, T.; Okuno,H.G. (Jan 2008). "Evaluation of Two-Channel-Based Sound Source Localization using 3D Moving Sound Creation Tool". ICERI 2008. doi:10.1109/ICKS.2008.25.
- ↑ Tabrikian,J.; Messer,H. (Jan 1996). "Three-Dimensional Source Localization in a Waveguide". IEEE Transactions on Signal Processing 44 (1): 1–13. doi:10.1109/78.482007. Bibcode: 1996ITSP...44....1T.
- ↑ Gala, Deepak; Lindsay, Nathan; Sun, Liang (July 2018). "Realtime Active Sound Source Localization for Unmanned Ground Robots Using a Self-Rotational Bi-Microphone Array". Journal of Intelligent & Robotic Systems 95 (3): 935–954. doi:10.1007/s10846-018-0908-3.
- ↑ Gala, Deepak; Lindsay, Nathan; Sun, Liang (June 2018). "Three-dimensional sound source localization for unmanned ground vehicles with a self-rotational two-microphone array". CDSR 2018. doi:10.11159/cdsr18.104.
- ↑ Gala, Deepak; Lindsay, Nathan; Sun, Liang (Oct 2021). "Multi-Sound-Source Localization Using Machine Learning for Small Autonomous Unmanned Vehicles with a Self-Rotating Bi-Microphone Array". 103. doi:10.1007/s10846-021-01481-4.
- ↑ Keyrouz, Fakheredine; Diepold, Klaus (May 2008). "A novel biologically inspired neural network solution for robotic 3D sound source sensing". Soft Computing 12 (7): 721–9. doi:10.1007/s00500-007-0249-9. ISSN 1432-7643.
- ↑ Hill, P.A.; Nelson, P.A.; Kirkeby, O.; Hamada, H. (December 2000). "Resolution of front-back confusion in virtual acoustic imaging systems". Journal of the Acoustical Society of America 108 (6): 2901–10. doi:10.1121/1.1323235. ISSN 0001-4966. PMID 11144583. Bibcode: 2000ASAJ..108.2901H.
- ↑ Noriaki, Sakamoto; wataru, Kobayashi; Takao, Onoye; Isao, Shirakawa (2001). "DSP implementation of 3D sound localization algorithm for monaural sound source". ICECS 2001. 8th IEEE International Conference on Electronics, Circuits and Systems (Cat. No.01EX483). 2. pp. 1061–1064. doi:10.1109/ICECS.2001.957673. ISBN 978-0-7803-7057-9.
- ↑ Saxena, A.; Ng, A.Y. (2009). "Learning sound location from a single microphone". 2009 IEEE International Conference on Robotics and Automation. pp. 1737–1742. doi:10.1109/ROBOT.2009.5152861. ISBN 978-1-4244-2788-8.
External links
 |  |
