Physics:Acoplanarity
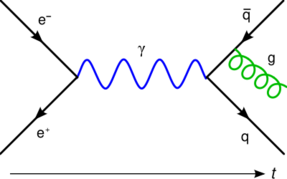
In particle physics, the acoplanarity of a scattering experiment is the degree to which the paths of the scattered particles deviate from being coplanar. Measurements of acoplanarity provide a test of perturbative quantum chromodynamics, because QCD predicts that the emission of gluons can lead to acoplanar scattering events.[1]
Measures of acoplanarity
For a two-jet final state, a useful measure of acoplanarity is
where are the azimuthal angles of the final state jets with respect to the beam line.[2] An alternative measure of acoplanarity which is infrared safe and which works for broad jets of many particles is given by
where are the momenta of the final state particles and are the components of these momenta perpendicular to a plane chosen such that A is minimized.[1] In the case of two coplanar final state particles, the plane which minimizes A would contain the paths of both particles and the beamline, and A would equal 0.
See also
References
- ↑ 1.0 1.1 De Rújula, A.; Ellis, J.; Floratos, E. G.; Gaillard, M. K. (1978). "QCD predictions for hadronic final states in e +e - annihilation". Nuclear Physics B 138 (3): 387–429. doi:10.1016/0550-3213(78)90388-7. Bibcode: 1978NuPhB.138..387D. https://cds.cern.ch/record/132816/files/197803202.pdf.
- ↑ Bordes, G.; Nicolaidis, A. (1980). "Acoplanarity distributions at large transverse momenta". Physical Review D 22 (9): 2152–2156. doi:10.1103/PhysRevD.22.2152. Bibcode: 1980PhRvD..22.2152B.
 |
