Physics:Bell's spaceship paradox

From HandWiki
Short description: Thought experiment in special relativity
Above: In S the distance between the spaceships stays the same, while the string contracts. Below: In S′ the distance between the spaceships increases, while the string length stays the same.

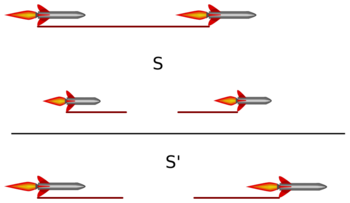
Bell's spaceship paradox is a thought experiment in special relativity. It was first described by E. Dewan and M. Beran in 1959[1] but became more widely known after John Stewart Bell elaborated the idea further in 1976.[2] A delicate thread hangs between two spaceships headed in the same direction. They start accelerating simultaneously and equally as measured in the inertial frame S, thus having the same velocity at all times as viewed from S. Therefore, they are all subject to the same Lorentz contraction, so the entire assembly seems to be equally contracted in the S frame with respect to the length at the start. At first sight, it might appear that the thread will not break during acceleration.

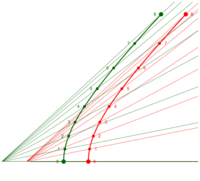
This argument, however, is incorrect as shown by Dewan and Beran, and later Bell.[1][2] The distance between the spaceships does not undergo Lorentz contraction with respect to the distance at the start, because in S, it is effectively defined to remain the same, due to the equal and simultaneous acceleration of both spaceships in S. It also turns out that the rest length between the two has increased in the frames in which they are momentarily at rest (S′), because the accelerations of the spaceships are not simultaneous here due to relativity of simultaneity. The thread, on the other hand, being a physical object held together by electrostatic forces, maintains the same rest length. Thus, in frame S, it must be Lorentz contracted, which result can also be derived when the electromagnetic fields of bodies in motion are considered. So, calculations made in both frames show that the thread will break; in S′ due to the non-simultaneous acceleration and the increasing distance between the spaceships, and in S due to length contraction of the thread.

In the following, the rest length[3] or proper length[4] of an object is its length measured in the object's rest frame. (This length corresponds to the proper distance between two events in the special case, when these events are measured simultaneously at the endpoints in the object's rest frame.[4])

Dewan and Beran

Dewan and Beran stated the thought experiment by writing:

"Consider two identically constructed rockets at rest in an inertial frame S. Let them face the same direction and be situated one behind the other. If we suppose that at a prearranged time both rockets are simultaneously (with respect to S) fired up, then their velocities with respect to S are always equal throughout the remainder of the experiment (even though they are functions of time). This means, by definition, that with respect to S the distance between the two rockets does not change even when they speed up to relativistic velocities."[1]

Then this setup is repeated again, but this time the back of the first rocket is connected with the front of the second rocket by a silk thread. They concluded:

"According to the special theory the thread must contract with respect to S because it has a velocity with respect to S. However, since the rockets maintain a constant distance apart with respect to S, the thread (which we have assumed to be taut at the start) cannot contract: therefore a stress must form until for high enough velocities the thread finally reaches its elastic limit and breaks."[1]

Dewan and Beran also discussed the result from the viewpoint of inertial frames momentarily comoving with the first rocket, by applying a Lorentz transformation:

"Since [math]\displaystyle{ \scriptstyle t'=(t-vx/c^{2})/\sqrt{1-v^{2}/c^{2}} }[/math], (..) each frame used here has a different synchronization scheme because of the [math]\displaystyle{ vx/c^{2} }[/math] factor. It can be shown that as [math]\displaystyle{ v }[/math] increases, the front rocket will not only appear to be a larger distance from the back rocket with respect to an instantaneous inertial frame, but also to have started at an earlier time."[1]

They concluded:

"One may conclude that whenever a body is constrained to move in such a way that all parts of it have the same acceleration with respect to an inertial frame (or, alternatively, in such a way that with respect to an inertial frame its dimensions are fixed, and there is no rotation), then such a body must in general experience relativistic stresses."[1]

Then they discussed the objection, that there should be no difference between a) the distance between two ends of a connected rod, and b) the distance between two unconnected objects which move with the same velocity with respect to an inertial frame. Dewan and Beran removed those objections by arguing:

  • Since the rockets are constructed exactly the same way, and starting at the same moment in S with the same acceleration, they must have the same velocity all of the time in S. Thus, they are traveling the same distances in S, so their mutual distance cannot change in this frame. Otherwise, if the distance were to contract in S, then this would imply different velocities of the rockets in this frame as well, which contradicts the initial assumption of equal construction and acceleration.
  • They also argued that there indeed is a difference between a) and b): Case a) is the ordinary case of length contraction, based on the concept of the rod's rest length l0 in S0, which always stays the same as long as the rod can be seen as rigid. Under those circumstances, the rod is contracted in S. But the distance cannot be seen as rigid in case b) because it is increasing due to unequal accelerations in S0, and the rockets would have to exchange information with each other and adjust their velocities in order to compensate for this – all of those complications don't arise in case a).

Bell

Vertical arrangement as suggested by Bell.

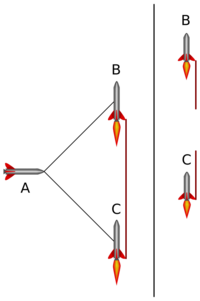
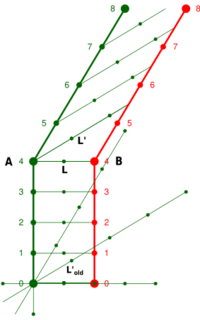
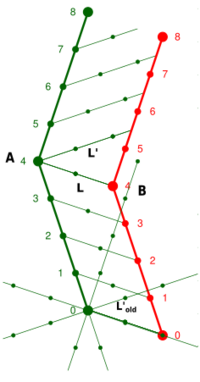
In Bell's version of the thought experiment, three spaceships A, B and C are initially at rest in a common inertial reference frame, B and C being equidistant to A. Then, a signal is sent from A to reach B and C simultaneously, causing B and C starting to accelerate in the vertical direction (having been pre-programmed with identical acceleration profiles), while A stays at rest in its original reference frame. According to Bell, this implies that B and C (as seen in A's rest frame) "will have at every moment the same velocity, and so remain displaced one from the other by a fixed distance." Now, if a fragile thread is tied between B and C, it's not long enough anymore due to length contractions, thus it will break. He concluded that "the artificial prevention of the natural contraction imposes intolerable stress".[2]

Bell reported that he encountered much skepticism from "a distinguished experimentalist" when he presented the paradox. To attempt to resolve the dispute, an informal and non-systematic survey of opinion at CERN was held. According to Bell, there was "clear consensus" which asserted, incorrectly, that the string would not break. Bell goes on to add,

"Of course, many people who get the wrong answer at first get the right answer on further reflection. Usually they feel obliged to work out how things look to observers B or C. They find that B, for example, sees C drifting further and further behind, so that a given piece of thread can no longer span the distance. It is only after working this out, and perhaps only with a residual feeling of unease, that such people finally accept a conclusion which is perfectly trivial in terms of A's account of things, including the Fitzgerald contraction."

Importance of length contraction

In general, it was concluded by Dewan & Beran and Bell, that relativistic stresses arise when all parts of an object are accelerated the same way with respect to an inertial frame, and that length contraction has real physical consequences. For instance, Bell argued that the length contraction of objects as well as the lack of length contraction between objects in frame S can be explained using relativistic electromagnetism. The distorted electromagnetic intermolecular fields cause moving objects to contract, or to become stressed if hindered from doing so. In contrast, no such forces act on the space between objects.[2] (Generally, Richard Feynman demonstrated how the Lorentz transformation can be derived from the case of the potential of a charge moving with constant velocity (as represented by the Liénard–Wiechert potential). As to the historical aspect, Feynman alluded to the circumstance that Hendrik Lorentz arrived essentially the same way at the Lorentz transformation,[5] see also History of Lorentz transformations.)

However, Petkov (2009)[6] and Franklin (2009)[3] interpret this paradox differently. They agreed with the result that the string will break due to unequal accelerations in the rocket frames, which causes the rest length between them to increase (see the Minkowski diagram in the analysis section). However, they denied the idea that those stresses are caused by length contraction in S. This is because, in their opinion, length contraction has no "physical reality", but is merely the result of a Lorentz transformation, i.e. a rotation in four-dimensional space which by itself can never cause any stress at all. Thus the occurrence of such stresses in all reference frames including S and the breaking of the string is supposed to be the effect of relativistic acceleration alone.[3][6]

Discussions and publications

Paul Nawrocki (1962) gives three arguments why the string should not break,[7] while Edmond Dewan (1963) showed in a reply that his original analysis still remains valid.[8] Many years later and after Bell's book, Matsuda and Kinoshita reported receiving much criticism after publishing an article on their independently rediscovered version of the paradox in a Japanese journal. Matsuda and Kinoshita do not cite specific papers, however, stating only that these objections were written in Japanese.[9]

However, in most publications it is agreed that the string will break, with some reformulations, modifications and different scenarios, such as by Evett & Wangsness (1960),[10] Dewan (1963),[8] Romain (1963),[11] Evett (1972),[12] Gershtein & Logunov (1998),[13] Tartaglia & Ruggiero (2003),[14] Cornwell (2005),[15] Flores (2005),[16] Semay (2006),[17] Styer (2007),[18] Freund (2008),[19] Redzic (2008),[20] Peregoudov (2009),[21] Redžić (2009),[22] Gu (2009),[23] Petkov (2009),[6] Franklin (2009),[3] Miller (2010),[24] Fernflores (2011),[25] Kassner (2012),[26] Natario (2014),[27] Lewis, Barnes & Sticka (2018),[28] Bokor (2018).[29] A similar problem was also discussed in relation to angular accelerations: Grøn (1979),[30] MacGregor (1981),[31] Grøn (1982, 2003).[32][33]

Immediate acceleration

Minkowski diagram: Length [math]\displaystyle{ L' }[/math] between the ships in S′ after acceleration is longer than the previous length [math]\displaystyle{ L'_{old} }[/math] in S′, and longer than the unchanged length [math]\displaystyle{ L }[/math] in S. The thin lines are "lines of simultaneity".
Loedel diagram of the same scenario

Similarly, in the case of Bell's spaceship paradox the relation between the initial rest length [math]\displaystyle{ L }[/math] between the ships (identical to the moving length in S after acceleration) and the new rest length [math]\displaystyle{ L' }[/math] in S′ after acceleration, is:[3][6][8][16]

[math]\displaystyle{ L'=\gamma L }[/math].

This length increase can be calculated in different ways. For instance, if the acceleration is finished the ships will constantly remain at the same location in the final rest frame S′, so it's only necessary to compute the distance between the x-coordinates transformed from S to S′. If [math]\displaystyle{ x_{A} }[/math] and [math]\displaystyle{ x_{B}=x_{A}+L }[/math] are the ships' positions in S, the positions in their new rest frame S′ are:[3]

[math]\displaystyle{ \begin{align} x'_{A}& = \gamma\left(x_{A}-vt\right)\\ x'_{B}& = \gamma\left(x_{A}+L-vt\right)\\ L'& = x'_{B}-x'_{A}\\ & =\gamma L \end{align} }[/math]

Another method was shown by Dewan (1963) who demonstrated the importance of relativity of simultaneity.[8] The perspective of frame S′ is described, in which both ships will be at rest after the acceleration is finished. The ships are accelerating simultaneously at [math]\displaystyle{ t_A = t_B }[/math] in S (assuming acceleration in infinitesimal small time), though B is accelerating and stopping in S′ before A due to relativity of simultaneity, with the time difference:

[math]\displaystyle{ \begin{align} \Delta t' & = t'_{B}-t'_{A}=\gamma\left(t_{B}-\frac{vx_{B}}{c^{2}}\right)-\gamma\left(t_{A}-\frac{vx_{A}}{c^{2}}\right)\\ & = \frac{\gamma vL}{c^{2}} \end{align} }[/math]

Since the ships are moving with the same velocity in S′ before acceleration, the initial rest length [math]\displaystyle{ L }[/math] in S is shortened in S′ by [math]\displaystyle{ L'_{old}=L/\gamma }[/math] due to length contraction. From the frame of S′, B starts accelerating before A and also stops accelerating before A. Due to this B will always have higher velocity than A up until the moment A is finished accelerating too, and both of them are at rest with respect to S′. The distance between B and A keeps on increasing till A stops accelerating. Although A's acceleration timeline is delayed by an offset of [math]\displaystyle{ \Delta t' }[/math], both A and B cover the same distance in their respective accelerations. But B's timeline contains acceleration and also being at rest in S` for [math]\displaystyle{ \Delta t' }[/math] till A stops accelerating. Hence the extra distance covered by B during the entire course can be calculated by measuring the distance traveled by B during this phase. Dewan arrived at the relation (in different notation):[8]

[math]\displaystyle{ \begin{align} L'& = L'_{old}+v\Delta t'=\frac{L}{\gamma}+\frac{\gamma v^{2}L}{c^{2}}\\ & = \gamma L \end{align} }[/math]

It was also noted by several authors that the constant length in S and the increased length in S′ is consistent with the length contraction formula [math]\displaystyle{ L=L'/\gamma }[/math], because the initial rest length [math]\displaystyle{ L }[/math] is increased by [math]\displaystyle{ \gamma }[/math] in S′, which is contracted in S by the same factor, so it stays the same in S:[6][14][18]

[math]\displaystyle{ L_{contr.}=L'/\gamma=\gamma L/\gamma=L }[/math]

Summarizing: While the rest distance between the ships increases to [math]\displaystyle{ \gamma L }[/math] in S′, the relativity principle requires that the string (whose physical constitution is unaltered) maintains its rest length [math]\displaystyle{ L }[/math] in its new rest system S′. Therefore, it breaks in S′ due to the increasing distance between the ships. As explained above, the same is also obtained by only considering the start frame S using length contraction of the string (or the contraction of its moving molecular fields) while the distance between the ships stays the same due to equal acceleration.

Constant proper acceleration

The world lines (navy blue curves) of two observers A and B who accelerate in the same direction with the same constant magnitude proper acceleration (hyperbolic motion). At A′ and B′, the observers stop accelerating.
Two observers in Born rigid acceleration, having the same Rindler horizon. They can choose the proper time of one of them as the coordinate time of the Rindler frame.
Two observers having the same proper acceleration (Bell's spaceships). They are not at rest in the same Rindler frame, and therefore have different Rindler horizons
Main pages: Physics:Hyperbolic motion (relativity), Physics:Rindler coordinates, and Physics:Born rigidity

Instead of instantaneous changes of direction, special relativity also allows to describe the more realistic scenario of constant proper acceleration, i.e. the acceleration indicated by a comoving accelerometer. This leads to hyperbolic motion, in which the observer continuously changes momentary inertial frames[34]

[math]\displaystyle{ \begin{align}x & =\frac{c^{2}}{\alpha}\left(\sqrt{1+\left(\frac{\alpha t}{c}\right)^{2}}-1\right)=\frac{c^{2}}{\alpha}\left(\cosh\frac{\alpha\tau}{c}-1\right)\\ c\tau & =\frac{c^{2}}{\alpha}\operatorname{asinh}\frac{\alpha t}{c},\quad ct=\frac{c^{2}}{\alpha}\sinh\frac{\alpha\tau}{c} \end{align} }[/math]

where [math]\displaystyle{ t }[/math] is the coordinate time in the external inertial frame, and [math]\displaystyle{ \tau }[/math] the proper time in the momentary frame, and the momentary velocity is given by

[math]\displaystyle{ v=\frac{\alpha t}{\sqrt{1+\left(\frac{\alpha t}{c}\right)^{2}}}=c\tanh\frac{\alpha\tau}{c} }[/math]

The mathematical treatment of this paradox is similar to the treatment of Born rigid motion. However, rather than ask about the separation of spaceships with the same acceleration in an inertial frame, the problem of Born rigid motion asks, "What acceleration profile is required by the second spaceship so that the distance between the spaceships remains constant in their proper frame?"[35][34][36] In order for the two spaceships, initially at rest in an inertial frame, to maintain a constant proper distance, the lead spaceship must have a lower proper acceleration.[3][36][37]

This Born rigid frame can be described by using Rindler coordinates (Kottler-Møller coordinates)[34][38]

[math]\displaystyle{ \begin{align}ct & =\left(x'+\frac{c^{2}}{\alpha}\right)\sinh\frac{\alpha t'}{c}, & y & =y',\\ x & =\left(x'+\frac{c^{2}}{\alpha}\right)\cosh\frac{\alpha t'}{c}-\frac{c^{2}}{\alpha}, & z & =z'. \end{align}\ (t'=\tau) }[/math]

The condition of Born rigidity requires that the proper acceleration of the spaceships differs by[38]

[math]\displaystyle{ \alpha_{2}=\frac{\alpha_{1}}{1+\frac{\alpha_{1}L'}{c^{2}}} }[/math]

and the length [math]\displaystyle{ L'=x_{2}^{\prime}-x_{1}^{\prime} }[/math] measured in the Rindler frame (or momentary inertial frame) by one of the observers is Lorentz contracted to [math]\displaystyle{ L=x_{2}-x_{1} }[/math] in the external inertial frame by[38]

[math]\displaystyle{ L=\frac{L'}{\cosh\frac{\alpha t'}{c}}=L'\sqrt{1-\frac{v^{2}}{c^{2}}} }[/math]

which is the same result as above. Consequently, in the case of Born rigidity, the constancy of length L' in the momentary frame implies that L in the external frame decreases constantly, the thread doesn't break. However, in the case of Bell's spaceship paradox the condition of Born rigidity is broken, because the constancy of length L in the external frame implies that L' in the momentary frame increases, the thread breaks (in addition, the expression for the distance increase between two observers having the same proper acceleration becomes also more complicated in the momentary frame[17]).

See also

References

  1. ↑ 1.0 1.1 1.2 1.3 1.4 1.5 Dewan, Edmond M.; Beran, Michael J. (March 20, 1959). "Note on stress effects due to relativistic contraction". American Journal of Physics 27 (7): 517–518. doi:10.1119/1.1996214. Bibcode: 1959AmJPh..27..517D. 
  2. ↑ 2.0 2.1 2.2 2.3 J. S. Bell: How to teach special relativity, Progress in Scientific culture 1(2) (1976), pp. 1–13. Reprinted in J. S. Bell: Speakable and unspeakable in quantum mechanics (Cambridge University Press, 1987), chapter 9, pp. 67–80.
  3. ↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 Franklin, Jerrold (2010). "Lorentz contraction, Bell's spaceships, and rigid body motion in special relativity". European Journal of Physics 31 (2): 291–298. doi:10.1088/0143-0807/31/2/006. Bibcode: 2010EJPh...31..291F. 
  4. ↑ 4.0 4.1 Moses Fayngold (2009). Special Relativity and How it Works. John Wiley & Sons. p. 407. ISBN 978-3527406074. "Note that the proper distance between two events is generally not the same as the proper length of an object whose end points happen to be respectively coincident with these events. Consider a solid rod of constant proper length l(0). If you are in the rest frame K0 of the rod, and you want to measure its length, you can do it by first marking its end-points. And it is not necessary that you mark them simultaneously in K0. You can mark one end now (at a moment t1) and the other end later (at a moment t2) in K0, and then quietly measure the distance between the marks. We can even consider such measurement as a possible operational definition of proper length. From the viewpoint of the experimental physics, the requirement that the marks be made simultaneously is redundant for a stationary object with constant shape and size, and can in this case be dropped from such definition. Since the rod is stationary in K0, the distance between the marks is the proper length of the rod regardless of the time lapse between the two markings. On the other hand, it is not the proper distance between the marking events if the marks are not made simultaneously in K0." 
  5. ↑ Feynman, R.P. (1970), "21–6. The potentials for a charge moving with constant velocity; the Lorentz formula", The Feynman Lectures on Physics, 2, Reading: Addison Wesley Longman, ISBN 978-0-201-02115-8 
  6. ↑ 6.0 6.1 6.2 6.3 6.4 Vesselin Petkov (2009): Accelerating spaceships paradox and physical meaning of length contraction, arXiv:0903.5128, published in: Veselin Petkov (2009). Relativity and the Nature of Spacetime. Springer. ISBN 978-3642019623. 
  7. ↑ Nawrocki, Paul J. (October 1962). "Stress Effects due to Relativistic Contraction". American Journal of Physics 30 (10): 771–772. doi:10.1119/1.1941785. Bibcode: 1962AmJPh..30..771N. 
  8. ↑ 8.0 8.1 8.2 8.3 8.4 Dewan, Edmond M. (May 1963). "Stress Effects due to Lorentz Contraction". American Journal of Physics 31 (5): 383–386. doi:10.1119/1.1969514. Bibcode: 1963AmJPh..31..383D.  (Note that this reference also contains the first presentation of the ladder paradox.)
  9. ↑ Matsuda, Takuya; Kinoshita, Atsuya (2004). "A Paradox of Two Space Ships in Special Relativity". AAPPS Bulletin February:  ?.  eprint version
  10. ↑ Evett, Arthur A.; Wangsness, Roald K. (1960). "Note on the Separation of Relativistically Moving Rockets". American Journal of Physics 28 (6): 566. doi:10.1119/1.1935893. Bibcode: 1960AmJPh..28..566E. 
  11. ↑ Romain, Jacques E. (1963). "A Geometrical Approach to Relativistic Paradoxes". American Journal of Physics 31 (8): 576–585. doi:10.1119/1.1969686. Bibcode: 1963AmJPh..31..576R. 
  12. ↑ Evett, Arthur A. (1972). "A Relativistic Rocket Discussion Problem". American Journal of Physics 40 (8): 1170–1171. doi:10.1119/1.1986781. Bibcode: 1972AmJPh..40.1170E. 
  13. ↑ Gershtein, S. S.; Logunov, A. A. (1998). "J. S. Bell's problem". Physics of Particles and Nuclei 29 (5): 463–468. doi:10.1134/1.953086. Bibcode: 1998PPN....29..463G. 
  14. ↑ 14.0 14.1 Tartaglia, A.; Ruggiero, M. L. (2003). "Lorentz contraction and accelerated systems". European Journal of Physics 24 (2): 215–220. doi:10.1088/0143-0807/24/2/361. Bibcode: 2003EJPh...24..215T. 
  15. ↑ Cornwell, D. T. (2005). "Forces due to contraction on a cord spanning between two spaceships". EPL 71 (5): 699–704. doi:10.1209/epl/i2005-10143-x. Bibcode: 2005EL.....71..699C. 
  16. ↑ 16.0 16.1 Flores, Francisco J. (2005). "Bell's spaceships: a useful relativistic paradox". Physics Education 40 (6): 500–503. doi:10.1088/0031-9120/40/6/F03. Bibcode: 2005PhyEd..40..500F. http://digitalcommons.calpoly.edu/phil_fac/16/. 
  17. ↑ 17.0 17.1 Semay, Claude (2006). "Observer with a constant proper acceleration". European Journal of Physics 27 (5): 1157–1167. doi:10.1088/0143-0807/27/5/015. Bibcode: 2006EJPh...27.1157S. 
  18. ↑ 18.0 18.1 Styer, Daniel F. (2007). "How do two moving clocks fall out of sync? A tale of trucks, threads, and twins". American Journal of Physics 75 (9): 805–814. doi:10.1119/1.2733691. Bibcode: 2007AmJPh..75..805S. 
  19. ↑ Jürgen Freund (2008). "The Rocket-Rope Paradox (Bell's Paradox)". Special Relativity for Beginners: A Textbook for Undergraduates. World Scientific. pp. 109–116. ISBN 978-9812771599. 
  20. ↑ Redžić, Dragan V. (2008). "Note on Dewan Beran Bell's spaceship problem". European Journal of Physics 29 (3): N11–N19. doi:10.1088/0143-0807/29/3/N02. Bibcode: 2008EJPh...29...11R. 
  21. ↑ Peregoudov, D. V. (2009). "Comment on 'Note on Dewan-Beran-Bell's spaceship problem'". European Journal of Physics 30 (1): L3–L5. doi:10.1088/0143-0807/30/1/L02. Bibcode: 2009EJPh...30L...3P. 
  22. ↑ Redžić, Dragan V. (2009). "Reply to 'Comment on "Note on Dewan-Beran-Bell's spaceship problem"'". European Journal of Physics 30 (1): L7–L9. doi:10.1088/0143-0807/30/1/L03. Bibcode: 2009EJPh...30L...7R. 
  23. ↑ Gu, Ying-Qiu (2009). "Some Paradoxes in Special Relativity and the Resolutions". Advances in Applied Clifford Algebras 21 (1): 103–119. doi:10.1007/s00006-010-0244-6. 
  24. ↑ Miller, D. J. (2010). "A constructive approach to the special theory of relativity". American Journal of Physics 78 (6): 633–638. doi:10.1119/1.3298908. Bibcode: 2010AmJPh..78..633M. 
  25. ↑ Fernflores, Francisco (2011). "Bell's Spaceships Problem and the Foundations of Special Relativity". International Studies in the Philosophy of Science 25 (4): 351–370. doi:10.1080/02698595.2011.623364. http://digitalcommons.calpoly.edu/phil_fac/30/. 
  26. ↑ Kassner, Klaus (2012). "Spatial geometry of the rotating disk and its non-rotating counterpart". American Journal of Physics 80 (9): 772–781. doi:10.1119/1.4730925. Bibcode: 2012AmJPh..80..772K. 
  27. ↑ Natario, J. (2014). "Relativistic elasticity of rigid rods and strings". General Relativity and Gravitation 46 (11): 1816. doi:10.1007/s10714-014-1816-x. 
  28. ↑ Lewis, G. F., Barnes, L. A., & Sticka, M. J. (2018). "Bell's Spaceships: The Views from Bow and Stern". Publications of the Astronomical Society of Australia 35: e001. doi:10.1017/pasa.2017.70. Bibcode: 2018PASA...35....1L. 
  29. ↑ Bokor, N. (2018). "Playing Tag Relativistically". European Journal of Physics 39 (5): 055601. doi:10.1088/1361-6404/aac80c. Bibcode: 2018EJPh...39e5601B. 
  30. ↑ Grøn, Ø. (1979). "Relativistic description of a rotating disk with angular acceleration". Foundations of Physics 9 (5–6): 353–369. doi:10.1007/BF00708527. Bibcode: 1979FoPh....9..353G. 
  31. ↑ MacGregor, M. H. (1981). "Do Dewan-Beran relativistic stresses actually exist?". Lettere al Nuovo Cimento 30 (14): 417–420. doi:10.1007/BF02817127. 
  32. ↑ Grøn, Ø. (1982). "Energy considerations in connection with a relativistic rotating ring". American Journal of Physics 50 (12): 1144–1145. doi:10.1119/1.12918. Bibcode: 1982AmJPh..50.1144G. 
  33. ↑ Øyvind Grøn (2004). "Space Geometry in a Rotating Reference Frame: A Historical Appraisal". Relativity in Rotating Frames. Springer. ISBN 978-1402018053. http://areeweb.polito.it/ricerca/relgrav/solciclos/gron_d.pdf. Retrieved 2013-04-06. 
  34. ↑ 34.0 34.1 34.2 Misner, Charles; Thorne, Kip S.; Wheeler, John Archibald (1973). Gravitation. San Francisco: W. H. Freeman. p. 165. ISBN 978-0-7167-0344-0. 
  35. ↑ "Bell's Spaceship Paradox". 2017. http://math.ucr.edu/home/baez/physics/Relativity/SR/BellSpaceships/spaceship_puzzle.html. 
  36. ↑ 36.0 36.1 Nikolić, Hrvoje (6 April 1999). "Relativistic contraction of an accelerated rod". American Journal of Physics 67 (11): 1007–1012. doi:10.1119/1.19161. Bibcode: 1999AmJPh..67.1007N. 
  37. ↑ Mathpages: Born Rigidity and Acceleration
  38. ↑ 38.0 38.1 38.2 Kirk T. McDonald (2022). "Constant Acceleration and the Equivalence Principle". http://kirkmcd.princeton.edu/examples/equivalence.pdf. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Bell%27s_spaceship_paradox&oldid=3283886"