Physics:Belleville washer

Short description: Type of spring shaped like a washer

Belleville washer

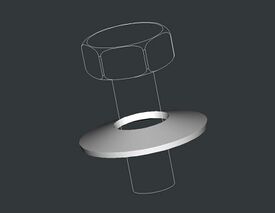
A Belleville washer, also known as a coned-disc spring, conical spring washer, disc spring, Belleville spring or cupped spring washer, is a conical shell which can be loaded along its axis either statically or dynamically. A Belleville washer is a type of spring shaped like a washer. It is the shape, a cone frustum, that gives the washer its characteristic spring.

The "Belleville" name comes from the inventor Julien Belleville who in Dunkerque, France, in 1867 patented a spring design which already contained the principle of the disc spring. The real inventor of Belleville washers is unknown.

Through the years, many profiles for disc springs have been developed. Today the most used are the profiles with or without contact flats, while some other profiles, like disc springs with trapezoidal cross-section, have lost importance.

Features and use

Cross-sectional view of an M4 anti-tank mine (circa 1945) showing the steel Belleville spring in the fuze mechanism

Cut-away view of an M14 antipersonnel landmine, showing the firing pin mounted in the centre of a plastic Belleville spring

In the different fields, if they are used as springs or to apply a flexible pre-load to a bolted joint or bearing, Belleville washers can be used as a single spring or as a stack. In a spring-stack, disc springs can be stacked in the same or in an alternating orientation and of course it is possible to stack packets of multiple springs stacked in the same direction.

Disc springs have a number of advantageous properties compared to other types of springs:

• Very large loads can be supported with a small installation space,
• Due to the nearly unlimited number of possible combinations of individual disc springs, the characteristic curve and the column length can be further varied within additional limits,
• High service life under dynamic load if the spring is properly dimensioned,
• Provided the permissible stress is not exceeded, no impermissible relaxation occurs,
• With suitable arrangement, a large damping (high hysteresis) effect may be achieved,
• Because the springs are of an annular shape, force transmission is absolutely concentric.

Thanks to these advantageous properties, Belleville washers are today used in a large number of fields, some examples are listed in the following.

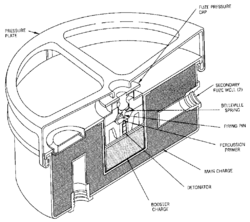
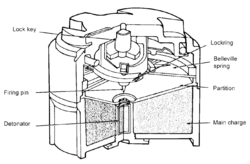
In the arms industry, Belleville springs are used, for instance, in a number of landmines e.g. the American M19, M15, M14, M1 and the Swedish Tret-Mi.59. The target (a person or vehicle) exerts pressure on the Belleville spring, causing it to exceed a trigger threshold and flip the adjacent firing pin downwards into a stab detonator, firing both it and the surrounding booster charge and main explosive filling.

Belleville washers have been used as return springs in artillery pieces, one example being the French Canet range of marine/coastal cannon from the late 1800s (75 mm, 120 mm, 152 mm).

Some makers of bolt action target rifles use Belleville washer stacks in the bolt instead of a more traditional spring to release the firing pin, as they reduce the time between trigger actuation and firing pin impact on the cartridge.

Belleville washers, without serrations which can harm the clamping surface, have no significant locking capability in bolted applications.

On aircraft (typically experimental aircraft) with wooden propellers, Belleville washers used on the mounting bolts can be useful as an indicator of swelling or shrinkage of the wood. By torquing their associated bolts to provide a specific gap between sets of washers placed with "high ends" facing each other, a change in relative moisture content in the propeller wood will result in a change of the gaps which is often great enough to be detected visually. As propeller balance depends on the weight of blades being equal, a radical difference in the washer gaps may indicate a difference in moisture content – and thus weight – in the adjacent blades.

In the aircraft and automotive industries (including Formula One cars ) disc springs are used as vibration-damping elements because of their extremely detailed tuning ability. The Cirrus SR2x series of airplanes, uses a Belleville washer setup to damp out nose gear oscillations (or "shimmy").

In the building industry, in Japan stacks of disc springs have been used under buildings as vibration dampers for earthquakes.

Belleville washers are used in some high pressure air regulators, such as those found on paintball markers and air tanks.

Stacking

Belleville spring stack in series

Belleville spring stack in parallel

Multiple Belleville washers may be stacked to modify the spring constant (or spring rate) or the amount of deflection. Stacking in the same direction will add the spring constant in parallel, creating a stiffer joint (with the same deflection). Stacking in an alternating direction is the same as adding common springs in series, resulting in a lower spring constant and greater deflection. Mixing and matching directions allow a specific spring constant and deflection capacity to be designed.

Generally, if n disc springs are stacked in parallel (facing the same direction), standing the load, the deflection of the whole stack is equal to that of one disc spring divided by n, then, to obtain the same deflection of a single disc spring the load to apply has to be n times that of a single disc spring. On the other hand, if n washers are stacked in series (facing in alternating directions), standing the load, the deflection is equal to n times that of one washer while the load to apply at the whole stack to obtain the same deflection of one disc spring has to be that of a single disc spring divided by n.

Performance considerations

In a parallel stack, hysteresis (load losses) will occur due to friction between the springs. The hysteresis losses can be advantageous in some systems because of the added damping and dissipation of vibration energy. This loss due to friction can be calculated using hysteresis methods. Ideally, no more than 4 springs should be placed in parallel. If a greater load is required, then factor of safety must be increased in order to compensate for loss of load due to friction. Friction loss is not as much of an issue in series stacks.

In a series stack, the deflection is not exactly proportional to the number of springs. This is because of a bottoming out effect when the springs are compressed to flat as the contact surface area increases once the spring is deflected beyond 95%. This decreases the moment arm and the spring will offer a greater spring resistance. Hysteresis can be used to calculate predicted deflections in a series stack. The number of springs used in a series stack is not as much of an issue as in parallel stacks even if, generally, the stack height should not be greater than three times the outside diameter of the disc spring. If it is not possible to avoid a longer stack, then it should be divided into 2 or possibly 3 partial stacks with suitable washers. These washers should be guided as exactly as possible.

As previously said, Belleville washers are useful for adjustments because different thicknesses can be swapped in and out and they can be configured to achieve essentially infinite tunability of spring rate while only filling up a small part of the technician's tool box. They are ideal in situations where a heavy spring force is required with minimal free length and compression before reaching solid height. The downside, though, is weight, and they are severely travel limited compared to a conventional coil spring when free length is not an issue.

A wave washer also acts as a spring, but wave washers of comparable size do not produce as much force as Belleville washers, nor can they be stacked in series.

Disc springs with contact flats and reduced thickness

For disc springs with a thickness of more than 6.0 mm, DIN 2093 specifies small contact surfaces at points I and III (that is the point where the load is applied and the point where the load touches the ground) in addition to the rounded corners. These contact flats improve definition of the point of load application and, particularly for spring stacks, reduce friction at the guide rod. The result is a considerable reduction in the lever arm length and a corresponding increase in the spring load. This is in turn compensated for by a reduction in the spring thickness.

The reduced thickness is specified in accordance with the following conditions:

• The overall height remains unaltered,
• The width of the contact flats (that is the annulus width) is to be approximately 1/150 of the outside diameter,
• The load applied to the reduced-thickness spring to obtain a deflection equal to the 75% of the free height (of an unreduced spring) must be the same as for an unreduced spring.

As the overall height is not reduced, springs with reduced thickness inevitably have an increased flank angle and a greater cone height than springs of the same nominal dimension without reduced thickness. Therefore, the characteristic curve is altered and becomes completely different.

Calculation

Parameterization of a Belleville disk spring

Starting from 1936, when J. O. Almen and A.Làszlò published a simplified method of calculation, always more accurate and complex methods appeared also in order to include in calculations disc springs with contact flats and reduced thickness. So, although today there are more accurate methods of calculation, the most used are the simple and convenient formulas of DIN 2092 as, for standard dimensions, they produce values which correspond well to the measured results.

Considering a Belleville washer with outside diameter [math]\displaystyle{ {D_e} }[/math], inside diameter [math]\displaystyle{ {D_i} }[/math], height [math]\displaystyle{ {l} }[/math] and thickness [math]\displaystyle{ {t} }[/math], where [math]\displaystyle{ {h_0} }[/math] is the free height, that is the difference between the height and the thickness, the following coefficients are obtained:

[math]\displaystyle{ \delta=\frac{D_e}{D_i} }[/math]

Load-deflection curves for Belleville springs, normalized by height, as described by Almen and Làszlò

[math]\displaystyle{ {C_1}=\frac{\left(\frac{t'}{t}\right)^2}{\left(\frac{1}{4}\cdot\frac{l}{t}-\frac{t'}{t}+\frac{3}{4}\right)\cdot{\left(\frac{5}{8}\cdot\frac{l}{t}-\frac{t'}{t}+\frac{3}{8}\right)} } }[/math]

[math]\displaystyle{ {C_2}=\frac{C_1}{\left(\frac{t'}{t}\right)^3}\cdot\left[\frac{5}{32}\cdot\left(\frac{l}{t}-1\right)^2+1\right] }[/math]

[math]\displaystyle{ {K_4}=\sqrt{-\frac{C_1}{2}+\sqrt{\left(\frac{C_1}{2}\right)^2+C_2}} }[/math]

The equation to calculate the load to apply to a single disc spring in order to obtain a deflection [math]\displaystyle{ {s} }[/math] is:

[math]\displaystyle{ F=\frac{4E}{1-\mu^2}\cdot\frac{t^4}{K_1-{D_e}^2}\cdot{K_4}^2\cdot\frac{s}{t}\cdot\left [{K_4}^2\cdot\left(\frac{h_0}{t}-\frac{s}{t}\right)\cdot\left(\frac{h_0}{t}-\frac{s}{2t}\right)+1\right] }[/math]

Note that for disc springs with constant thickness, [math]\displaystyle{ {t'} }[/math] is equal to [math]\displaystyle{ {t} }[/math] and consequently [math]\displaystyle{ {K_4} }[/math] is 1.

For what concerns disc springs with contact flats and reduced thickness it has to be said that a paper published in July 2013, demonstrated that the [math]\displaystyle{ {K_4} }[/math] equation as defined inside the standard norms is not correct as it would result in every reduced thickness being considered right and this is, of course, impossible. As written in that paper [math]\displaystyle{ {K_4} }[/math] should be replaced with a new coefficient, [math]\displaystyle{ {R_d} }[/math], which depends not only from the [math]\displaystyle{ \frac{t'}{t} }[/math] ratio but also from the flank angles of the spring.

The spring constant (or spring rate) is defined as:

[math]\displaystyle{ {k}=\frac{dF}{ds} }[/math]

Belleville washer stack illustration

If friction and bottoming-out effects are ignored, the spring rate of a stack of identical Belleville washers can be quickly approximated. Counting from one end of the stack, group by the number of adjacent washers in parallel. For example, in the stack of washers to the right, the grouping is 2-3-1-2, because there is a group of 2 washers in parallel, then a group of 3, then a single washer, then another group of 2.

The total spring coefficient is:

[math]\displaystyle{ K = \frac{k}{\sum_{i=1}^g \frac{1}{n_i}} }[/math]

[math]\displaystyle{ K = \frac{k}{\frac{1}{2}+\frac{1}{3}+\frac{1}{1}+\frac{1}{2}} }[/math]

[math]\displaystyle{ K = \frac{3}{7} \cdot{k} }[/math]

Where

• [math]\displaystyle{ n_i }[/math]= the number of washers in the ith group
• [math]\displaystyle{ {g} }[/math] = the number of groups
• [math]\displaystyle{ {k} }[/math] = the spring constant of one washer

So, a 2-3-1-2 stack (or, since addition is commutative, a 3-2-2-1 stack) gives a spring constant of 3/7 that of a single washer. These same 8 washers can be arranged in a 3-3-2 configuration ([math]\displaystyle{ K = \frac{6}{7}\cdot k }[/math]), a 4-4 configuration ([math]\displaystyle{ K = 2\cdot k }[/math]), a 2-2-2-2 configuration ([math]\displaystyle{ K = \frac{1}{2}\cdot k }[/math]), and various other configurations. The number of unique ways to stack [math]\displaystyle{ {n} }[/math] washers is defined by the integer partition function p(n) and increases rapidly with large [math]\displaystyle{ {n} }[/math], allowing fine-tuning of the spring constant. However, each configuration will have a different length, requiring the use of shims in most cases.

Standards

• DIN EN 16983 formerly DIN 2092 — Disc springs — Calculation
• DIN EN 16984 formerly DIN 2093 — Disc springs - Manufacturing & Quality specifications
• DIN 6796 — Conical spring washers for bolted connections