Physics:Blasius boundary layer
In physics and fluid mechanics, a Blasius boundary layer (named after Paul Richard Heinrich Blasius) describes the steady two-dimensional laminar boundary layer that forms on a semi-infinite plate which is held parallel to a constant unidirectional flow. Falkner and Skan later generalized Blasius' solution to wedge flow (Falkner–Skan boundary layer), i.e. flows in which the plate is not parallel to the flow.
Prandtl's boundary layer equations
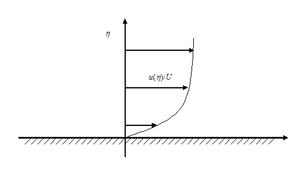
Using scaling arguments, Ludwig Prandtl[1] argued that about half of the terms in the Navier-Stokes equations are negligible in boundary layer flows (except in a small region near the leading edge of the plate). This leads to a reduced set of equations known as the boundary layer equations. For steady incompressible flow with constant viscosity and density, these read:
- Mass Continuity: [math]\displaystyle{ \dfrac{\partial u}{\partial x} + \dfrac{\partial v}{\partial y} = 0 }[/math]
- [math]\displaystyle{ x }[/math]-Momentum: [math]\displaystyle{ u \dfrac{\partial u}{\partial x} + v \dfrac{\partial u}{\partial y} = - \dfrac{1}{\rho} \dfrac{\partial p}{\partial x} + {\nu} \dfrac{\partial^2 u}{\partial y^2} }[/math]
- [math]\displaystyle{ y }[/math]-Momentum: [math]\displaystyle{ 0 = - \dfrac{\partial p}{\partial y} }[/math]
Here the coordinate system is chosen with [math]\displaystyle{ x }[/math] pointing parallel to the plate in the direction of the flow and the [math]\displaystyle{ y }[/math] coordinate pointing normal to the plate, [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math] are the [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] velocity components, [math]\displaystyle{ p }[/math] is the pressure, [math]\displaystyle{ \rho }[/math] is the density and [math]\displaystyle{ \nu }[/math] is the kinematic viscosity.
A number of similarity solutions to this set of equations have been found for various types of flow, including flow on a thin flat-plate. The term similarity refers to the property that the velocity profiles at different positions in the flow are the same apart from scaling factors. Similarity scaling factors reduce the set of partial differential equations to a relatively easily solved set of non-linear ordinary differential equations. Paul Richard Heinrich Blasius,[2] one of Prandtl's students, developed the similarity model corresponding to the flow for the case where the pressure gradient, [math]\displaystyle{ {\partial p} }[/math]/[math]\displaystyle{ {\partial x} }[/math], along a thin flat-plate is negligible compared to any pressure gradient in the boundary layer region.
Blasius equation - first-order boundary layer
Blasius showed that for the case where [math]\displaystyle{ {\partial p}/{\partial x} = 0 }[/math], the Prandtl [math]\displaystyle{ x }[/math]-momentum equation has a self-similar solution. The self-similar solution exists because the equations and the boundary conditions are invariant under the transformation
[math]\displaystyle{ x\rightarrow c^2 x, \quad y\rightarrow cy, \quad u\rightarrow u, \quad v\rightarrow \frac{v}{c} }[/math]
where [math]\displaystyle{ c }[/math] is any positive constant. He introduced the self-similar variables
[math]\displaystyle{ \eta = \dfrac{y}{\delta(x)} = y \sqrt{ \dfrac{U}{\nu x} }, \quad \psi = \sqrt{\nu U x} f(\eta) }[/math]
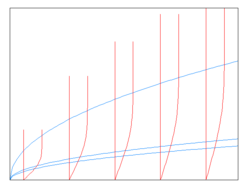
where [math]\displaystyle{ \delta(x) \propto \sqrt{ \nu x / U} }[/math] is the boundary layer thickness, [math]\displaystyle{ U }[/math] is the free stream velocity, and [math]\displaystyle{ \psi }[/math] is the stream function. The stream function is directly proportional to the normalized function, [math]\displaystyle{ f(\eta) }[/math], which is only a function of the similarity thickness variable. This leads directly to the velocity components:[3]:{{{1}}}
[math]\displaystyle{ u(x,y) = \dfrac{\partial \psi}{\partial y} = U f'(\eta), \quad v(x,y) = - \dfrac{\partial \psi}{\partial x} = \frac{1}{2}\sqrt{\dfrac{\nu U}{x}} [ \eta f'(\eta) - f(\eta)] }[/math]
Where the prime denotes derivation with respect to [math]\displaystyle{ \eta }[/math]. Substitution into the [math]\displaystyle{ x }[/math]-momentum equation gives the Blasius equation
[math]\displaystyle{ 2f^{(3)} + f'' f = 0 }[/math]
The boundary conditions are the no-slip condition, the impermeability of the wall and the free stream velocity outside the boundary layer
[math]\displaystyle{ \begin{align} u(x,0) &= 0 &\rightarrow&& f'(0) &= 0 \\ v(x,0) &= 0 &\rightarrow&& f(0) &= 0 \\ u(x,\infty) &= U &\rightarrow&& f'(\infty) &= 1 \end{align} }[/math]
This is a third-order non-linear ordinary differential equation which can be solved numerically, e.g. with the shooting method.
With the solution for [math]\displaystyle{ f }[/math] and its derivatives in hand, the Prandtl [math]\displaystyle{ y }[/math]-momentum equation can be non-dimensionalized and rearranged to obtain the [math]\displaystyle{ y }[/math]-pressure gradient, [math]\displaystyle{ {\partial p} }[/math]/[math]\displaystyle{ {\partial y} }[/math], as[4]:{{{1}}}
[math]\displaystyle{ \frac{{x^2 }}{{U^2 \delta^* }}\frac{1}{\rho }\frac{{\partial P}}{{\partial y}}\quad = \quad \frac{1}{2} \eta f^{(3)}\; + \;\frac{1}{2}f''\; - \;\frac{1}{4}ff'\; + \;\frac{1}{4}\eta f'^2 \; + \;\frac{1}{4}\eta f f'' \quad , }[/math] where [math]\displaystyle{ \delta^* }[/math] is the Blasius displacement thickness.
The Blasius normal velocity [math]\displaystyle{ v(x,y) }[/math] and the [math]\displaystyle{ y }[/math]-pressure gradient asymptotes to a value of 0.86 and 0.43, respectively, at large [math]\displaystyle{ \eta }[/math]-values whereas [math]\displaystyle{ u(x,y) }[/math] asymptotes to the free stream velocity [math]\displaystyle{ U }[/math]. As [math]\displaystyle{ \eta }[/math] goes to zero, the scaled [math]\displaystyle{ y }[/math]-pressure gradient goes to 0.16603.
The limiting form for small [math]\displaystyle{ \eta \ll 1 }[/math] is
[math]\displaystyle{ f(\eta) = \frac{1}{2}\alpha \eta^2 + O(\eta^5), \qquad \alpha = 0.332057336215196 }[/math]
and the limiting form for large [math]\displaystyle{ \eta \gg 1 }[/math] is[5]
[math]\displaystyle{ f(\eta) = \eta - \beta + O\left((\eta-\beta)^{-2} e^{-\frac{1}{2}(\eta-\beta)^2}\right), \qquad \beta =1.7207876575205 }[/math]
The characteristic parameters for boundary layers are the two sigma viscous boundary layer thickness,[6] [math]\displaystyle{ \delta_v }[/math], the displacement thickness [math]\displaystyle{ \delta^* }[/math], the momentum thickness [math]\displaystyle{ \theta }[/math], the wall shear stress [math]\displaystyle{ \tau_w }[/math] and the drag force [math]\displaystyle{ F }[/math] acting on a length [math]\displaystyle{ l }[/math] of the plate. For the Blasius solution, they are given by [math]\displaystyle{ \begin{align} \delta_{99} &\approx \delta_v = 5.29 \sqrt{\frac{\nu x}{U}} \\[1ex] \delta^* &= \delta_1 = \int_0^\infty \left(1-\frac{u}{U} \right) dy = 1.72 \sqrt{\frac{\nu x}{U}} \\[1ex] \theta &= \delta_2 = \int_0^\infty \frac{u}{U}\left(1-\frac{u}{U} \right) dy = 0.665 \sqrt{\frac{\nu x}{U}} \\[1ex] \tau_w &= \mu \left.\frac{\partial u}{\partial y}\right|_{y=0} = 0.332 \sqrt{\frac{\rho\mu U^3}{x}} \\[1ex] F &= 2 \int_0^l \tau_w dx = 1.328 \sqrt{\rho\mu l U^3} \end{align} }[/math]
The factor [math]\displaystyle{ 2 }[/math] in the drag force formula is to account both sides of the plate.
The Von Kármán Momentum integral and the energy integral for Blasius profile reduce to
[math]\displaystyle{ \begin{align} \frac{\tau_w}{\rho U^2} &= \frac{\partial \delta_2}{\partial x} + \frac{v_w}{U} \\ \frac{2\varepsilon}{\rho U^3} &= \frac{\partial \delta_3}{\partial x} + \frac{v_w}{U} \end{align} }[/math]
where [math]\displaystyle{ \tau_w }[/math] is the wall shear stress, [math]\displaystyle{ v_w }[/math] is the wall injection/suction velocity, [math]\displaystyle{ \varepsilon }[/math] is the energy dissipation rate, [math]\displaystyle{ \delta_2 }[/math] is the momentum thickness and [math]\displaystyle{ \delta_3 }[/math] is the energy thickness.
Uniqueness of Blasius solution
The Blasius solution is not unique from a mathematical perspective,[7]:{{{1}}} as Ludwig Prandtl himself noted it in his transposition theorem and analyzed by series of researchers such as Keith Stewartson, Paul A. Libby.[8] To this solution, any one of the infinite discrete set of eigenfunctions can be added, each of which satisfies the linearly perturbed equation with homogeneous conditions and exponential decay at infinity. The first of these eigenfunctions turns out to be the [math]\displaystyle{ x }[/math] derivative of the first order Blasius solution, which represents the uncertainty in the effective location of the origin.
Second-order boundary layer
This boundary layer approximation predicts a non-zero vertical velocity far away from the wall, which needs to be accounted in next order outer inviscid layer and the corresponding inner boundary layer solution, which in turn will predict a new vertical velocity and so on. The vertical velocity at infinity for the first order boundary layer problem from the Blasius equation is
[math]\displaystyle{ v = 0.86 \sqrt{\frac{\nu U}{x}} }[/math]
The solution for second order boundary layer is zero. The solution for outer inviscid and inner boundary layer are[7]:{{{1}}}
[math]\displaystyle{ \psi(x,y) \sim \begin{cases} y - \sqrt{\frac{\nu}{Ux}} \beta \ \Re \sqrt{2(x+iy)},& \text{outer } \\ \sqrt{2\nu Ux} f(\eta) + 0, & \text{inner} \end{cases} }[/math]
Again as in the first order boundary problem, any one of the infinite set of eigensolution can be added to this solution. In all the solutions [math]\displaystyle{ Re = Ux/\nu }[/math] can be considered as a Reynolds number.
Third-order boundary layer
Since the second order inner problem is zero, the corresponding corrections to third order problem is null i.e., the third order outer problem is same as second order outer problem.[7]:{{{1}}} The solution for third-order correction does not have an exact expression, but the inner boundary layer expansion is of the form,
[math]\displaystyle{ \psi(x,y) \sim \sqrt{2\nu Ux} f(\eta) + 0 + \left(\frac{\nu}{Ux}\right)^{3/2} \left[\log \left(\frac{Ux}{\nu}\right) \sqrt{\frac{x}{2}} f_{32}(\eta) + \frac{1}{\sqrt{2x}} f_{31}(\eta) \right] + \cdot\cdot\cdot }[/math]
where [math]\displaystyle{ f_{32} }[/math] is the first eigensolution of the first order boundary layer solution (which is [math]\displaystyle{ x }[/math] derivative of the first order Blasius solution) and solution for [math]\displaystyle{ f_{31} }[/math] is nonunique and the problem is left with an undetermined constant.
Blasius boundary layer with suction
Suction is one of the common methods to postpone the boundary layer separation.[9] Consider a uniform suction velocity at the wall [math]\displaystyle{ v(0)=-V }[/math]. Bryan Thwaites[10] showed that the solution for this problem is same as the Blasius solution without suction for distances very close to the leading edge. Introducing the transformation
[math]\displaystyle{ \psi = \sqrt{2 U \nu x} f(\xi,\eta), \quad \xi = V\sqrt{\frac{x}{2U\nu}}, \quad \eta = \sqrt{\frac{U}{2\nu x}}y }[/math]
into the boundary layer equations leads to
[math]\displaystyle{ u = U \frac{\partial f}{\partial \eta}, \quad v = - \sqrt{\frac{U\nu}{2x}} \left(f + \xi \frac{\partial f}{\partial \xi} - \eta \frac{\partial f}{\partial \eta} \right), }[/math] [math]\displaystyle{ \frac{\partial^3 f}{\partial \eta^3} + f \frac{\partial^2 f}{\partial \eta^2} + \xi \left(\frac{\partial f}{\partial \xi} \frac{\partial^2 f}{\partial \eta^2} - \frac{\partial^2 f}{\partial \xi\partial \eta} \frac{\partial f}{\partial \eta} \right) =0 }[/math]
with boundary conditions,
[math]\displaystyle{ f(\xi,0) =\xi, \quad \frac{\partial f}{\partial \eta}(\xi,0) =0, \quad \frac{\partial f}{\partial \eta}(\xi,\infty)=0. }[/math]
Von Mises transformation
Iglisch obtained the complete numerical solution in 1944.[11] If further von Mises transformation[12] is introduced
[math]\displaystyle{ \sigma = 2\xi, \quad \psi-Vx = \frac{U\nu}{2V} \sigma \tau^2, \quad \phi = \frac{4u^2}{U^2}, \quad \chi = U^2-u^2 = U^2\left(1-\frac{V}{4} \right), }[/math]
then the equations become
[math]\displaystyle{ \sqrt{\phi} \frac{\partial ^2 \phi}{\partial \tau^2} + \left(2\sigma\tau +\tau^3 - \frac{\sqrt{\phi}}{\tau} \right) \frac{\partial \phi}{\partial \tau} = 2\sigma \tau^2 \frac{\partial \phi}{\partial \sigma} }[/math]
with boundary conditions,
[math]\displaystyle{ \phi(0,\tau)=4, \quad \phi(\sigma,0)=0, \quad \phi(\sigma,\infty)=4. }[/math]
This parabolic partial differential equation can be marched starting from [math]\displaystyle{ \sigma=0 }[/math] numerically.
Asymptotic suction profile
Since the convection due to suction and the diffusion due to the solid wall are acting in the opposite direction, the profile will reach steady solution at large distance, unlike the Blasius profile where boundary layer grows indefinitely. The solution was first obtained by Griffith and F.W. Meredith.[13] For distances from the leading edge of the plate [math]\displaystyle{ x\gg \nu U/V^2 }[/math], both the boundary layer thickness and the solution are independent of [math]\displaystyle{ x }[/math] given by
[math]\displaystyle{ \delta = \frac{\nu}{V}, \quad u = U(1-e^{-yV/\nu}), \quad v = -V. }[/math]
Stewartson[14] studied matching of full solution to the asymptotic suction profile.
Compressible Blasius boundary layer
Here Blasius boundary layer with a specified specific enthalpy [math]\displaystyle{ h }[/math] at the wall is studied. The density [math]\displaystyle{ \rho }[/math], viscosity [math]\displaystyle{ \mu }[/math] and thermal conductivity [math]\displaystyle{ \kappa }[/math] are no longer constant here. The equation for conservation of mass, momentum and energy become
[math]\displaystyle{ \begin{align} \frac{\partial (\rho u)}{\partial x} + \frac{\partial (\rho v)}{\partial y} & = 0,\\ \rho \left(u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} \right) & = \frac{\partial }{\partial y} \left(\mu\frac{\partial u}{\partial y}\right),\\ \rho \left(u \frac{\partial h}{\partial x} + v \frac{\partial h}{\partial y} \right) &= \frac{\partial }{\partial y} \left(\frac{\mu}{Pr} \frac{\partial h}{\partial y} \right) + \mu \left( \frac{\partial u}{\partial y}\right)^2 \end{align} }[/math]
where [math]\displaystyle{ Pr=c_{p_\infty}\mu_\infty/\kappa_\infty }[/math] is the Prandtl number with suffix [math]\displaystyle{ \infty }[/math] representing properties evaluated at infinity. The boundary conditions become
[math]\displaystyle{ u = v = h - h_w(x) = 0 \ \text{for} \ y=0, }[/math] [math]\displaystyle{ u -U = h - h_\infty =0 \ \text{for} \ y=\infty \ \text{or} \ x=0. }[/math]
Unlike the incompressible boundary layer, similarity solution exists only if the transformation
[math]\displaystyle{ x\rightarrow c^2 x, \quad y\rightarrow cy, \quad u\rightarrow u, \quad v\rightarrow \frac{v}{c}, \quad h\rightarrow h, \quad \rho\rightarrow \rho, \quad \mu\rightarrow \mu }[/math]
holds and this is possible only if [math]\displaystyle{ h_w=\text{constant} }[/math].
Howarth transformation
Introducing the self-similar variables using Howarth–Dorodnitsyn transformation
[math]\displaystyle{ \eta = \sqrt{\frac{U}{2\nu_\infty x}} \int_0^y \frac{\rho}{\rho_\infty} dy, \quad f(\eta) = \frac{\psi}{\sqrt{2 \nu_\infty U x}}, \quad \tilde h(\eta) = \frac{h}{h_\infty}, \quad \tilde h_w = \frac{h_w}{h_\infty}, \quad \tilde \rho = \frac{\rho}{\rho_\infty}, \quad \tilde \mu = \frac{\mu}{\mu_\infty} }[/math]
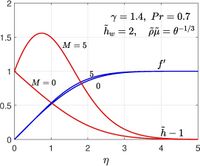
the equations reduce to [math]\displaystyle{ \begin{align} 2(\tilde\rho\tilde\mu f'')' + f f'' =0, \\ (\tilde\rho\tilde\mu \tilde h')' + Prf\tilde h' + Pr(\gamma-1)M^2 \tilde\rho\tilde\mu f''^2 =0 \end{align} }[/math] where [math]\displaystyle{ \gamma }[/math] is the specific heat ratio and [math]\displaystyle{ M=U/c_\infty }[/math] is the Mach number, where [math]\displaystyle{ c_\infty }[/math] is the speed of sound. The equation can be solved once [math]\displaystyle{ \tilde \rho = \tilde \rho(\tilde h),\ \tilde \mu = \tilde \mu(\tilde h) }[/math] are specified. The boundary conditions are
[math]\displaystyle{ f(0)=f'(0)=\theta(0)-\tilde h_w=f'(\infty)-1=\tilde h(\infty)-1=0. }[/math]
The commonly used expressions for air are [math]\displaystyle{ \gamma = 1.4, \ Pr = 0.7, \ \tilde\rho = \tilde h^{-1}, \ \tilde\mu = \tilde h^{2/3} }[/math]. If [math]\displaystyle{ c_p }[/math] is constant, then [math]\displaystyle{ \tilde h=\tilde \theta = T/T_\infty }[/math]. The temperature inside the boundary layer will increase even though the plate temperature is maintained at the same temperature as ambient, due to dissipative heating and of course, these dissipation effects are only pronounced when the Mach number [math]\displaystyle{ M }[/math] is large.
First-order Blasius boundary layer in parabolic coordinates
Since the boundary layer equations are Parabolic partial differential equation, the natural coordinates for the problem is parabolic coordinates.[7]:{{{1}}} The transformation from Cartesian coordinates [math]\displaystyle{ (x,y) }[/math] to parabolic coordinates [math]\displaystyle{ (\xi,\eta) }[/math] is given by
[math]\displaystyle{ x + i y = \tfrac{1}{2} (\xi + i \eta)^2, \quad x = \tfrac{1}{2} (\xi^2-\eta^2), \quad y = \xi \eta. }[/math]
See also
External links
- [1] - English translation of Blasius' original paper - NACA Technical Memorandum 1256.
Footnotes
- ↑ Prandtl, L. (1904). "Über Flüssigkeitsbewegung bei sehr kleiner Reibung". Verhandlinger 3. Int. Math. Kongr. Heidelberg: 484–491.
- ↑ Blasius, H. (1908). "Grenzschichten in Flüssigkeiten mit kleiner Reibung". Z. Angew. Math. Phys. 56: 1–37.
- ↑ Schlichting, H., (1979). Boundary-Layer Theory, 7th ed., McGraw-Hill, New York.
- ↑ Weyburne, David (2022). Aspects of Boundary Layer Theory. ISBN 978-0-578-98334-9.
- ↑ Boyd, J. (2008). "The Blasius function: computations before computers, the value of tricks, undergraduate projects, and open research problems". SIAM Rev. 50 (4): 791–804. doi:10.1137/070681594. Bibcode: 2008SIAMR..50..791B.
- ↑ Weyburne, D. (2014). "New thickness and shape parameters for the boundary layer velocity profile". Experimental Thermal and Fluid Science 54: 22–28. doi:10.1016/j.expthermflusci.2014.01.008.
- ↑ 7.0 7.1 7.2 7.3 Perturbation methods in fluid mechanics. Parabolic Press. 1975. ISBN 9780915760015.
- ↑ Libby, Paul A., and Herbert Fox. "Some perturbation solutions in laminar boundary-layer theory." Journal of Fluid Mechanics 17.3 (1963): 433-449.
- ↑ Rosenhead, Louis, ed. Laminar boundary layers. Clarendon Press, 1963.
- ↑ Thwaites, Bryan. On certain types of boundary-layer flow with continuous surface suction. HM Stationery Office, 1946.
- ↑ Iglisch, Rudolf. Exakte Berechnung der laminaren Grenzschicht an der längsangeströmten ebenen Platte mit homogener Absaugung. Oldenbourg, 1944.
- ↑ Von Mises, Richard. "Bemerkungen zur hydrodynamik." Z. Angew. Math. Mech 7 (1927): 425-429.
- ↑ Griffith, A. A., and F. W. Meredith. "The possible improvement in aircraft performance due to the use of boundary layer suction." Royal Aircraft Establishment Report No. E 3501 (1936): 12.
- ↑ Stewartson, K. "On asymptotic expansions in the theory of boundary layers." Studies in Applied Mathematics 36.1-4 (1957): 173-191.
References
- Parlange, J. Y.; Braddock, R. D.; Sander, G. (1981). "Analytical approximations to the solution of the Blasius equation". Acta Mech. 38 (1–2): 119–125. doi:10.1007/BF01351467. Bibcode: 1981AcMec..38..119P.
- Pozrikidis, C. (1998). Introduction to Theoretical and Computational Fluid Dynamics. Oxford. ISBN 978-0-19-509320-9.
- Schlichting, H. (2004). Boundary-Layer Theory. Springer. ISBN 978-3-540-66270-9.
- Wilcox, David C. Basic Fluid Mechanics DCW Industries Inc. 2007
- Boyd, John P. (1999), "The Blasius function in the complex plane", Experimental Mathematics 8 (4): 381–394, doi:10.1080/10586458.1999.10504626, ISSN 1058-6458, http://projecteuclid.org/getRecord?id=euclid.em/1047262359
 |  |
