Physics:Burgers material
A Burgers material is a viscoelastic material having the properties both of elasticity and viscosity. It is named after the Dutch physicist Johannes Martinus Burgers.
Overview
Maxwell representation
Given that one Maxwell material has an elasticity [math]\displaystyle{ E_1 }[/math] and viscosity [math]\displaystyle{ \eta_1 }[/math], and the other Maxwell material has an elasticity [math]\displaystyle{ E_2 }[/math] and viscosity [math]\displaystyle{ \eta_2 }[/math], the Burgers model has the constitutive equation
- [math]\displaystyle{ \sigma + \left( \frac {\eta_1} {E_1} + \frac {\eta_2} {E_2} \right) \dot\sigma + \frac {\eta_1 \eta_2} {E_1 E_2} \ddot\sigma = \left( \eta_1 + \eta_2 \right) \dot\varepsilon + \frac {\eta_1 \eta_2 \left( E_1 + E_2 \right)} {E_1 E_2} \ddot\varepsilon }[/math]
where [math]\displaystyle{ \sigma }[/math] is the stress and [math]\displaystyle{ \varepsilon }[/math] is the strain.
Kelvin representation
Given that the Kelvin material has an elasticity [math]\displaystyle{ E_1 }[/math] and viscosity [math]\displaystyle{ \eta_1 }[/math], the spring has an elasticity [math]\displaystyle{ E_2 }[/math] and the dashpot has a viscosity [math]\displaystyle{ \eta_2 }[/math], the Burgers model has the constitutive equation
- [math]\displaystyle{ \sigma + \left( \frac {\eta_1} {E_1} + \frac {\eta_2} {E_1} + \frac {\eta_2} {E_2} \right) \dot\sigma + \frac {\eta_1 \eta_2} {E_1 E_2} \ddot\sigma = \eta_2\dot\varepsilon + \frac {\eta_1 \eta_2} {E_1} \ddot\varepsilon }[/math]
where [math]\displaystyle{ \sigma }[/math] is the stress and [math]\displaystyle{ \varepsilon }[/math] is the strain.[1]
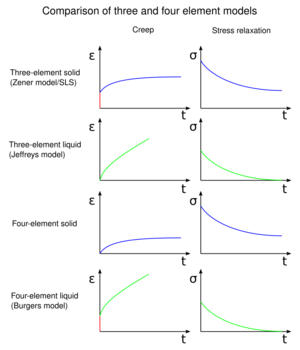
Model characteristics
This model incorporates viscous flow into the standard linear solid model, giving a linearly increasing asymptote for strain under fixed loading conditions.
See also
References
- ↑ Malkin, Alexander Ya.; Isayev, Avraam I. (2006). Rheology: Concepts, Methods, and Applications. ChemTec Publishing. pp. 59–60. ISBN 9781895198331.
External links
- Creep and Stress Relaxation for Four-Element Viscoelastic Solids and Liquids, Wolfram Demonstrations Project
 |