Physics:Disk laser

Fig.1. An optically-pumped disk laser (active mirror).

A disk laser or active mirror (Fig.1) is a type of diode pumped solid-state laser characterized by a heat sink and laser output that are realized on opposite sides of a thin layer of active gain medium. Despite their name, disk lasers do not have to be circular; other shapes have also been tried. The thickness of the disk is considerably smaller than the laser beam diameter. Initially, this laser cavity configuration had been proposed and realized experimentally for thin slice semiconductor lasers.

The disk laser concepts allow very high average and peak powers due to its large area, leading to moderate power densities on the active material.

Active mirrors and disk lasers

Fig.2. A disk laser (active mirror) configuration presented in 1992 at the SPIE conference.

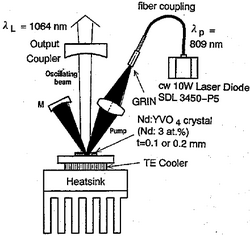
Initially, disk lasers were called active mirrors, because the gain medium of a disk laser is essentially an optical mirror with reflection coefficient greater than unity. An active mirror is a thin disk-shaped double-pass optical amplifier.

The first active mirrors were developed in the Laboratory for Laser Energetics (United States). Scalable diode-end-pumped disk Nd:YAG laser had been proposed in in Talbot active mirror configuration.

Then, the concept was developed in various research groups, in particular, the University of Stuttgart (Germany) for Yb:doped glasses.

In the disk laser, the heat sink does not have to be transparent, so, it can be extremely efficient even with large transverse size [math]\displaystyle{ ~L~ }[/math] of the device (Fig.1). The increase in size allows the power scaling to many kilowatts without significant modification of the design.

Limit of power scaling for disk lasers

Fig.3. Bouncing ray of ASE in a disk laser

The power of such lasers is limited not only by the power of pump available, but also by overheating, amplified spontaneous emission (ASE) and the background round-trip loss. To avoid overheating, the size [math]\displaystyle{ ~L~ }[/math] should be increased with power scaling. Then, to avoid strong losses due to the exponential growth of the ASE, the transverse-trip gain [math]\displaystyle{ ~u=GL~ }[/math] cannot be large. This requires reduction of the gain [math]\displaystyle{ G~ }[/math]; this gain is determined by the reflectivity of the output coupler and thickness [math]\displaystyle{ ~h }[/math]. The round-trip gain [math]\displaystyle{ ~g=2Gh~ }[/math] should remain larger than the round-trip loss [math]\displaystyle{ \beta~ }[/math] (the difference [math]\displaystyle{ g\!-\!\beta~ }[/math] determines the optical energy, which is output from the laser cavity at each round-trip). The reduction of gain [math]\displaystyle{ G~ }[/math], in a given round-trip loss [math]\displaystyle{ ~\beta~ }[/math], requires increasing the thickness [math]\displaystyle{ h }[/math]. Then, at some critical size, the disk becomes too thick and cannot be pumped above the threshold without overheating.

Some features of the power scaling can reveal from a simple model. Let [math]\displaystyle{ Q~ }[/math] be the saturation intensity, of the medium, [math]\displaystyle{ \eta_0=\omega_{\rm s}/\omega_{\rm p}~~ }[/math] be the ratio of frequencies, [math]\displaystyle{ R~ }[/math] be the thermal loading parameter. The key parameter [math]\displaystyle{ P_{\rm k}=\eta_0\frac{R^2}{Q\beta^3}~ }[/math] determines the maximal power of the disk laser. The corresponding optimal thickness can be estimated with [math]\displaystyle{ h \sim \frac{R}{Q \beta} }[/math]. The corresponding optimal size [math]\displaystyle{ L \sim \frac{R}{Q \beta^2} }[/math]. Roughly, the round-trip loss should scale inversely proportionally to the cubic root of the power required.

An additional issue is the efficient delivery of pump energy. In low round-trip gain, the single-pass absorption of the pump is also low. Therefore, recycling of pump energy is required for efficient operation. (See the additional mirror M at the left-hand side of figure 2.) For power scaling, the medium should be optically thin, with many passes of pump energy required; the lateral delivery of pump energy also might be a possible solution.

Scaling of disk lasers via self-imaging

Thin disk diode-pumped solid-state lasers may be scaled by means of transverse mode-locking in Talbot cavities. The remarkable feature of Talbot scaling is that Fresnel number [math]\displaystyle{ F }[/math] of the [math]\displaystyle{ N- }[/math] element laser array phase-locked by self-imaging is given by:

[math]\displaystyle{ F=(N-1)^2. }[/math]

The limitation on a number of phase-locked emitters [math]\displaystyle{ N }[/math] is due to randomly distributed phase distortions across an active mirror of the order [math]\displaystyle{ \lambda/10 \div \lambda/100 }[/math].

Anti-ASE cap

Fig. 4. Uncovered disk laser and that with undoped cap.

In order to reduce the impact of ASE, an anti-ASE cap consisting of undoped material on the surface of a disk laser has been suggested. Such a cap allows spontaneously emitted photons to escape from the active layer and prevents them from resonating in the cavity. Rays cannot bounce (Figure 3) as in an uncovered disk. This could allow an order of magnitude increase in the maximum power achievable by a disk laser. In both cases, the back reflection of the ASE from the edges of the disk should be suppressed. This can be done with absorbing layers, shown with green in Figure 4. At operation close to the maximal power, a significant part of the energy goes into ASE; therefore, the absorbing layers also should be supplied with heat sinks, which are not shown in the figure.

Fig. 5. Upper bound of loss [math]\displaystyle{ \beta }[/math] at which the output power [math]\displaystyle{ P_{\rm s} }[/math] of a single disk laser is still achievable. Dashed line corresponds to uncovered disk; thick solid curve represents the case with undoped cap.

Key parameter for laser materials

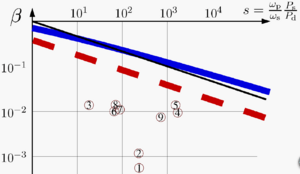
The estimate of maximal power achievable at given loss [math]\displaystyle{ \beta }[/math], is very sensitive to [math]\displaystyle{ \beta }[/math]. The estimate of the upper bound of [math]\displaystyle{ \beta }[/math], at which the desired output power [math]\displaystyle{ P_{\rm s} }[/math] is achievable is robust. This estimate is plotted versus normalized power [math]\displaystyle{ s=P_{\rm s}/P_{\rm d} }[/math] in figure 5. Here, [math]\displaystyle{ P_{\rm s} }[/math] is the output power of the laser, and [math]\displaystyle{ P_{\rm d}=R^2/Q }[/math] is the dimensional scale of power; it is related with the key parameter [math]\displaystyle{ P_{\rm k}=P_{\rm d}/\beta^3 }[/math]. The thick dashed line represents the estimate for the uncovered disk. The thick solid line shows the same for the disk with undoped cap. The thin solid line represents the qualitative estimate [math]\displaystyle{ \beta=s^{1/3} }[/math] without coefficients. Circles correspond to the experimental data for the power achieved and corresponding estimates for the background loss [math]\displaystyle{ \beta }[/math]. All future experiments and numerical simulations and estimates are expected to give values of [math]\displaystyle{ (\beta, s) }[/math], that are below the red dashed line in Fig.5 for the uncovered disks, and below the blue curve for the disks with anti-ASE cap. This can be interpreted as a scaling law for disk lasers .

In the vicinity of the curves mentioned, the efficiency of the disk laser is low; most of the pumping power goes to ASE, and is absorbed at the edges of the device. In these cases, the distribution of the pump energy available among several disks may significantly improve the performance of the lasers. Indeed, some lasers reported using several elements combined in the same cavity.

Pulsed operation

Similar scaling laws take place for pulsed operation. In quasi continuous wave regime, the maximal mean power can be estimated by scaling the saturation intensity with the fill factor of the pump, and the product of the duration of pump to the repetition rate. At short duration pulses, more detailed analysis is required . At moderate values of the repetition rate (say, higher than 1 Hz), the maximal energy of the output pulses is roughly inversely proportional to the cube of the background loss [math]\displaystyle{ \beta }[/math]; the undoped cap may provide an additional order of magnitude of mean output power, under the condition that this cap does not contribute to the background loss. At low repetition rate (and in the regime of single pulses) and sufficient pump power, there is no general limit of energy, but the required size of the device grows quickly with increase of the required pulse energy, setting the practical limit of energy; it is estimated that from a few joules to a few thousand joules can be extracted in an optical pulse from a single active element, dependently on the level of the background internal loss of the signal in the disk.

See also

• VCSEL
• VECSEL
• Thermal shock
• Round-trip gain
• Power scaling
• Gain medium
• List of laser articles