Physics:Fano resonance
In physics, a Fano resonance is a type of resonant scattering phenomenon that gives rise to an asymmetric line-shape. Interference between a background and a resonant scattering process produces the asymmetric line-shape. It is named after Italian-American physicist Ugo Fano, who in 1961 gave a theoretical explanation for the scattering line-shape of inelastic scattering of electrons from helium;[1][2] however, Ettore Majorana was the first to discover this phenomenon.[3] Fano resonance is a weak coupling effect meaning that the decay rate is so high, that no hybridization occurs.[4] The coupling modifies the resonance properties such as spectral position and width and its line-shape takes on the distinctive asymmetric Fano profile. Because it is a general wave phenomenon, examples can be found across many areas of physics and engineering.
History
The explanation of the Fano line-shape first appeared in the context of inelastic electron scattering by helium and autoionization. The incident electron doubly excites the atom to the [math]\displaystyle{ 2s2p }[/math] state, a sort of shape resonance. The doubly excited atom spontaneously decays by ejecting one of the excited electrons. Fano showed that interference between the amplitude to simply scatter the incident electron and the amplitude to scatter via autoionization creates an asymmetric scattering line-shape around the autoionization energy with a line-width very close to the inverse of the autoionization lifetime.
Explanation
The Fano resonance line-shape is due to interference between two scattering amplitudes, one due to scattering within a continuum of states (the background process) and the second due to an excitation of a discrete state (the resonant process). The energy of the resonant state must lie in the energy range of the continuum (background) states for the effect to occur. Near the resonant energy, the background scattering amplitude typically varies slowly with energy while the resonant scattering amplitude changes both in magnitude and phase quickly. It is this variation that creates the asymmetric profile.
For energies far from the resonant energy [math]\displaystyle{ E_\mathrm{res} }[/math] the background scattering process dominates. Within [math]\displaystyle{ 2\Gamma_\mathrm{res} }[/math] of the resonant energy, the phase of the resonant scattering amplitude changes by [math]\displaystyle{ \pi }[/math]. It is this rapid variation in phase that creates the asymmetric line-shape.
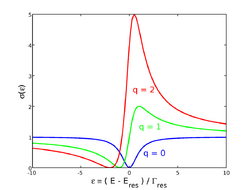
Fano showed that the total scattering cross-section [math]\displaystyle{ \sigma }[/math] assumes the following form,
[math]\displaystyle{ \sigma \approx \frac{\left(q\Gamma_\mathrm{res}/2 + E - E_\mathrm{res}\right)^2}{\left(\Gamma_\mathrm{res}/2\right)^2 + \left(E-E_\mathrm{res}\right)^2} }[/math]
where [math]\displaystyle{ \Gamma_\mathrm{res} }[/math] describes the line width of the resonant energy and q, the Fano parameter, measures the ratio of resonant scattering to the direct (background) scattering amplitude. This is consistent with the interpretation within the Feshbach–Fano partitioning theory. In the case the direct scattering amplitude vanishes, the q parameter becomes zero and the Fano formula becomes :
[math]\displaystyle{ \sigma(q=0) \approx \frac{\left(E - E_\mathrm{res}\right)^2}{\left(\Gamma_\mathrm{res}/2\right)^2 + \left(E-E_\mathrm{res}\right)^2} }[/math]
Looking at transmission shows that this last expression boils down to the expected Breit–Wigner (Lorentzian) formula, as [math]\displaystyle{ 1 - \sigma(q=0) \approx \frac{\left(\Gamma_\mathrm{res}/2\right)^2}{\left(\Gamma_\mathrm{res}/2\right)^2 + \left(E-E_\mathrm{res}\right)^2} = f(E;E_\mathrm{res},\Gamma_\mathrm{res}/2,1) }[/math], the three parameters Lorentzian function (note that it is not a density function and does not integrate to 1, as its amplitude [math]\displaystyle{ I }[/math] is 1 and not [math]\displaystyle{ 2/\pi \Gamma_\mathrm{res} }[/math]).
Examples
Examples of Fano resonances can be found in atomic physics, nuclear physics, condensed matter physics, electrical circuits, microwave engineering, nonlinear optics, nanophotonics, magnetic metamaterials,[5] and in mechanical waves.[6]
Fano can be observed with photoelectron spectroscopy[7] and Raman spectroscopy.[5] The phenomenon can be also observed at visible frequencies using simple glass microspheres, which may allow enhancing the magnetic field of light (which is typically small) by a few orders of magnitude.[8]
See also
References
- ↑ " A. Bianconi Ugo Fano and shape resonances in X-ray and Inner Shell Processes" AIP Conference Proceedings (2002): (19th Int. Conference Roma June 24–28, 2002) A. Bianconi arXiv: cond-mat/0211452 21 November 2002
- ↑ Fano, U. (15 December 1961). "Effects of Configuration Interaction on Intensities and Phase Shifts". Physical Review (American Physical Society (APS)) 124 (6): 1866–1878. doi:10.1103/physrev.124.1866. ISSN 0031-899X.
- ↑ Vittorini-Orgeas, Alessandra; Bianconi, Antonio (7 January 2009). "From Majorana Theory of Atomic Autoionization to Feshbach Resonances in High Temperature Superconductors". Journal of Superconductivity and Novel Magnetism 22 (3): 215–221. doi:10.1007/s10948-008-0433-x. ISSN 1557-1939.
- ↑ Limonov, Mikhail F.; Rybin, Mikhail V.; Poddubny, Alexander N.; Kivshar, Yuri S. (2017). "Fano resonances in photonics". Nature Photonics 11: 543-554. doi:10.1038/nphoton.2017.142.
- ↑ 5.0 5.1 Luk'yanchuk, Boris; Zheludev, Nikolay I.; Maier, Stefan A.; Halas, Naomi J.; Nordlander, Peter; Giessen, Harald; Chong, Chong Tow (23 August 2010). "The Fano resonance in plasmonic nanostructures and metamaterials". Nature Materials (Springer Nature) 9 (9): 707–715. doi:10.1038/nmat2810. ISSN 1476-1122. PMID 20733610.
- ↑ Martínez-Argüello, A. M.; Martínez-Mares, M.; Cobián-Suárez, M.; Báez, G.; Méndez-Sánchez, R. A. (1 May 2015). "A new Fano resonance in measurement processes". EPL (Europhysics Letters) 110 (5): 54003. doi:10.1209/0295-5075/110/54003. ISSN 0295-5075.
- ↑ Tjernberg, O.; Söderholm, S.; Karlsson, U. O.; Chiaia, G.; Qvarford, M.; Nylén, H.; Lindau, I. (1996-04-15). "Resonant photoelectron spectroscopy on NiO" (in en). Physical Review B 53 (15): 10372–10376. doi:10.1103/PhysRevB.53.10372. ISSN 0163-1829. PMID 9982607. https://link.aps.org/doi/10.1103/PhysRevB.53.10372.
- ↑ Wang, Z.B.; Luk'yanchuk, B.S.; Yue, L.; Yan, B.; Monks, J.; Dhama, R.; Minin, O.V.; Minin, I.V. et al. (30 Dec 2019). "High order Fano resonances and giant magnetic fields in dielectric microspheres". Scientific Reports (Springer Nature Limited) 9 (1): 20293. doi:10.1038/s41598-019-56783-3. ISSN 2045-2322. PMID 31889112.
 |  |
