Physics:Field of view
The field of view (FOV) is the angular extent of the observable world that is seen at any given moment. In the case of optical instruments or sensors, it is a solid angle through which a detector is sensitive to electromagnetic radiation. It is further relevant in photography.
Humans and animals
In the context of human and primate vision, the term "field of view" is typically only used in the sense of a restriction to what is visible by external apparatus, like when wearing spectacles[2] or virtual reality goggles. Note that eye movements are allowed in the definition but do not change the field of view when understood this way.
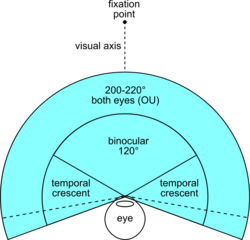
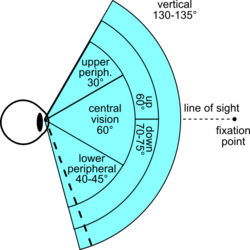
If the analogy of the eye's retina working as a sensor is drawn upon, the corresponding concept in human (and much of animal vision) is the visual field.[3] It is defined as "the number of degrees of visual angle during stable fixation of the eyes".[4] Note that eye movements are excluded in the visual field's definition. Humans have a slightly over 210-degree forward-facing horizontal arc of their visual field (i.e. without eye movements),[5][6] (with eye movements included it is slightly larger, as you can try for yourself by wiggling a finger on the side), while some birds have a complete or nearly complete 360-degree visual field. The vertical range of the visual field in humans is around 150 degrees.[5]
The range of visual abilities is not uniform across the visual field, and by implication the FoV, and varies between species. For example, binocular vision, which is the basis for stereopsis and is important for depth perception, covers 114 degrees (horizontally) of the visual field in humans;[7] the remaining peripheral 40 degrees on each side have no binocular vision (because only one eye can see those parts of the visual field). Some birds have a scant 10 to 20 degrees of binocular vision.
Similarly, color vision and the ability to perceive shape and motion vary across the visual field; in humans color vision and form perception are concentrated in the center of the visual field, while motion perception is only slightly reduced in the periphery and thus has a relative advantage there. The physiological basis for that is the much higher concentration of color-sensitive cone cells and color-sensitive parvocellular retinal ganglion cells in the fovea – the central region of the retina, together with a larger representation in the visual cortex – in comparison to the higher concentration of color-insensitive rod cells and motion-sensitive magnocellular retinal ganglion cells in the visual periphery, and smaller cortical representation. Since rod cells require considerably less light to be activated, the result of this distribution is further that peripheral vision is much more sensitive at night relative to foveal vision (sensitivity is highest at around 20 deg eccentricity).[3]
Conversions
Many optical instruments, particularly binoculars or spotting scopes, are advertised with their field of view specified in one of two ways: angular field of view, and linear field of view. Angular field of view is typically specified in degrees, while linear field of view is a ratio of lengths. For example, binoculars with a 5.8 degree (angular) field of view might be advertised as having a (linear) field of view of 102 mm per meter. As long as the FOV is less than about 10 degrees or so, the following approximation formulas allow one to convert between linear and angular field of view. Let [math]\displaystyle{ A }[/math] be the angular field of view in degrees. Let [math]\displaystyle{ M }[/math] be the linear field of view in millimeters per meter. Then, using the small-angle approximation:
- [math]\displaystyle{ A \approx {360^{\circ}\over 2 \pi} \cdot {M\over 1000 } \approx 0.0573 \times M }[/math]
- [math]\displaystyle{ M \approx {2 \pi \cdot 1000 \over 360^{\circ}} \cdot A \approx 17.45 \times A }[/math]
Machine vision
In machine vision the lens focal length and image sensor size sets up the fixed relationship between the field of view and the working distance. Field of view is the area of the inspection captured on the camera’s imager. The size of the field of view and the size of the camera’s imager directly affect the image resolution (one determining factor in accuracy). Working distance is the distance between the back of the lens and the target object.
Tomography
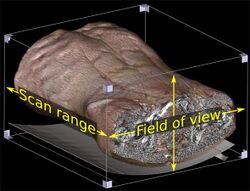
In tomography, the field of view is the area of each tomogram. In for example computed tomography, a volume of voxels can be created from such tomograms by merging multiple slices along the scan range.
Remote sensing
In remote sensing, the solid angle through which a detector element (a pixel sensor) is sensitive to electromagnetic radiation at any one time, is called instantaneous field of view or IFOV. A measure of the spatial resolution of a remote sensing imaging system, it is often expressed as dimensions of visible ground area, for some known sensor altitude.[8][9] Single pixel IFOV is closely related to concept of resolved pixel size, ground resolved distance, ground sample distance and modulation transfer function.
Astronomy
In astronomy, the field of view is usually expressed as an angular area viewed by the instrument, in square degrees, or for higher magnification instruments, in square arc-minutes. For reference the Wide Field Channel on the Advanced Camera for Surveys on the Hubble Space Telescope has a field of view of 10 sq. arc-minutes, and the High Resolution Channel of the same instrument has a field of view of 0.15 sq. arc-minutes. Ground-based survey telescopes have much wider fields of view. The photographic plates used by the UK Schmidt Telescope had a field of view of 30 sq. degrees. The 1.8 m (71 in) Pan-STARRS telescope, with the most advanced digital camera to date has a field of view of 7 sq. degrees. In the near infra-red WFCAM on UKIRT has a field of view of 0.2 sq. degrees and the VISTA telescope has a field of view of 0.6 sq. degrees. Until recently digital cameras could only cover a small field of view compared to photographic plates, although they beat photographic plates in quantum efficiency, linearity and dynamic range, as well as being much easier to process.
Photography
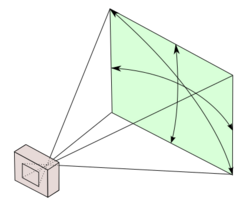
In photography, the field of view is that part of the world that is visible through the camera at a particular position and orientation in space; objects outside the FOV when the picture is taken are not recorded in the photograph. It is most often expressed as the angular size of the view cone, as an angle of view. For a normal lens, the diagonal (or horizontal or vertical) field of view can be calculated as:
- [math]\displaystyle{ \mathrm{FOV} = 2 \times \arctan\left(\frac{\text{sensor size}}{2f}\right) }[/math]
where [math]\displaystyle{ f }[/math] is the focal length, here the sensor size and [math]\displaystyle{ f }[/math] are in the same unit of length, FOV is in radians.
Microscopy
In microscopy, the field of view in high power (usually a 400-fold magnification when referenced in scientific papers) is called a high-power field, and is used as a reference point for various classification schemes.
For an objective with magnification [math]\displaystyle{ m }[/math], the FOV is related to the Field Number (FN) by
- [math]\displaystyle{ \mathrm{FOV} = \frac{\mathrm{FN}}{m}, }[/math]
if other magnifying lenses are used in the system (in addition to the objective), the total [math]\displaystyle{ m }[/math] for the projection is used.
Video games
The field of view in video games refers to the field of view of the camera looking at the game world, which is dependent on the scaling method used.
See also
- Field of regard
- Panorama
- Perimetry
- Peripheral vision
- Visual perception
- Useful field of view
- 35 mm equivalent focal length
- Angle of view
- Crop factor
- Image sensor format
- Line of sight
References
- ↑ "Cascading Milky Way". ESO Picture of the Week. http://www.eso.org/public/images/potw1224a/.
- ↑ Alfano, P.L.; Michel, G.F. (1990). "Restricting the field of view: Perceptual and performance effects". Perceptual and Motor Skills 70 (1): 35–45. doi:10.2466/pms.1990.70.1.35. PMID 2326136.
- ↑ 3.0 3.1 Strasburger, Hans; Rentschler, Ingo; Jüttner, Martin (2011). "Peripheral vision and pattern recognition: a review". Journal of Vision 11 (5): 1–82. doi:10.1167/11.5.13. PMID 22207654. http://www.journalofvision.org/content/11/5/13.
- ↑ Strasburger, Hans; Pöppel, Ernst (2002). Visual Field. In G. Adelman & B.H. Smith (Eds): Encyclopedia of Neuroscience; 3rd edition, on CD-ROM. Elsevier Science B.V., Amsterdam, New York.
- ↑ 5.0 5.1 Traquair, Harry Moss (1938). An Introduction to Clinical Perimetry, Chpt. 1. London: Henry Kimpton. pp. 4–5.
- ↑ Strasburger, Hans (2020). "Seven myths on crowding and peripheral vision". i-Perception 11 (2): 1–45. doi:10.1177/2041669520913052. PMID 32489576. PMC 7238452. https://doi.org/10.1177/2041669520913052.
- ↑ Howard, Ian P.; Rogers, Brian J. (1995). Binocular vision and stereopsis. New York: Oxford University Press. p. 32. ISBN 0-19-508476-4. https://books.google.com/books?id=I8vqITdETe0C&pg=PA32. Retrieved 3 June 2014.
- ↑ Oxford Reference. "Quick Reference: instantaneous field of view". Oxford University Press. http://www.oxfordreference.com/view/10.1093/oi/authority.20110803100005771.
- ↑ Wynne, James B. Campbell, Randolph H. (2011). Introduction to remote sensing (5th ed.). New York: Guilford Press. p. 261. ISBN 978-1609181765. https://books.google.com/books?id=NkLmDjSS8TsC.
 |  |
