Physics:Flexural modulus
In mechanics, the flexural modulus or bending modulus[1] is an intensive property that is computed as the ratio of stress to strain in flexural deformation, or the tendency for a material to resist bending. It is determined from the slope of a stress-strain curve produced by a flexural test (such as the ASTM D790), and uses units of force per area.[2] The flexural modulus defined using the 2-point (cantilever) and 3-point bend tests assumes a linear stress strain response.[3]
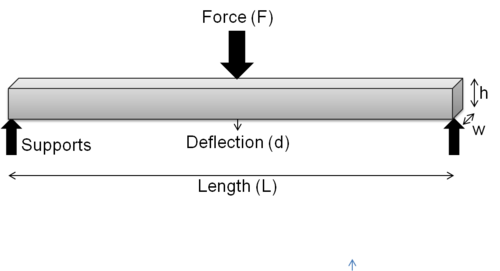
For a 3-point test of a rectangular beam behaving as an isotropic linear material, where w and h are the width and height of the beam, I is the second moment of area of the beam's cross-section, L is the distance between the two outer supports, and d is the deflection due to the load F applied at the middle of the beam, the flexural modulus:[1]
- [math]\displaystyle{ E_{\mathrm{flex}} = \frac {L^3 F}{4 w h^3 d} }[/math]
From elastic beam theory
- [math]\displaystyle{ d = \frac {L^3 F}{48 I E } }[/math]
and for rectangular beam
- [math]\displaystyle{ I = \frac{1}{12}wh^3 }[/math]
thus [math]\displaystyle{ E_{\mathrm{flex}} = E }[/math] (Elastic modulus)
For very small strains in isotropic materials – like glass, metal or polymer – flexural or bending modulus of elasticity is equivalent to the tensile modulus (Young's modulus) or compressive modulus of elasticity. However, in anisotropic materials, for example wood, these values may not be equivalent. Moreover, composite materials like fiber-reinforced polymers[4][3] or biological tissues[5] are inhomogeneous combinations of two or more materials, each with different material properties, therefore their tensile, compressive, and flexural moduli usually are not equivalent.
Related pages
References
- ↑ 1.0 1.1 Zweben, C.; W. S. Smith; M. W. Wardle (1979), "Test methods for fiber tensile strength, composite flexural modulus, and properties of fabric-reinforced laminates", Composite Materials: Testing and Design (Fifth Conference) (ASTM International): 228–228–35, doi:10.1520/STP36912S, ISBN 978-0-8031-4495-8
- ↑ D790-03: Standard Test Methods for Flexural Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materials, West Conshohocken, PA: ASTM International, 2003
- ↑ 3.0 3.1 Askeland, Donald R. (2016). The science and engineering of materials. Wright, Wendelin J. (Seventh ed.). Boston, MA. pp. 200. ISBN 978-1-305-07676-1. OCLC 903959750. https://www.worldcat.org/oclc/903959750.
- ↑ Tsai, S. W. (December 1979). Composite Materials, Testing and Design. ASTM. pp. 247. ISBN 9780803103078.
- ↑ Chahine, Nadeen O.; Wang, Christopher C-B.; Hung, Clark T.; Ateshian, Gerard A. (August 2004). "Anisotropic strain-dependent material properties of bovine articular cartilage in the transitional range from tension to compression". Journal of Biomechanics 37 (8): 1251–1261. doi:10.1016/j.jbiomech.2003.12.008. ISSN 0021-9290. PMID 15212931.
 |  |
