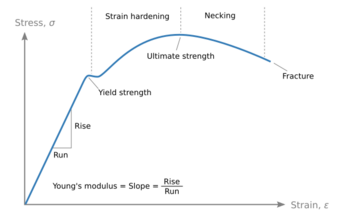
Physics:Young's modulus
Young's modulus (or Young modulus) is a mechanical property of solid materials that measures the tensile or compressive stiffness when the force is applied lengthwise. It is the modulus of elasticity for tension or axial compression. Young's modulus is defined as the ratio of the stress (force per unit area) applied to the object and the resulting axial strain (displacement or deformation) in the linear elastic region of the material.
Although Young's modulus is named after the 19th-century British scientist Thomas Young, the concept was developed in 1727 by Leonhard Euler. The first experiments that used the concept of Young's modulus in its modern form were performed by the Italian scientist Giordano Riccati in 1782, pre-dating Young's work by 25 years.[1] The term modulus is derived from the Latin root term modus which means measure.
Definition
Young's modulus, [math]\displaystyle{ E }[/math], quantifies the relationship between tensile or compressive stress [math]\displaystyle{ \sigma }[/math] (force per unit area) and axial strain [math]\displaystyle{ \varepsilon }[/math] (proportional deformation) in the linear elastic region of a material:[2] [math]\displaystyle{ E = \frac{\sigma}{\varepsilon} }[/math]
Young's modulus is commonly measured in the International System of Units (SI) in multiples of the pascal (Pa) and common values are in the range of gigapascals (GPa).
Examples:
- Rubber (increasing pressure: length increases quickly, meaning low [math]\displaystyle{ E }[/math])
- Aluminium (increasing pressure: length increases slowly, meaning high [math]\displaystyle{ E }[/math])
Linear elasticity
A solid material undergoes elastic deformation when a small load is applied to it in compression or extension. Elastic deformation is reversible, meaning that the material returns to its original shape after the load is removed.
At near-zero stress and strain, the stress–strain curve is linear, and the relationship between stress and strain is described by Hooke's law that states stress is proportional to strain. The coefficient of proportionality is Young's modulus. The higher the modulus, the more stress is needed to create the same amount of strain; an idealized rigid body would have an infinite Young's modulus. Conversely, a very soft material (such as a fluid) would deform without force, and would have zero Young's modulus.
Related but distinct properties
Material stiffness is a distinct property from the following:
- Strength: maximum amount of stress that material can withstand while staying in the elastic (reversible) deformation regime;
- Geometric stiffness: a global characteristic of the body that depends on its shape, and not only on the local properties of the material; for instance, an I-beam has a higher bending stiffness than a rod of the same material for a given mass per length;
- Hardness: relative resistance of the material's surface to penetration by a harder body;
- Toughness: amount of energy that a material can absorb before fracture.
Usage
Young's modulus enables the calculation of the change in the dimension of a bar made of an isotropic elastic material under tensile or compressive loads. For instance, it predicts how much a material sample extends under tension or shortens under compression. The Young's modulus directly applies to cases of uniaxial stress; that is, tensile or compressive stress in one direction and no stress in the other directions. Young's modulus is also used in order to predict the deflection that will occur in a statically determinate beam when a load is applied at a point in between the beam's supports.
Other elastic calculations usually require the use of one additional elastic property, such as the shear modulus [math]\displaystyle{ G }[/math], bulk modulus [math]\displaystyle{ K }[/math], and Poisson's ratio [math]\displaystyle{ \nu }[/math]. Any two of these parameters are sufficient to fully describe elasticity in an isotropic material. For homogeneous isotropic materials simple relations exist between elastic constants that allow calculating them all as long as two are known:
- [math]\displaystyle{ E = 2G(1+\nu) = 3K(1-2\nu). }[/math]
Linear versus non-linear
Young's modulus represents the factor of proportionality in Hooke's law, which relates the stress and the strain. However, Hooke's law is only valid under the assumption of an elastic and linear response. Any real material will eventually fail and break when stretched over a very large distance or with a very large force; however, all solid materials exhibit nearly Hookean behavior for small enough strains or stresses. If the range over which Hooke's law is valid is large enough compared to the typical stress that one expects to apply to the material, the material is said to be linear. Otherwise (if the typical stress one would apply is outside the linear range), the material is said to be non-linear.
Steel, carbon fiber and glass among others are usually considered linear materials, while other materials such as rubber and soils are non-linear. However, this is not an absolute classification: if very small stresses or strains are applied to a non-linear material, the response will be linear, but if very high stress or strain is applied to a linear material, the linear theory will not be enough. For example, as the linear theory implies reversibility, it would be absurd to use the linear theory to describe the failure of a steel bridge under a high load; although steel is a linear material for most applications, it is not in such a case of catastrophic failure.
In solid mechanics, the slope of the stress–strain curve at any point is called the tangent modulus. It can be experimentally determined from the slope of a stress–strain curve created during tensile tests conducted on a sample of the material.
Directional materials
Young's modulus is not always the same in all orientations of a material. Most metals and ceramics, along with many other materials, are isotropic, and their mechanical properties are the same in all orientations. However, metals and ceramics can be treated with certain impurities, and metals can be mechanically worked to make their grain structures directional. These materials then become anisotropic, and Young's modulus will change depending on the direction of the force vector.[3] Anisotropy can be seen in many composites as well. For example, carbon fiber has a much higher Young's modulus (is much stiffer) when force is loaded parallel to the fibers (along the grain). Other such materials include wood and reinforced concrete. Engineers can use this directional phenomenon to their advantage in creating structures.
Temperature dependence
The Young's modulus of metals varies with the temperature and can be realized through the change in the interatomic bonding of the atoms, and hence its change is found to be dependent on the change in the work function of the metal. Although classically, this change is predicted through fitting and without a clear underlying mechanism (for example, the Watchman's formula), the Rahemi-Li model[4] demonstrates how the change in the electron work function leads to change in the Young's modulus of metals and predicts this variation with calculable parameters, using the generalization of the Lennard-Jones potential to solids. In general, as the temperature increases, the Young's modulus decreases via [math]\displaystyle{ E(T) = \beta(\varphi(T))^6 }[/math] where the electron work function varies with the temperature as [math]\displaystyle{ \varphi(T)=\varphi_0-\gamma\frac{(k_BT)^2}{\varphi_0} }[/math] and [math]\displaystyle{ \gamma }[/math] is a calculable material property which is dependent on the crystal structure (for example, BCC, FCC). [math]\displaystyle{ \varphi_0 }[/math] is the electron work function at T=0 and [math]\displaystyle{ \beta }[/math] is constant throughout the change.
Calculation
Young's modulus E, is calculated by dividing the tensile stress, [math]\displaystyle{ \sigma(\varepsilon) }[/math], by the engineering extensional strain, [math]\displaystyle{ \varepsilon }[/math], in the elastic (initial, linear) portion of the physical stress–strain curve:
[math]\displaystyle{ E \equiv \frac{\sigma(\varepsilon)}{\varepsilon}= \frac{F/A}{\Delta L/L_0} = \frac{F L_0} {A \, \Delta L} }[/math] where
- [math]\displaystyle{ E }[/math] is the Young's modulus (modulus of elasticity)
- [math]\displaystyle{ F }[/math] is the force exerted on an object under tension;
- [math]\displaystyle{ A }[/math] is the actual cross-sectional area, which equals the area of the cross-section perpendicular to the applied force;
- [math]\displaystyle{ \Delta L }[/math] is the amount by which the length of the object changes ([math]\displaystyle{ \Delta L }[/math] is positive if the material is stretched, and negative when the material is compressed);
- [math]\displaystyle{ L_0 }[/math] is the original length of the object.
Force exerted by stretched or contracted material
Young's modulus of a material can be used to calculate the force it exerts under specific strain.
- [math]\displaystyle{ F = \frac{E A \, \Delta L} {L_0} }[/math]
where [math]\displaystyle{ F }[/math] is the force exerted by the material when contracted or stretched by [math]\displaystyle{ \Delta L }[/math].
Hooke's law for a stretched wire can be derived from this formula:
- [math]\displaystyle{ F = \left( \frac{E A} {L_0} \right) \, \Delta L = k x }[/math]
where it comes in saturation
- [math]\displaystyle{ k \equiv \frac {E A} {L_0} \, }[/math] and [math]\displaystyle{ x \equiv \Delta L. }[/math]
But note that the elasticity of coiled springs comes from shear modulus, not Young's modulus. [citation needed]
Elastic potential energy
The elastic potential energy stored in a linear elastic material is given by the integral of the Hooke's law:
- [math]\displaystyle{ U_e = \int {k x}\, dx = \frac {1} {2} k x^2. }[/math]
now by explicating the intensive variables:
- [math]\displaystyle{ U_e = \int \frac{E A \, \Delta L} {L_0}\, d\Delta L = \frac {E A} {L_0} \int \Delta L \, d\Delta L = \frac {E A \, {\Delta L}^2} {2 L_0} }[/math]
This means that the elastic potential energy density (that is, per unit volume) is given by:
- [math]\displaystyle{ \frac{U_e} {A L_0} = \frac {E \, {\Delta L}^2} {2 L_0^2} }[/math]
or, in simple notation, for a linear elastic material: [math]\displaystyle{ u_e(\varepsilon) = \int {E \, \varepsilon}\, d\varepsilon = \frac {1} {2} E {\varepsilon}^2 }[/math], since the strain is defined [math]\displaystyle{ \varepsilon \equiv \frac {\Delta L} {L_0} }[/math].
In a nonlinear elastic material the Young's modulus is a function of the strain, so the second equivalence no longer holds, and the elastic energy is not a quadratic function of the strain:
- [math]\displaystyle{ u_e(\varepsilon) = \int E(\varepsilon) \, \varepsilon \, d\varepsilon \ne \frac {1} {2} E \varepsilon^2 }[/math]
Examples
Young's modulus can vary somewhat due to differences in sample composition and test method. The rate of deformation has the greatest impact on the data collected, especially in polymers. The values here are approximate and only meant for relative comparison.
| Material | Young's modulus (GPa) | Megapound per square inch (Mpsi)[5] | Ref. |
|---|---|---|---|
| Aluminium (13Al) | 68 | 9.86 | [6][7][8][9][10][11] |
| Amino-acid molecular crystals | 21–44 | 3.05–6.38 | [12] |
| Aramid (for example, Kevlar) | 70.5–112.4 | 10.2–16.3 | [13] |
| Aromatic peptide-nanospheres | 230–275 | 33.4–39.9 | [14] |
| Aromatic peptide-nanotubes | 19–27 | 2.76–3.92 | [15][16] |
| Bacteriophage capsids | 1–3 | 0.145–0.435 | [17] |
| Beryllium (4Be) | 287 | 41.6 | [18] |
| Bone, human cortical | 14 | 2.03 | [19] |
| Brass | 106 | 15.4 | [20] |
| Bronze | 112 | 16.2 | [21] |
| Carbon nitride (CN2) | 822 | 119 | [22] |
| Carbon-fiber-reinforced plastic (CFRP), 50/50 fibre/matrix, biaxial fabric | 30–50 | 4.35–7.25 | [23] |
| Carbon-fiber-reinforced plastic (CFRP), 70/30 fibre/matrix, unidirectional, along fibre | 181 | 26.3 | [24] |
| Cobalt-chrome (CoCr) | 230 | 33.4 | [25] |
| Copper (Cu), annealed | 110 | 16 | [26] |
| Diamond (C), synthetic | 1050–1210 | 152–175 | [27] |
| Diatom frustules, largely silicic acid | 0.35–2.77 | 0.051–0.058 | [28] |
| Flax fiber | 58 | 8.41 | [29] |
| Float glass | 47.7–83.6 | 6.92–12.1 | [30] |
| Glass-reinforced polyester (GRP) | 17.2 | 2.49 | [31] |
| Gold | 77.2 | 11.2 | [32] |
| Graphene | 1050 | 152 | [33] |
| Hemp fiber | 35 | 5.08 | [34] |
| High-density polyethylene (HDPE) | 0.97–1.38 | 0.141–0.2 | [35] |
| High-strength concrete | 30 | 4.35 | [36] |
| Lead (82Pb), chemical | 13 | 1.89 | [11] |
| Low-density polyethylene (LDPE), molded | 0.228 | 0.0331 | [37] |
| Magnesium alloy | 45.2 | 6.56 | [38] |
| Medium-density fiberboard (MDF) | 4 | 0.58 | [39] |
| Molybdenum (Mo), annealed | 330 | 47.9 | [40][7][8][9][10][11] |
| Monel | 180 | 26.1 | [11] |
| Mother-of-pearl (largely calcium carbonate) | 70 | 10.2 | [41] |
| Nickel (28Ni), commercial | 200 | 29 | [11] |
| Nylon 66 | 2.93 | 0.425 | [42] |
| Osmium (76Os) | 525–562 | 76.1–81.5 | [43] |
| Osmium nitride (OsN2) | 194.99–396.44 | 28.3–57.5 | [44] |
| Polycarbonate (PC) | 2.2 | 0.319 | [45] |
| Polyethylene terephthalate (PET), unreinforced | 3.14 | 0.455 | [46] |
| Polypropylene (PP), molded | 1.68 | 0.244 | [47] |
| Polystyrene, crystal | 2.5–3.5 | 0.363–0.508 | [48] |
| Polystyrene, foam | 0.0025–0.007 | 0.000363–0.00102 | [49] |
| Polytetrafluoroethylene (PTFE), molded | 0.564 | 0.0818 | [50] |
| Rubber, small strain | 0.01–0.1 | 0.00145–0.0145 | [12] |
| Silicon, single crystal, different directions | 130–185 | 18.9–26.8 | [51] |
| Silicon carbide (SiC) | 90–137 | 13.1–19.9 | [52] |
| Single-walled carbon nanotube | [math]\displaystyle{ \gt }[/math]1000 | [math]\displaystyle{ \gt }[/math]140 | |
| Steel, A36 | 200 | 29 | [53] |
| Stinging nettle fiber | 87 | 12.6 | [29] |
| Titanium (22Ti) | 116 | 16.8 | [54][55][7][9][8][11][10] |
| Titanium alloy, Grade 5 | 114 | 16.5 | [56] |
| Tooth enamel, largely calcium phosphate | 83 | 12 | [57] |
| Tungsten carbide (WC) | 600–686 | 87–99.5 | [58] |
| Wood, American beech | 9.5–11.9 | 1.38–1.73 | [59] |
| Wood, black cherry | 9–10.3 | 1.31–1.49 | [59] |
| Wood, red maple | 9.6–11.3 | 1.39–1.64 | [59] |
| Wrought iron | 193 | 28 | [60] |
| Yttrium iron garnet (YIG), polycrystalline | 193 | 28 | [61] |
| Yttrium iron garnet (YIG), single-crystal | 200 | 29 | [62] |
| Zinc (30Zn) | 108 | 15.7 | [63] |
| Zirconium (40Zr), commercial | 95 | 13.8 | [11] |
See also
- Bending stiffness
- Deflection
- Deformation
- Flexural modulus
- Impulse excitation technique
- List of materials properties
- Yield (engineering)
References
- ↑ The Rational mechanics of Flexible or Elastic Bodies, 1638–1788: Introduction to Leonhardi Euleri Opera Omnia, vol. X and XI, Seriei Secundae. Orell Fussli.
- ↑ Jastrzebski, D. (1959). Nature and Properties of Engineering Materials (Wiley International ed.). John Wiley & Sons, Inc.
- ↑ Gorodtsov, V.A.; Lisovenko, D.S. (2019). "Extreme values of Young's modulus and Poisson's ratio of hexagonal crystals" (in en). Mechanics of Materials 134: 1–8. doi:10.1016/j.mechmat.2019.03.017.
- ↑ Rahemi, Reza; Li, Dongyang (April 2015). "Variation in electron work function with temperature and its effect on the Young's modulus of metals". Scripta Materialia 99 (2015): 41–44. doi:10.1016/j.scriptamat.2014.11.022. Bibcode: 2015arXiv150308250R.
- ↑ "Unit of Measure Converter". http://www.matweb.com/tools/unitconverter.aspx.
- ↑ "Aluminum, Al". http://www.matweb.com/search/DataSheet.aspx?MatGUID=0cd1edf33ac145ee93a0aa6fc666c0e0.
- ↑ 7.0 7.1 7.2 Weast, Robert C. (1981). CRC Handbook of Chemistry and Physics (62nd ed.). Boca Raton, FL: CRC Press. doi:10.1002/jctb.280500215. ISBN 978-0-84-930740-9.
- ↑ 8.0 8.1 8.2 Ross, Robert B. (1992). Metallic Materials Specification Handbook (4th ed.). London: Chapman & Hall. doi:10.1007/978-1-4615-3482-2. ISBN 9780412369407.
- ↑ 9.0 9.1 9.2 Nunes, Rafael; Adams, J. H.; Ammons, Mitchell et al. (1990). Volume 2: Properties and Selection: Nonferrous Alloys and Special-Purpose Materials. ASM Handbook (10th ed.). ASM International. ISBN 978-0-87170-378-1. http://sme.vimaru.edu.vn/sites/sme.vimaru.edu.vn/files/volume_2_-_properties_and_selection_nonf.pdf.
- ↑ 10.0 10.1 10.2 Nayar, Alok (1997). The Metals Databook. New York, NY: McGraw-Hill. ISBN 978-0-07-462300-8.
- ↑ 11.0 11.1 11.2 11.3 11.4 11.5 11.6 Lide, David R., ed (1999). "Commercial Metals and Alloys". CRC Handbook of Chemistry and Physics (80th ed.). Boca Raton, FL: CRC Press. ISBN 978-0-84-930480-4.
- ↑ 12.0 12.1 Azuri, Ido; Meirzadeh, Elena; Ehre, David et al. (November 9, 2015). "Unusually Large Young's Moduli of Amino Acid Molecular Crystals". Angewandte Chemie (Wiley) 54 (46): 13566–13570. doi:10.1002/anie.201505813. PMID 26373817. http://www.sas.upenn.edu/rappegroup/publications/Papers/Azuri15p13566.pdf.
- ↑ "Kevlar Aramid Fiber Technical Guide". 2017. https://www.dupont.com/content/dam/dupont/amer/us/en/safety/public/documents/en/Kevlar_Technical_Guide_0319.pdf.
- ↑ Adler-Abramovich, Lihi; Kol, Nitzan; Yanai, Inbal et al. (December 17, 2010). "Self-Assembled Organic Nanostructures with Metallic-Like Stiffness". Angewandte Chemie (Wiley-VCH) 49 (51): 9939–9942. September 28, 2010. doi:10.1002/anie.201002037. PMID 20878815.
- ↑ Kol, Nitzan; Adler-Abramovich, Lihi; Barlam, David et al. (June 8, 2005). "Self-Assembled Peptide Nanotubes Are Uniquely Rigid Bioinspired Supramolecular Structures". Nano Letters (Israel: American Chemical Society) 5 (7): 1343–1346. doi:10.1021/nl0505896. PMID 16178235. Bibcode: 2005NanoL...5.1343K. https://pubs.acs.org/doi/full/10.1021/nl0505896.
- ↑ Niu, Lijiang; Chen, Xinyong; Allen, Stephanie et al. (June 6, 2007). "Using the Bending Beam Model to Estimate the Elasticity of Diphenylalanine Nanotubes". Langmuir (American Chemical Society) 23 (14): 7443–7446. doi:10.1021/la7010106. PMID 17550276. https://pubs.acs.org/doi/full/10.1021/la7010106.
- ↑ Ivanovska, Irena L.; de Pablo, Pedro J.; Ibarra, Benjamin et al. (May 7, 2004). Lubensky, Tom C.. ed. "Bacteriophage capsids: Tough nanoshells with complex elastic properties". Proceedings of the National Academy of Sciences of the United States of America (The National Academy of Sciences) 101 (20): 7600–7605. doi:10.1073/pnas.0308198101. PMID 15133147. Bibcode: 2004PNAS..101.7600I.
- ↑ Foley, James C.; Abeln, Stephen P.; Stanek, Paul W. et al. (2010). "An Overview of Current Research and Industrial Practices of be Powder Metallurgy". in Marquis, Fernand D. S.. Powder Materials: Current Research and Industrial Practices III. Hoboken, NJ: John Wiley & Sons, Inc.. pp. 263. doi:10.1002/9781118984239.ch32. ISBN 978-1-11-898423-9.
- ↑ Rho, Jae Young; Ashman, Richard B.; Turner, Charles H. (February 1993). "Young's modulus of trabecular and cortical bone material: Ultrasonic and microtensile measurements". Journal of Biomechanics (Elsevier) 26 (2): 111–119. doi:10.1016/0021-9290(93)90042-d. PMID 8429054. https://www.sciencedirect.com/science/article/abs/pii/002192909390042D.
- ↑ "Overview of materials for Brass". http://www.matweb.com/search/DataSheet.aspx?MatGUID=d3bd4617903543ada92f4c101c2a20e5.
- ↑ "Overview of materials for Bronze". http://www.matweb.com/search/datasheet.aspx?MatGUID=66575ff2cd5249c49d76df15b47dbca4.
- ↑ Chowdhury, Shafiul; Laugier, Michael T.; Rahman, Ismet Zakia (April–August 2004). "Measurement of the mechanical properties of carbon nitride thin films from the nanoindentation loading curve". Diamond and Related Materials 13 (4–8): 1543–1548. doi:10.1016/j.diamond.2003.11.063. Bibcode: 2004DRM....13.1543C.
- ↑ Summerscales, John (September 11, 2019). "Composites Design and Manufacture (Plymouth University teaching support materials)". University of Plymouth. https://www.fose1.plymouth.ac.uk/sme/MATS347/MATS347A2%20E-G-nu.htm#E.
- ↑ Kopeliovich, Dmitri (June 3, 2012). "Epoxy Matrix Composite reinforced by 70% carbon fibers". http://www.substech.com/dokuwiki/doku.php?id=epoxy_matrix_composite_reinforced_by_70_carbon_fibers.
- ↑ Bose, Susmita; Banerjee, Dishary; Bandyopadhyay, Amit (2016). "Introduction to Biomaterials and Devices for Bone Disorders". in Bose, Susmita. Materials for Bone Disorders. Academic Press. pp. 1–27. doi:10.1016/B978-0-12-802792-9.00001-X. ISBN 978-0-12-802792-9.
- ↑ "Copper, Cu; Annealed". http://www.matweb.com/search/DataSheet.aspx?MatGUID=9aebe83845c04c1db5126fada6f76f7e.
- ↑ Spear, Karl E., ed (1994). Synthetic Diamond: Emerging CVD Science and Technology. Wiley. pp. 315. ISBN 978-0-47-153589-8.
- ↑ Subhash, Ghatu; Yao, Shuhuai; Bellinger, Brent; Gretz, Michael R. (January 2005). "Investigation of mechanical properties of diatom frustules using nanoindentation". Journal of Nanoscience and Nanotechnology (American Scientific Publishers) 5 (1): 50–56. doi:10.1166/jnn.2005.006. PMID 15762160.
- ↑ 29.0 29.1 Bodros, Edwin; Baley, Christophe (May 15, 2008). "Study of the tensile properties of stinging nettle fibres (Urtica dioica)". Materials Letters 62 (14): 2143–2145. doi:10.1016/j.matlet.2007.11.034.
- ↑ "Float glass – Properties and Applications". February 16, 2001. https://www.azom.com/properties.aspx?ArticleID=89.
- ↑ Kopeliovich, Dmitri (March 6, 2012). "Polyester Matrix Composite reinforced by glass fibers (Fiberglass)". http://www.substech.com/dokuwiki/doku.php?id=polyester_matrix_composite_reinforced_by_glass_fibers_fiberglass.
- ↑ "Gold material property data". http://www.matweb.com/search/DataSheet.aspx?MatGUID=d2a2119a08904a0fa706e9408cddb88e. Retrieved September 8, 2021.
- ↑ Liu, Fang; Ming, Pingbing; Li, Ju (August 28, 2007). "Ab initio calculation of ideal strength and phonon instability of graphene under tension". Physical Review B (American Physical Society) 76 (6): 064120. doi:10.1103/PhysRevB.76.064120. Bibcode: 2007PhRvB..76f4120L. http://li.mit.edu/A/Papers/07/Liu07.pdf.
- ↑ Saheb, Nabi; Jog, Jyoti (October 15, 1999). "Natural fibre polymer composites: a review". Advances in Polymer Technology (John Wiley & Sons, Inc.) 18 (4): 351–363. doi:10.1002/(SICI)1098-2329(199924)18:4<351::AID-ADV6>3.0.CO;2-X.
- ↑ "High-Density Polyethylene (HDPE)". Chemical Retrieval on the Web. https://polymerdatabase.com/Commercial%20Polymers/HDPE.html.
- ↑ Cardarelli, François (2008). "Cements, Concrete, Building Stones, and Construction Materials". Materials Handbook: A Concise Desktop Reference (2nd ed.). London: Springer-Verlag. pp. 1421–1439. doi:10.1007/978-3-319-38925-7_15. ISBN 978-3-319-38923-3.
- ↑ "Overview of materials for Low Density Polyethylene (LDPE), Molded". http://matweb.com/search/DataSheet.aspx?MatGUID=557b96c10e0843dbb1e830ceedeb35b0.
- ↑ "Overview of materials for Magnesium Alloy". http://www.matweb.com/search/DataSheet.aspx?MatGUID=4e6a4852b14c4b12998acf2f8316c07c.
- ↑ "Medium Density Fiberboard (MDF)". May 30, 2020. http://www.makeitfrom.com/data/?material=MDF.
- ↑ "Molybdenum, Mo, Annealed". http://www.matweb.com/search/datasheet.aspx?matguid=ef57c33963404798ad0301a05692312a.
- ↑ Jackson, Andrew P.; Vincent, Julian F. V.; Turner, R. M. (September 22, 1988). "The mechanical design of nacre". Proceedings of the Royal Society B (Royal Society) 234 (1277): 415–440. doi:10.1098/rspb.1988.0056. ISSN 0080-4649. Bibcode: 1988RSPSB.234..415J.
- ↑ "Nylon® 6/6 (Polyamide)". 2011. https://www.polytechindustrial.com/products/plastic-stock-shapes/nylon-66.
- ↑ Pandey, Dharmendra Kumar; Singh, Devraj; Yadawa, Pramod Kumar (April 2, 2009). "Ultrasonic Study of Osmium and Ruthenium". Platinum Metals Review (Johnson Matthey) 53 (4): 91–97. doi:10.1595/147106709X430927. http://www.technology.matthey.com/pdf/91-97-pmr-apr09.pdf. Retrieved May 7, 2021.
- ↑ Gaillac, Romain; Coudert, François-Xavier (July 26, 2020). "ELATE: Elastic tensor analysis". http://progs.coudert.name/elate/mp?query=mp-973935.
- ↑ "Polycarbonate". https://designerdata.nl/materials/plastics/thermo-plastics/polycarbonate.
- ↑ "Overview of materials for Polyethylene Terephthalate (PET), Unreinforced". http://www.matweb.com/search/DataSheet.aspx?MatGUID=a696bdcdff6f41dd98f8eec3599eaa20.
- ↑ "Overview of Materials for Polypropylene, Molded". http://www.matweb.com/search/DataSheet.aspx?MatGUID=08fb0f47ef7e454fbf7092517b2264b2.
- ↑ "Young's Modulus: Tensile Elasticity Units, Factors & Material Table". SpecialChem. https://omnexus.specialchem.com/polymer-properties/properties/young-modulus.
- ↑ "Technical Data – Application Recommendations Dimensioning Aids". BASF. August 2019. https://www.styrodur.com/portal/streamer?fid=1225078.
- ↑ "Overview of materials for Polytetrafluoroethylene (PTFE), Molded". http://www.matweb.com/search/datasheet_print.aspx?matguid=4d14eac958e5401a8fd152e1261b6843.
- ↑ Boyd, Euan J.; Uttamchandani, Deepak (2012). "Measurement of the Anisotropy of Young's Modulus in Single-Crystal Silicon". Journal of Microelectromechanical Systems (Institute of Electrical and Electronics Engineers) 21 (1): 243–249. doi:10.1109/JMEMS.2011.2174415. ISSN 1057-7157.
- ↑ "Silicon Carbide (SiC) Properties and Applications". February 5, 2001. https://www.azom.com/properties.aspx?ArticleID=42.
- ↑ "ASTM A36 Mild/Low Carbon Steel". July 5, 2012. https://www.azom.com/article.aspx?ArticleID=6117.
- ↑ "Titanium, Ti". http://www.matweb.com/search/datasheet.aspx?MatGUID=66a15d609a3f4c829cb6ad08f0dafc01.
- ↑ Boyer, Rodney, ed (1994). Materials Properties Handbook: Titanium Alloys. Materials Park, OH: ASM International. ISBN 978-0-87-170481-8.
- ↑ U.S. Titanium Industry Inc. (July 30, 2002). "Titanium Alloys – Ti6Al4V Grade 5". https://www.azom.com/article.aspx?ArticleID=1547.
- ↑ Staines, Michael; Robinson, W. H.; Hood, J. A. A. (September 1981). "Spherical indentation of tooth enamel". Journal of Materials Science (Springer) 16 (9): 2551–2556. doi:10.1007/bf01113595. Bibcode: 1981JMatS..16.2551S.
- ↑ "Tungsten Carbide – An Overview". January 21, 2002. https://www.azom.com/properties.aspx?ArticleID=1203.
- ↑ 59.0 59.1 59.2 Green, David W.; Winandy, Jerrold E.; Kretschmann, David E. (1999). "Mechanical Properties of Wood". Wood Handbook: Wood as an Engineering Material. Madison, WI: Forest Products Laboratory. pp. 4–8. https://www.fpl.fs.fed.us/documnts/fplgtr/fplgtr113/ch04.pdf.
- ↑ "Wrought Iron – Properties and Applications". August 13, 2013. https://www.azom.com/article.aspx?ArticleID=9555.
- ↑ Chou, Hung-Ming; Case, E. D. (November 1988). "Characterization of some mechanical properties of polycrystalline yttrium iron garnet (YIG) by non-destructive methods". Journal of Materials Science Letters 7 (11): 1217–1220. doi:10.1007/BF00722341.
- ↑ "Yttrium Iron Garnet". December 28, 2012. http://deltroniccrystalindustries.com/deltronic_crystal_products/yttrium_iron_garnet.
- ↑ "An Introduction to Zinc". July 23, 2001. https://www.azom.com/properties.aspx?ArticleID=602.
Further reading
- ASTM E 111, "Standard Test Method for Young's Modulus, Tangent Modulus, and Chord Modulus"
- The ASM Handbook (various volumes) contains Young's Modulus for various materials and information on calculations. Online version (Subscription content?)
External links
- Matweb: free database of engineering properties for over 115,000 materials
- Young's Modulus for groups of materials, and their cost
| Conversion formulae | |||||||
|---|---|---|---|---|---|---|---|
| Homogeneous isotropic linear elastic materials have their elastic properties uniquely determined by any two moduli among these; thus, given any two, any other of the elastic moduli can be calculated according to these formulas. | |||||||
| [math]\displaystyle{ K=\, }[/math] | [math]\displaystyle{ E=\, }[/math] | [math]\displaystyle{ \lambda=\, }[/math] | [math]\displaystyle{ G=\, }[/math] | [math]\displaystyle{ \nu=\, }[/math] | [math]\displaystyle{ M=\, }[/math] | Notes | |
| [math]\displaystyle{ (K,\,E) }[/math] | [math]\displaystyle{ \tfrac{3K(3K-E)}{9K-E} }[/math] | [math]\displaystyle{ \tfrac{3KE}{9K-E} }[/math] | [math]\displaystyle{ \tfrac{3K-E}{6K} }[/math] | [math]\displaystyle{ \tfrac{3K(3K+E)}{9K-E} }[/math] | |||
| [math]\displaystyle{ (K,\,\lambda) }[/math] | [math]\displaystyle{ \tfrac{9K(K-\lambda)}{3K-\lambda} }[/math] | [math]\displaystyle{ \tfrac{3(K-\lambda)}{2} }[/math] | [math]\displaystyle{ \tfrac{\lambda}{3K-\lambda} }[/math] | [math]\displaystyle{ 3K-2\lambda\, }[/math] | |||
| [math]\displaystyle{ (K,\,G) }[/math] | [math]\displaystyle{ \tfrac{9KG}{3K+G} }[/math] | [math]\displaystyle{ K-\tfrac{2G}{3} }[/math] | [math]\displaystyle{ \tfrac{3K-2G}{2(3K+G)} }[/math] | [math]\displaystyle{ K+\tfrac{4G}{3} }[/math] | |||
| [math]\displaystyle{ (K,\,\nu) }[/math] | [math]\displaystyle{ 3K(1-2\nu)\, }[/math] | [math]\displaystyle{ \tfrac{3K\nu}{1+\nu} }[/math] | [math]\displaystyle{ \tfrac{3K(1-2\nu)}{2(1+\nu)} }[/math] | [math]\displaystyle{ \tfrac{3K(1-\nu)}{1+\nu} }[/math] | |||
| [math]\displaystyle{ (K,\,M) }[/math] | [math]\displaystyle{ \tfrac{9K(M-K)}{3K+M} }[/math] | [math]\displaystyle{ \tfrac{3K-M}{2} }[/math] | [math]\displaystyle{ \tfrac{3(M-K)}{4} }[/math] | [math]\displaystyle{ \tfrac{3K-M}{3K+M} }[/math] | |||
| [math]\displaystyle{ (E,\,\lambda) }[/math] | [math]\displaystyle{ \tfrac{E + 3\lambda + R}{6} }[/math] | [math]\displaystyle{ \tfrac{E-3\lambda+R}{4} }[/math] | [math]\displaystyle{ \tfrac{2\lambda}{E+\lambda+R} }[/math] | [math]\displaystyle{ \tfrac{E-\lambda+R}{2} }[/math] | [math]\displaystyle{ R=\sqrt{E^2+9\lambda^2 + 2E\lambda} }[/math] | ||
| [math]\displaystyle{ (E,\,G) }[/math] | [math]\displaystyle{ \tfrac{EG}{3(3G-E)} }[/math] | [math]\displaystyle{ \tfrac{G(E-2G)}{3G-E} }[/math] | [math]\displaystyle{ \tfrac{E}{2G}-1 }[/math] | [math]\displaystyle{ \tfrac{G(4G-E)}{3G-E} }[/math] | |||
| [math]\displaystyle{ (E,\,\nu) }[/math] | [math]\displaystyle{ \tfrac{E}{3(1-2\nu)} }[/math] | [math]\displaystyle{ \tfrac{E\nu}{(1+\nu)(1-2\nu)} }[/math] | [math]\displaystyle{ \tfrac{E}{2(1+\nu)} }[/math] | [math]\displaystyle{ \tfrac{E(1-\nu)}{(1+\nu)(1-2\nu)} }[/math] | |||
| [math]\displaystyle{ (E,\,M) }[/math] | [math]\displaystyle{ \tfrac{3M-E+S}{6} }[/math] | [math]\displaystyle{ \tfrac{M-E+S}{4} }[/math] | [math]\displaystyle{ \tfrac{3M+E-S}{8} }[/math] | [math]\displaystyle{ \tfrac{E-M+S}{4M} }[/math] | [math]\displaystyle{ S=\pm\sqrt{E^2+9M^2-10EM} }[/math] There are two valid solutions. | ||
| [math]\displaystyle{ (\lambda,\,G) }[/math] | [math]\displaystyle{ \lambda+ \tfrac{2G}{3} }[/math] | [math]\displaystyle{ \tfrac{G(3\lambda + 2G)}{\lambda + G} }[/math] | [math]\displaystyle{ \tfrac{\lambda}{2(\lambda + G)} }[/math] | [math]\displaystyle{ \lambda+2G\, }[/math] | |||
| [math]\displaystyle{ (\lambda,\,\nu) }[/math] | [math]\displaystyle{ \tfrac{\lambda(1+\nu)}{3\nu} }[/math] | [math]\displaystyle{ \tfrac{\lambda(1+\nu)(1-2\nu)}{\nu} }[/math] | [math]\displaystyle{ \tfrac{\lambda(1-2\nu)}{2\nu} }[/math] | [math]\displaystyle{ \tfrac{\lambda(1-\nu)}{\nu} }[/math] | Cannot be used when [math]\displaystyle{ \nu=0 \Leftrightarrow \lambda=0 }[/math] | ||
| [math]\displaystyle{ (\lambda,\,M) }[/math] | [math]\displaystyle{ \tfrac{M + 2\lambda}{3} }[/math] | [math]\displaystyle{ \tfrac{(M-\lambda)(M+2\lambda)}{M+\lambda} }[/math] | [math]\displaystyle{ \tfrac{M-\lambda}{2} }[/math] | [math]\displaystyle{ \tfrac{\lambda}{M+\lambda} }[/math] | |||
| [math]\displaystyle{ (G,\,\nu) }[/math] | [math]\displaystyle{ \tfrac{2G(1+\nu)}{3(1-2\nu)} }[/math] | [math]\displaystyle{ 2G(1+\nu)\, }[/math] | [math]\displaystyle{ \tfrac{2 G \nu}{1-2\nu} }[/math] | [math]\displaystyle{ \tfrac{2G(1-\nu)}{1-2\nu} }[/math] | |||
| [math]\displaystyle{ (G,\,M) }[/math] | [math]\displaystyle{ M - \tfrac{4G}{3} }[/math] | [math]\displaystyle{ \tfrac{G(3M-4G)}{M-G} }[/math] | [math]\displaystyle{ M - 2G\, }[/math] | [math]\displaystyle{ \tfrac{M - 2G}{2M - 2G} }[/math] | |||
| [math]\displaystyle{ (\nu,\,M) }[/math] | [math]\displaystyle{ \tfrac{M(1+\nu)}{3(1-\nu)} }[/math] | [math]\displaystyle{ \tfrac{M(1+\nu)(1-2\nu)}{1-\nu} }[/math] | [math]\displaystyle{ \tfrac{M \nu}{1-\nu} }[/math] | [math]\displaystyle{ \tfrac{M(1-2\nu)}{2(1-\nu)} }[/math] | |||
 |