Physics:Fluorescence interference contrast microscopy

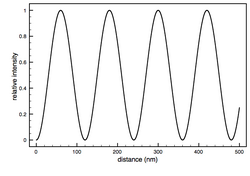
Fluorescence interference contrast (FLIC) microscopy is a microscopic technique developed to achieve z-resolution on the nanometer scale. FLIC occurs whenever fluorescent objects are in the vicinity of a reflecting surface (e.g. Si wafer). The resulting interference between the direct and the reflected light leads to a double sin² modulation of the intensity, I, of a fluorescent object as a function of distance, h, above the reflecting surface. This allows for the nanometer height measurements.

FLIC microscope is well suited to measuring the topography of a membrane that contains fluorescent probes e.g. an artificial lipid bilayer, or a living cell membrane or the structure of fluorescently labeled proteins on a surface.

FLIC optical theory

General two layer system

The optical theory underlying FLIC was developed by Armin Lambacher and Peter Fromherz. They derived a relationship between the observed fluorescence intensity and the distance of the fluorophore from a reflective silicon surface.

The observed fluorescence intensity, [math]\displaystyle{ I_{FLIC} }[/math], is the product of the excitation probability per unit time, [math]\displaystyle{ P_{ex} }[/math], and the probability of measuring an emitted photon per unit time, [math]\displaystyle{ P_{em} }[/math]. Both probabilities are a function of the fluorophore height above the silicon surface, so the observed intensity will also be a function of the fluorophore height. The simplest arrangement to consider is a fluorophore embedded in silicon dioxide (refractive index [math]\displaystyle{ n_{1} }[/math]) a distance d from an interface with silicon (refractive index [math]\displaystyle{ n_{0} }[/math]). The fluorophore is excited by light of wavelength [math]\displaystyle{ \lambda_{ex} }[/math] and emits light of wavelength [math]\displaystyle{ \lambda_{em} }[/math]. The unit vector [math]\displaystyle{ ''e_{ex}'' }[/math] gives the orientation of the transition dipole of excitation of the fluorophore. [math]\displaystyle{ P_{ex} }[/math] is proportional to the squared projection of the local electric field, [math]\displaystyle{ F_{in} }[/math], which includes the effects of interference, on the direction of the transition dipole.
[math]\displaystyle{ P_{ex}\propto \mid F_{in}\cdot e_{ex}\mid^{2} }[/math]
The local electric field, [math]\displaystyle{ F_{in} }[/math], at the fluorophore is affected by interference between the direct incident light and the light reflecting off the silicon surface. The interference is quantified by the phase difference [math]\displaystyle{ \Phi_{in} }[/math] given by
[math]\displaystyle{ \Phi_{in} = \frac{4\pi n_{1}d\cos \theta^{in}_{1}}{\lambda_{ex}} }[/math]
[math]\displaystyle{ \theta^{in}_{1} }[/math] is the angle of the incident light with respect to the silicon plane normal. Not only does interference modulate [math]\displaystyle{ F_{in} }[/math], but the silicon surface does not perfectly reflect the incident light. Fresnel coefficients give the change in amplitude between an incident and reflected wave. The Fresnel coefficients depend on the angles of incidence, [math]\displaystyle{ \theta_{i} }[/math] and [math]\displaystyle{ \theta_{j} }[/math], the indices of refraction of the two mediums and the polarization direction. The angles [math]\displaystyle{ \theta_{i} }[/math] and [math]\displaystyle{ \theta_{j} }[/math] can be related by Snell's Law. The expressions for the reflection coefficients are:
[math]\displaystyle{ r^{TE}_{ij} = \frac{n_{i}\cos \theta_{i} - n_{j}\cos \theta_{j}}{n_{i}\cos \theta_{i} + n_{j}\cos \theta_{j}}\quad r^{TM}_{ij} = \frac{n_{j}\cos \theta_{i} - n_{i}\cos \theta_{j}}{n_{j}\cos \theta_{i} + n_{i}\cos \theta_{j}} }[/math]
TE refers to the component of the electric field perpendicular to the plane of incidence and TM to the parallel component (The incident plane is defined by the plane normal and the propagation direction of the light). In cartesian coordinates, the local electric field is
[math]\displaystyle{ F_{in} = \sin \gamma_{in} \left[\begin{array}{c}0 \\1 + r^{TE}_{10}\textit{e}^{ i\Phi_{in}} \\0\end{array}\right] + \cos \gamma _{in} \left[\begin{array}{c}\cos \theta ^{in}_{1}(1-r^{TM}_{10}\textit{e}^{i\Phi_{in}}) \\0 \\ \sin \theta ^{in}_{1}(1+r^{TM}_{10}\textit{e}^{i\Phi_{in}})\end{array}\right] }[/math]
[math]\displaystyle{ \gamma_{in} }[/math] is the polarization angle of the incident light with respect to the plane of incidence. The orientation of the excitation dipole is a function of its angle [math]\displaystyle{ \theta_{ex} }[/math] to the normal and [math]\displaystyle{ \phi_{ex} }[/math] azimuthal to the plane of incidence.
[math]\displaystyle{ \textit{e}_{ex} = \left[\begin{array}{c}\cos \phi_{ex}\sin \theta_{ex}\\\sin \phi_{ex}\sin \theta_{ex} \\\cos \theta_{ex}\end{array}\right] }[/math]
The above two equations for [math]\displaystyle{ F_{in} }[/math] and [math]\displaystyle{ \textit{e}_{ex} }[/math] can be combined to give the probability of exciting the fluorophore per unit time [math]\displaystyle{ P_{ex} }[/math].
Many of the parameters used above would vary in a normal experiment. The variation in the five following parameters should be included in this theoretical description.

• The coherence of the excitation light
• The incident angle ([math]\displaystyle{ \theta^{in}_{1} }[/math]) of excitation light
• Polarization angle ([math]\displaystyle{ \gamma_{in} }[/math]) of the excitation light
• The angle of transition dipole ([math]\displaystyle{ \theta_{ex} }[/math]) of the fluorophore
• The wavelength of the excitation light ([math]\displaystyle{ \lambda_{ex} }[/math])

The squared projection [math]\displaystyle{ \mid F_{in}\cdot e_{ex}\mid^{2} }[/math] must be averaged over these quantities to give the probability of excitation [math]\displaystyle{ P_{ex} }[/math]. Averaging over the first 4 parameters gives
[math]\displaystyle{ \lt \mid F_{in}\cdot e_{ex}\mid^{2}\gt \propto \int \sin \theta_{1}^{in}d\theta_{1}^{in}A_{in}(\theta_{1}^{in}) \times \int \sin \theta_{ex}d\theta_{ex}O(\theta_{ex})U_{ex}(\lambda_{in},\theta_{1}^{in}.\theta_{ex}) }[/math] [math]\displaystyle{ U_{ex} = \sin^{2}\theta_{ex}\mid 1+r^{TE}_{10}\textit{e}^{i\Phi_{in}}\mid^{2} + \sin^{2}\theta_{ex}\cos^{2}\theta^{in}_{1}\mid 1-r^{TM}_{10}\textit{e}^{i\Phi_{in}}\mid^{2}+2\cos^{2}\theta_{ex}\sin^{2}\theta^{in}_{1}\mid 1+r^{TM}_{10}\textit{e}^{i\Phi_{in}}\mid^{2} }[/math]

Example of a FLIC intensity plot showing the relative fluorescence intensity measured versus the distance of the fluorophore from the reflective surface. The peaks might not be the same height in a real experimental plot

Normalization factors are not included. [math]\displaystyle{ O(\theta_{ex}) }[/math] is a distribution of the orientation angle of the fluorophore dipoles. The azimuthal angle [math]\displaystyle{ \phi_{ex} }[/math] and the polarization angle [math]\displaystyle{ \gamma_{in} }[/math] are integrated over analytically, so they no longer appear in the above equation. To finally obtain the probability of excitation per unit time, the above equation is integrated over the spread in excitation wavelength, accounting for the intensity [math]\displaystyle{ I(\lambda_{ex}) }[/math] and the extinction coefficient of the fluorophore [math]\displaystyle{ \epsilon(\lambda_{ex}) }[/math].
[math]\displaystyle{ P_{ex}\propto \int d\lambda_{ex}I(\lambda_{ex})\epsilon(\lambda_{ex})\lt \mid F_{in}\cdot e_{ex}\mid^{2}\gt }[/math]
The steps to calculate [math]\displaystyle{ P_{em} }[/math] are equivalent to those above in calculating [math]\displaystyle{ P_{ex} }[/math] except that the parameter labels em are replaced with ex and in is replaced with out.
[math]\displaystyle{ P_{em}\propto \int d\lambda_{em}\Phi_{det}(\lambda_{em})\textit{f}(\lambda_{em})\lt \mid F_{in}\cdot e_{ex}\mid^{2}\gt }[/math]
The resulting fluorescence intensity measured is proportional to the product of the excitation probability and emission probability

[math]\displaystyle{ I_{FLIC} \propto P_{ex}P_{em} }[/math]
It is important to note that this theory determines a proportionality relation between the measured fluorescence intensity [math]\displaystyle{ I_{FLIC} }[/math] and the distance of the fluorophore above the reflective surface. The fact that it is not an equality relation will have a significant effect on the experimental procedure.

Experimental Setup

A silicon wafer is typically used as the reflective surface in a FLIC experiment. An oxide layer is then thermally grown on top of the silicon wafer to act as a spacer. On top of the oxide is placed the fluorescently labeled specimen, such as a lipid membrane, a cell or membrane bound proteins. With the sample system built, all that is needed is an epifluorescence microscope and a CCD camera to make quantitative intensity measurements.

This is a diagram of an example FLIC experimental setup with silicon, three oxide layers and a fluorescently labeled lipid bilayer (the yellow stars represent fluorophores.

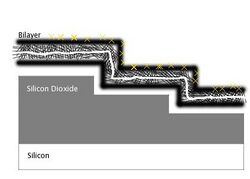
The silicon dioxide thickness is very important in making accurate FLIC measurements. As mentioned before, the theoretical model describes the relative fluorescence intensity measured versus the fluorophore height. The fluorophore position cannot be simply read off of a single measured FLIC curve. The basic procedure is to manufacture the oxide layer with at least two known thicknesses (the layer can be made with photolithographic techniques and the thickness measured by ellipsometry). The thicknesses used depends on the sample being measured. For a sample with fluorophore height in the range of 10 nm, oxide thickness around 50 nm would be best because the FLIC intensity curve is steepest here and would produce the greatest contrast between fluorophore heights. Oxide thickness above a few hundred nanometers could be problematic because the curve begins to get smeared out by polychromatic light and a range of incident angles. A ratio of measured fluorescence intensities at different oxide thicknesses is compared to the predicted ratio to calculate the fluorophore height above the oxide ([math]\displaystyle{ d_{\textit{f}}, }[/math]).
[math]\displaystyle{ \frac{I_{theory}(d_{1})}{I_{theory}(d_{0})}=\frac{I_{exp}(d_{1}+d_{\textit{f}})}{I_{exp}(d_{0}+d_{\textit{f}})} }[/math]
The above equation can then be solved numerically to find [math]\displaystyle{ d_{\textit{f}} }[/math]. Imperfections of the experiment, such as imperfect reflection, nonnormal incidence of light and polychromatic light tend to smear out the sharp fluorescence curves. The spread in incidence angle can be controlled by the numerical aperture (N.A.). However, depending on the numerical aperture used, the experiment will yield good lateral resolution (x-y) or good vertical resolution (z), but not both. A high N.A. (~1.0) gives good lateral resolution which is best if the goal is to determine long range topography. Low N.A. (~0.001), on the other hand, provides accurate z-height measurement to determine the height of a fluorescently labeled molecule in a system.

Analysis

Example of experimental data collected for a fluorescently labeled sample over 16 oxide thicknesses. Fitting the curve to the 16 data points would give the height of the fluorophores above the oxide surface.

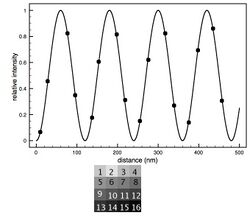
The basic analysis involves fitting the intensity data with the theoretical model allowing the distance of the fluorophore above the oxide surface ([math]\displaystyle{ d_{\textit{f}} }[/math]) to be a free parameter. The FLIC curves shift to the left as the distance of the fluorophore above the oxide increases. [math]\displaystyle{ d_{\textit{f}} }[/math] is usually the parameter of interest, but several other free parameters are often included to optimize the fit. Normally an amplitude factor (a) and a constant additive term for the background (b) are included. The amplitude factor scales the relative model intensity and the constant background shifts the curve up or down to account for fluorescence coming from out of focus areas, such as the top side of a cell. Occasionally the numerical aperture (N.A.) of the microscope is allowed to be a free parameter in the fitting. The other parameters entering the optical theory, such as different indices of refraction, layer thicknesses and light wavelengths, are assumed constant with some uncertainty. A FLIC chip may be made with oxide terraces of 9 or 16 different heights arranged in blocks. After a fluorescence image is captured, each 9 or 16 terrace block yields a separate FLIC curve that defines a unique [math]\displaystyle{ d_{\textit{f}} }[/math]. The average [math]\displaystyle{ d_{\textit{f}} }[/math] is found by compiling all the [math]\displaystyle{ d_{\textit{f}} }[/math] values into a histogram.
The statistical error in the calculation of [math]\displaystyle{ d_{\textit{f}} }[/math] comes from two sources: the error in fitting of the optical theory to the data and the uncertainty in the thickness of the oxide layer. Systematic error comes from three sources: the measurement of the oxide thickness (usually by ellipsometer), the fluorescence intensity measurement with the CCD, and the uncertainty in the parameters used in the optical theory. The systematic error has been estimated to be [math]\displaystyle{ \sim 1 nm }[/math].

References

• Ajo-Franklin, Caroline M.; Yoshina-Ishii, Chiaki; Boxer, Steven G. (2005). "Probing the Structure of Supported Membranes and Tethered Oligonucleotides by Fluorescence Interference Contrast Microscopy". Langmuir (American Chemical Society (ACS)) 21 (11): 4976–4983. doi:10.1021/la0468388. ISSN 0743-7463. PMID 15896039. 
• Braun, D.; Fromherz, P. (1997-10-01). "Fluorescence interference-contrast microscopy of cell adhesion on oxidized silicon". Applied Physics A: Materials Science & Processing (Springer Science and Business Media LLC) 65 (4–5): 341–348. doi:10.1007/s003390050589. ISSN 0947-8396. Bibcode: 1997ApPhA..65..341B. 
• Braun, Dieter; Fromherz, Peter (1998-12-07). "Fluorescence Interferometry of Neuronal Cell Adhesion on Microstructured Silicon". Physical Review Letters (American Physical Society (APS)) 81 (23): 5241–5244. doi:10.1103/physrevlett.81.5241. ISSN 0031-9007. Bibcode: 1998PhRvL..81.5241B. 
• Crane, Jonathan M.; Kiessling, Volker; Tamm, Lukas K. (2005). "Measuring Lipid Asymmetry in Planar Supported Bilayers by Fluorescence Interference Contrast Microscopy". Langmuir (American Chemical Society (ACS)) 21 (4): 1377–1388. doi:10.1021/la047654w. ISSN 0743-7463. PMID 15697284. 
• Kaizuka, Yoshihisa; Groves, Jay T. (2006-03-20). "Hydrodynamic Damping of Membrane Thermal Fluctuations near Surfaces Imaged by Fluorescence Interference Microscopy". Physical Review Letters (American Physical Society (APS)) 96 (11): 118101. doi:10.1103/physrevlett.96.118101. ISSN 0031-9007. PMID 16605875. Bibcode: 2006PhRvL..96k8101K. 
• Kiessling, Volker; Tamm, Lukas K. (2003). "Measuring Distances in Supported Bilayers by Fluorescence Interference-Contrast Microscopy: Polymer Supports and SNARE Proteins". Biophysical Journal (Elsevier BV) 84 (1): 408–418. doi:10.1016/s0006-3495(03)74861-9. ISSN 0006-3495. PMID 12524294. Bibcode: 2003BpJ....84..408K. 
• Lambacher, Armin; Fromherz, Peter (1996). "Fluorescence interference-contrast microscopy on oxidized silicon using a monomolecular dye layer". Applied Physics A: Materials Science & Processing (Springer Science and Business Media LLC) 63 (3): 207–216. doi:10.1007/bf01567871. ISSN 0947-8396. Bibcode: 1996ApPhA..63..207L. 
• Lambacher, Armin; Fromherz, Peter (2002-06-01). "Luminescence of dye molecules on oxidized silicon and fluorescence interference contrast microscopy of biomembranes". Journal of the Optical Society of America B (The Optical Society) 19 (6): 1435–1453. doi:10.1364/josab.19.001435. ISSN 0740-3224. Bibcode: 2002JOSAB..19.1435L. 
• Parthasarathy, Raghuveer; Groves, Jay T. (2004). "Optical Techniques for Imaging Membrane Topography". Cell Biochemistry and Biophysics (Springer Science and Business Media LLC) 41 (3): 391–414. doi:10.1385/cbb:41:3:391. ISSN 1085-9195. PMID 15509889.