Physics:Coherence
In physics, coherence expresses the potential for two waves to interfere. Two monochromatic beams from a single source always interfere.[1]: 256 Physical sources are not strictly monochromatic: they may be partly coherent. Beams from different sources are mutually incoherent.
When interfering, two waves add together to create a wave of greater amplitude than either one (constructive interference) or subtract from each other to create a wave of minima which may be zero[1]: 256 (destructive interference), depending on their relative phase. Constructive or destructive interference are limit cases, and two waves always interfere, even if the result of the addition is complicated or not remarkable.
Two waves with constant relative phase will be coherent.[2] The amount of coherence can readily be measured by the interference visibility, which looks at the size of the interference fringes relative to the input waves (as the phase offset is varied); a precise mathematical definition of the degree of coherence is given by means of correlation functions. More generally, coherence describes the statistical similarity of a field (electromagnetic field, quantum wave packet etc.) at two points in space or time.[3]
Qualitative concept

Coherence controls the visibility or contrast of interference patterns. For example, visibility of the double slit experiment pattern requires that both slits be illuminated by a coherent wave as illustrated in the figure. Large sources without collimation or sources that mix many different frequencies will have lower visibility.[4]: 264
Coherence contains several distinct concepts. Spatial coherence describes the correlation (or predictable relationship) between waves at different points in space, either lateral or longitudinal.[5] Temporal coherence describes the correlation between waves observed at different moments in time. Both are observed in the Michelson–Morley experiment and Young's interference experiment. Once the fringes are obtained in the Michelson interferometer, when one of the mirrors is moved away gradually from the beam-splitter, the time for the beam to travel increases and the fringes become dull and finally disappear, showing temporal coherence. Similarly, in a double-slit experiment, if the space between the two slits is increased, the coherence dies gradually and finally the fringes disappear, showing spatial coherence. In both cases, the fringe amplitude slowly disappears, as the path difference increases past the coherence length.
Coherence was originally conceived in connection with Thomas Young's double-slit experiment in optics but is now used in any field that involves waves, such as acoustics, electrical engineering, neuroscience, and quantum mechanics. The property of coherence is the basis for commercial applications such as holography, the Sagnac gyroscope, radio antenna arrays, optical coherence tomography and telescope interferometers (Astronomical optical interferometers and radio telescopes).
Mathematical definition
The coherence function between two signals and is defined as[6]
where is the cross-spectral density of the signal and and are the power spectral density functions of and , respectively. The cross-spectral density and the power spectral density are defined as the Fourier transforms of the cross-correlation and the autocorrelation signals, respectively. For instance, if the signals are functions of time, the cross-correlation is a measure of the similarity of the two signals as a function of the time lag relative to each other and the autocorrelation is a measure of the similarity of each signal with itself in different instants of time. In this case the coherence is a function of frequency. Analogously, if and are functions of space, the cross-correlation measures the similarity of two signals in different points in space and the autocorrelations the similarity of the signal relative to itself for a certain separation distance. In that case, coherence is a function of wavenumber (spatial frequency).
The coherence varies in the interval . If it means that the signals are perfectly correlated or linearly related and if they are totally uncorrelated. If a linear system is being measured, being the input and the output, the coherence function will be unitary all over the spectrum. However, if non-linearities are present in the system the coherence will vary in the limit given above.
Coherence and correlation
The coherence of two waves expresses how well correlated the waves are as quantified by the cross-correlation function.[7][1][8][9][10] Cross-correlation quantifies the ability to predict the phase of the second wave by knowing the phase of the first. As an example, consider two waves perfectly correlated for all times (by using a monochromatic light source). At any time, the phase difference between the two waves will be constant. If, when they are combined, they exhibit perfect constructive interference, perfect destructive interference, or something in-between but with constant phase difference, then it follows that they are perfectly coherent. As will be discussed below, the second wave need not be a separate entity. It could be the first wave at a different time or position. In this case, the measure of correlation is the autocorrelation function (sometimes called self-coherence). Degree of correlation involves correlation functions.[11]: 545-550
Examples of wave-like states
These states are unified by the fact that their behavior is described by a wave equation or some generalization thereof.
- Waves in a rope (up and down) or slinky (compression and expansion)
- Surface waves in a liquid
- Electromagnetic signals (fields) in transmission lines
- Sound
- Radio waves and microwaves
- Light waves (optics)
- Matter waves associated with, for examples, electrons and atoms
In system with macroscopic waves, one can measure the wave directly. Consequently, its correlation with another wave can simply be calculated. However, in optics one cannot measure the electric field directly as it oscillates much faster than any detector's time resolution.[12] Instead, one measures the intensity of the light. Most of the concepts involving coherence which will be introduced below were developed in the field of optics and then used in other fields. Therefore, many of the standard measurements of coherence are indirect measurements, even in fields where the wave can be measured directly.
Temporal coherence


Temporal coherence is the measure of the average correlation between the value of a wave and itself delayed by τ, at any pair of times. Temporal coherence tells us how monochromatic a source is. In other words, it characterizes how well a wave can interfere with itself at a different time. The delay over which the phase or amplitude wanders by a significant amount (and hence the correlation decreases by significant amount) is defined as the coherence time τc. At a delay of τ=0 the degree of coherence is perfect, whereas it drops significantly as the delay passes τ=τc. The coherence length Lc is defined as the distance the wave travels in time τc.[11]: 560, 571–573
The coherence time is not the time duration of the signal; the coherence length differs from the coherence area (see below).
The relationship between coherence time and bandwidth
The larger the bandwidth – range of frequencies Δf a wave contains – the faster the wave decorrelates (and hence the smaller τc is):[11]: 358–359, 560
Formally, this follows from the convolution theorem in mathematics, which relates the Fourier transform of the power spectrum (the intensity of each frequency) to its autocorrelation.[11]: 572
Narrow bandwidth lasers have long coherence lengths (up to hundreds of meters). For example, a stabilized and monomode helium–neon laser can easily produce light with coherence lengths of 300 m.[15] Not all lasers have a highly monochromaticity, however (e.g. for a mode-locked Ti-sapphire laser, Δλ ≈ 2 nm - 70 nm).
LEDs are characterized by Δλ ≈ 50 nm, and tungsten filament lights exhibit Δλ ≈ 600 nm, so these sources have shorter coherence times than the most monochromatic lasers.
Examples of temporal coherence
Examples of temporal coherence include:
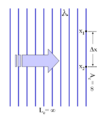
- A wave containing only a single frequency (monochromatic) is perfectly correlated with itself at all time delays, in accordance with the above relation. (See Figure 1)
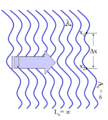
- Conversely, a wave whose phase drifts quickly will have a short coherence time. (See Figure 2)
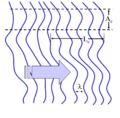
- Similarly, pulses (wave packets) of waves, which naturally have a broad range of frequencies, also have a short coherence time since the amplitude of the wave changes quickly. (See Figure 3)
- Finally, white light, which has a very broad range of frequencies, is a wave which varies quickly in both amplitude and phase. Since it consequently has a very short coherence time (just 10 periods or so), it is often called incoherent.
Holography requires light with a long coherence time. In contrast, optical coherence tomography, in its classical version, uses light with a short coherence time.
Measurement of temporal coherence


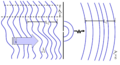
In optics, temporal coherence is measured in an interferometer such as the Michelson interferometer or Mach–Zehnder interferometer. In these devices, a wave is combined with a copy of itself that is delayed by time τ. A detector measures the time-averaged intensity of the light exiting the interferometer. The resulting visibility of the interference pattern (e.g. see Figure 4) gives the temporal coherence at delay τ. Since for most natural light sources, the coherence time is much shorter than the time resolution of any detector, the detector itself does the time averaging. Consider the example shown in Figure 3. At a fixed delay, here 2τc, an infinitely fast detector would measure an intensity that fluctuates significantly over a time t equal to τc. In this case, to find the temporal coherence at 2τc, one would manually time-average the intensity.
Spatial coherence
In some systems, such as water waves or optics, wave-like states can extend over one or two dimensions. Spatial coherence describes the ability for two spatial points x1 and x2 in the extent of a wave to interfere when averaged over time. More precisely, the spatial coherence is the cross-correlation between two points in a wave for all times. If a wave has only 1 value of amplitude over an infinite length, it is perfectly spatially coherent. The range of separation between the two points over which there is significant interference defines the diameter of the coherence area, Ac[16] (Coherence length, often a feature of a source, is usually an industrial term related to the coherence time of the source, not the coherence area in the medium.) Ac is the relevant type of coherence for the Young's double-slit interferometer. It is also used in optical imaging systems and particularly in various types of astronomy telescopes. Sometimes people also use "spatial coherence" to refer to the visibility when a wave-like state is combined with a spatially shifted copy of itself.
Examples
- Spatial coherence
-
Figure 5: A plane wave with an infinite coherence length.
-
Figure 6: A wave with a varying profile (wavefront) and infinite coherence length.
-
Figure 7: A wave with a varying profile (wavefront) and finite coherence length.
-
Figure 8: A wave with finite coherence area is incident on a pinhole (small aperture). The wave will diffract out of the pinhole. Far from the pinhole the emerging spherical wavefronts are approximately flat. The coherence area is now infinite while the coherence length is unchanged.
-
Figure 9: A wave with infinite coherence area is combined with a spatially shifted copy of itself. Some sections in the wave interfere constructively and some will interfere destructively. Averaging over these sections, a detector with length D will measure reduced interference visibility. For example, a misaligned Mach–Zehnder interferometer will do this.
Consider a tungsten light-bulb filament. Different points in the filament emit light independently and have no fixed phase-relationship. In detail, at any point in time the profile of the emitted light is going to be distorted. The profile will change randomly over the coherence time . Since for a white-light source such as a light-bulb is small, the filament is considered a spatially incoherent source. In contrast, a radio antenna array, has large spatial coherence because antennas at opposite ends of the array emit with a fixed phase-relationship. Light waves produced by a laser often have high temporal and spatial coherence (though the degree of coherence depends strongly on the exact properties of the laser). Spatial coherence of laser beams also manifests itself as speckle patterns and diffraction fringes seen at the edges of shadow.
Holography requires temporally and spatially coherent light. Its inventor, Dennis Gabor, produced successful holograms more than ten years before lasers were invented. To produce coherent light he passed the monochromatic light from an emission line of a mercury-vapor lamp through a pinhole spatial filter.
In February 2011 it was reported that helium atoms, cooled to near absolute zero / Bose–Einstein condensate state, can be made to flow and behave as a coherent beam as occurs in a laser.[17][18] Moreover, the coherence properties of the output light from multimode nonlinear optical structures were found to obey the optical thermodynamic theory.[19]
Spectral coherence of short pulses


Waves of different frequencies (in light these are different colours) can interfere to form a pulse if they have a fixed relative phase-relationship (see Fourier transform). Conversely, if waves of different frequencies are not coherent, then, when combined, they create a wave that is continuous in time (e.g. white light or white noise). The temporal duration of the pulse is limited by the spectral bandwidth of the light according to:
- ,
which follows from the properties of the Fourier transform and results in Küpfmüller's uncertainty principle (for quantum particles it also results in the Heisenberg uncertainty principle).
If the phase depends linearly on the frequency (i.e. ) then the pulse will have the minimum time duration for its bandwidth (a transform-limited pulse), otherwise it is chirped (see dispersion).
Measurement of spectral coherence
Measurement of the spectral coherence of light requires a nonlinear optical interferometer, such as an intensity optical correlator, frequency-resolved optical gating (FROG), or spectral phase interferometry for direct electric-field reconstruction (SPIDER).
Polarization and coherence
Light also has a polarization, which is the direction in which the electric or magnetic field oscillates. Unpolarized light is composed of incoherent light waves with random polarization angles. The electric field of the unpolarized light wanders in every direction and changes in phase over the coherence time of the two light waves. An absorbing polarizer rotated to any angle will always transmit half the incident intensity when averaged over time.
If the electric field wanders by a smaller amount the light will be partially polarized so that at some angle, the polarizer will transmit more than half the intensity. If a wave is combined with an orthogonally polarized copy of itself delayed by less than the coherence time, partially polarized light is created.
The polarization of a light beam is represented by a vector in the Poincaré sphere. For polarized light the end of the vector lies on the surface of the sphere, whereas the vector has zero length for unpolarized light. The vector for partially polarized light lies within the sphere.
Quantum coherence
The signature property of quantum matter waves, wave interference, relies on coherence. While initially patterned after optical coherence, the theory and experimental understanding of quantum coherence greatly expanded the topic.[20]
Matter wave coherence
The simplest extension of optical coherence applies optical concepts to matter waves. For example, when performing the double-slit experiment with atoms in place of light waves, a sufficiently collimated atomic beam creates a coherent atomic wave-function illuminating both slits.[21] Each slit acts as a separate but in-phase beam contributing to the intensity pattern on a screen. These two contributions give rise to an intensity pattern of bright bands due to constructive interference, interlaced with dark bands due to destructive interference, on a downstream screen. Many variations of this experiment have been demonstrated.[22]: 1057
As with light, transverse coherence (across the direction of propagation) of matter waves is controlled by collimation. Because light, at all frequencies, travels the same velocity, longitudinal and temporal coherence are linked; in matter waves these are independent. In matter waves, velocity (energy) selection controls longitudinal coherence and pulsing or chopping controls temporal coherence.[21]: 154
Quantum optics
The discovery of the Hanbury Brown and Twiss effect – correlation of light upon coincidence – triggered Glauber's creation[23] of uniquely quantum coherence analysis. Classical optical coherence becomes a classical limit for first-order quantum coherence; higher degree of coherence leads to many phenomena in quantum optics.
Macroscopic quantum coherence
Macroscopic scale quantum coherence leads to novel phenomena, the so-called macroscopic quantum phenomena. For instance, the laser, superconductivity and superfluidity are examples of highly coherent quantum systems whose effects are evident at the macroscopic scale. The macroscopic quantum coherence (off-diagonal long-range order, ODLRO)[24][25] for superfluidity, and laser light, is related to first-order (1-body) coherence/ODLRO, while superconductivity is related to second-order coherence/ODLRO. (For fermions, such as electrons, only even orders of coherence/ODLRO are possible.) For bosons, a Bose–Einstein condensate is an example of a system exhibiting macroscopic quantum coherence through a multiple occupied single-particle state.
The classical electromagnetic field exhibits macroscopic quantum coherence. The most obvious example is the carrier signal for radio and TV. They satisfy Glauber's quantum description of coherence.
Quantum coherence as a resource
Recently M. B. Plenio and co-workers constructed an operational formulation of quantum coherence as a resource theory. They introduced coherence monotones analogous to the entanglement monotones.[26] Quantum coherence has been shown to be equivalent to quantum entanglement[27] in the sense that coherence can be faithfully described as entanglement, and conversely that each entanglement measure corresponds to a coherence measure.
Applications
Holography
Coherent superpositions of optical wave fields include holography. Holographic photographs have been used as art and as difficult to forge security labels.
Non-optical wave fields
Further applications concern the coherent superposition of non-optical wave fields. In quantum mechanics for example one considers a probability field, which is related to the wave function (interpretation: density of the probability amplitude). Here the applications concern, among others, the future technologies of quantum computing and the already available technology of quantum cryptography. Additionally the problems of the following subchapter are treated.
Modal analysis
Coherence is used to check the quality of the transfer functions (FRFs) being measured. Low coherence can be caused by poor signal to noise ratio, and/or inadequate frequency resolution.
See also
- Physics:Atomic coherence – Type of state of an atom-electromagnetic field system
- Coherence length – Distance over which a propagating wave maintains a certain degree of coherence
- Physics:Coherent states
- Physics:Laser linewidth – The spectral linewidth of a laser beam
- Physics:Measurement in quantum mechanics – Interaction of a quantum system with a classical observer
- Physics:Measurement problem – Theoretical problem in quantum physics
- Physics:Monochromatic radiation – Electromagnetic radiation with a single constant frequency
- Optical heterodyne detection – Information method in electromagnetic radiation
- Biology:Quantum biology – Application of quantum mechanics and chemistry to biology
- Physics:Quantum Zeno effect – Quantum measurement phenomenon
References
- ↑ 1.0 1.1 1.2 M.Born; E. Wolf (1999). Principles of Optics (7th ed.). Cambridge University Press. ISBN 978-0-521-64222-4.
- ↑ Rudiger, Paschotta. "Article on Coherence in the RP Photonics Encyclopedia". https://www.rp-photonics.com/encyclopedia.html.
- ↑ Wolf, Emil (2007). Introduction to the theory of coherence and polarization of light. Cambridge: Cambridge University Press. ISBN 9780521822114. OCLC 149011826.
- ↑ Born, Max; Wolf, Emil (1993). Principles of optics: electromagnetic theory of propagation, interference and diffraction of light (6. ed., reprinted (with corrections) ed.). Oxford: Pergamon Press. ISBN 978-0-08-026481-3.
- ↑ Hecht (1998). Optics (3rd ed.). Addison Wesley Longman. pp. 554–574. ISBN 978-0-201-83887-9.
- ↑ Shin. K, Hammond. J. Fundamentals of signal processing for sound and vibration engineers. John Wiley & Sons, 2008.
- ↑ Rolf G. Winter; Aephraim M. Steinberg (2008). "Coherence". AccessScience (McGraw-Hill). doi:10.1036/1097-8542.146900. http://accessscience.com/content/Coherence/146900.
- ↑ Loudon, Rodney (2000). The Quantum Theory of Light. Oxford University Press. ISBN 978-0-19-850177-0.
- ↑ Leonard Mandel; Emil Wolf (1995). Optical Coherence and Quantum Optics. Cambridge University Press. ISBN 978-0-521-41711-2.
- ↑ Arvind Marathay (1982). Elements of Optical Coherence Theory. John Wiley & Sons. ISBN 978-0-471-56789-9.
- ↑ 11.0 11.1 11.2 11.3 Hecht, Eugene (2002) (in en). Optics (4th ed.). United States of America: Addison Wesley. ISBN 978-0-8053-8566-3.
- ↑ Peng, J.-L.; Liu, T.-A.; Shu, R.-H. (2008). "Optical frequency counter based on two mode-locked fiber laser combs". Applied Physics B 92 (4): 513. doi:10.1007/s00340-008-3111-6. Bibcode: 2008ApPhB..92..513P.
- ↑ Christopher Gerry; Peter Knight (2005). Introductory Quantum Optics. Cambridge University Press. ISBN 978-0-521-52735-4.
- ↑ This figure needs to be changed because, in this figure, the green wave is actually not a copy of the red wave; both are monochromatic waves with slightly different frequencies. A proper figure would be a combination of a chirp wave and its delayed copy to match the figure and the current figure description.
- ↑ Saleh, Teich. Fundamentals of Photonics. Wiley.
- ↑ Goodman (1985). Statistical Optics (1st ed.). Wiley-Interscience. pp. 210, 221. ISBN 978-0-471-01502-4.
- ↑ Hodgman, S. S.; Dall, R. G.; Manning, A. G.; Baldwin, K. G. H.; Truscott, A. G. (2011). "Direct Measurement of Long-Range Third-Order Coherence in Bose-Einstein Condensates". Science 331 (6020): 1046–1049. doi:10.1126/science.1198481. PMID 21350171. Bibcode: 2011Sci...331.1046H.
- ↑ Pincock, S. (25 February 2011). "Cool laser makes atoms march in time". ABC Science. ABC News Online. http://www.abc.net.au/science/articles/2011/02/25/3149175.htm.
- ↑ Selim, Mahmoud A.; Wu, Fan O.; Pyrialakos, Georgios G.; Khajavikhan, Mercedeh; Christodoulides, Demetrios (2023-03-01). "Coherence properties of light in highly multimoded nonlinear parabolic fibers under optical equilibrium conditions" (in EN). Optics Letters 48 (5): 1208–1211. doi:10.1364/OL.483282. ISSN 1539-4794. PMID 36857250. https://opg.optica.org/ol/abstract.cfm?uri=ol-48-5-1208.
- ↑ Streltsov, Alexander; Adesso, Gerardo; Plenio, Martin B. (2017-10-30). "Colloquium : Quantum coherence as a resource" (in en). Reviews of Modern Physics 89 (4): 041003. doi:10.1103/RevModPhys.89.041003. ISSN 0034-6861. https://link.aps.org/doi/10.1103/RevModPhys.89.041003.
- ↑ 21.0 21.1 Adams, C.S; Sigel, M; Mlynek, J (May 1994). "Atom optics" (in en). Physics Reports 240 (3): 143–210. doi:10.1016/0370-1573(94)90066-3.
- ↑ Cronin, Alexander D.; Schmiedmayer, Jörg; Pritchard, David E. (2009-07-28). "Optics and interferometry with atoms and molecules" (in en). Reviews of Modern Physics 81 (3): 1051–1129. doi:10.1103/RevModPhys.81.1051. ISSN 0034-6861. https://link.aps.org/doi/10.1103/RevModPhys.81.1051.
- ↑ Glauber, Roy J. (1963-06-15). "The Quantum Theory of Optical Coherence" (in en). Physical Review 130 (6): 2529–2539. doi:10.1103/PhysRev.130.2529. ISSN 0031-899X.
- ↑ Penrose, O.; Onsager, L. (1956). "Bose-Einstein Condensation and Liquid Helium". Phys. Rev. 104 (3): 576–584. doi:10.1103/physrev.104.576. Bibcode: 1956PhRv..104..576P.
- ↑ Yang, C.N. (1962). "Concept of Off-Diagonal Long-Range Order and the Quantum Phases of Liquid He and of Superconductors". Rev. Mod. Phys. 34 (4): 694–704. doi:10.1103/revmodphys.34.694. Bibcode: 1962RvMP...34..694Y.
- ↑ Baumgratz, T.; Cramer, M.; Plenio, M.B. (2014). "Quantifying Coherence". Phys. Rev. Lett. 113 (14): 140401. doi:10.1103/physrevlett.113.140401. PMID 25325620. Bibcode: 2014PhRvL.113n0401B.
- ↑ Tan, K.C.; Jeong, H. (2018). "Entanglement as the Symmetric Portion of Correlated Coherence". Phys. Rev. Lett. 121 (22): 220401. doi:10.1103/PhysRevLett.121.220401. PMID 30547638. Bibcode: 2018PhRvL.121v0401T.
External links
- Dr. SkySkull (2008-09-03). "Optics basics: Coherence". Skulls in the Stars. http://skullsinthestars.com/2008/09/03/optics-basics-coherence/.