Physics:Galileo's Leaning Tower of Pisa experiment

From HandWiki
Short description: Celebrated demonstration of gravity
Comparison of the antiquated view and the outcome of the experiment (size of the spheres represent their masses, not their volumes)

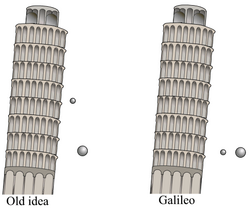
Between 1589 and 1592,[1] the Italian scientist Galileo Galilei (then professor of mathematics at the University of Pisa) is said to have dropped two spheres of the same volume but different masses from the Leaning Tower of Pisa to demonstrate that their time of descent was independent of their mass, according to a biography by Galileo's pupil Vincenzo Viviani, composed in 1654 and published in 1717.[2][3]:19–21[4][5] The basic premise had already been demonstrated by Italian experimenters a few decades earlier.

According to the story, Galileo discovered through this experiment that the objects fell with the same acceleration, proving his prediction true, while at the same time disproving Aristotle's theory of gravity (which states that objects fall at speed proportional to their mass). Most historians consider it to have been a thought experiment rather than a physical test.[6]

Background

Further information: Physics:History of gravitational theory

The 6th-century Byzantine Greek philosopher and Aristotelian commentator John Philoponus argued that the Aristotelian assertion that objects fall proportionately to their weight was incorrect.[7] By 1544, according to Benedetto Varchi, the Aristotelian premise was disproven experimentally by at least two Italians.[8] In 1551, Domingo de Soto suggested that objects in free fall accelerate uniformly.[8] Two years later, mathematician Giambattista Benedetti questioned why two balls, one made of iron and one of wood, would fall at the same speed.[8] All of this preceded the 1564 birth of Galileo Galilei.

Delft tower experiment

thumb|right|The Nieuwe Kerk in Delft, where the experiment by Stevin and de Groot took place

Main page: Delft tower experiment

A similar experiment was conducted in Delft in the Netherlands, by the mathematician and physicist Simon Stevin and Jan Cornets de Groot (the father of Hugo de Groot). The experiment is described in Stevin's 1586 book De Beghinselen der Weeghconst (The Principles of Statics), a landmark book on statics:

Let us take (as the highly educated Jan Cornets de Groot, the diligent researcher of the mysteries of Nature, and I have done) two balls of lead, the one ten times bigger and heavier than the other, and let them drop together from 30 feet high, and it will show, that the lightest ball is not ten times longer under way than the heaviest, but they fall together at the same time on the ground. ... This proves that Aristotle is wrong.[9][10][11]

Galileo's experiment

At the time when Viviani asserts that the experiment took place, Galileo had not yet formulated the final version of his law of falling bodies. He had, however, formulated an earlier version which predicted that bodies of the same material falling through the same medium would fall at the same speed.[3]:20 This was contrary to what Aristotle had taught: that heavy objects fall faster than the lighter ones, and in direct proportion to their weight.[3]:9[12] While this story has been retold in popular accounts, there is no account by Galileo himself of such an experiment, and many historians believe that it was a thought experiment.[13] An exception is Stillman Drake, who argues that it took place, more or less as Viviani described it, as a demonstration for students.[3]:19–21, 414–416

Galileo's thought experiment concerned the outcome (c) of attaching a small stone (a) to a larger one (b)

Galileo set out his ideas about falling people, and about projectiles in general, in his book Two New Sciences (1638). The two sciences were the science of motion, which became the foundation-stone of physics, and the science of materials and construction, an important contribution to engineering. Galileo arrived at his hypothesis by a famous thought experiment outlined in his book On Motion.[14] He writes:

Salviati. If then we take two bodies whose natural speeds are different, it is clear that on uniting the two, the more rapid one will be partly retarded by the slower, and the slower will be somewhat hastened by the swifter. Do you not agree with me in this opinion?

Simplicio. You are unquestionably right.

Salviati. But if this is true, and if a large stone moves with a speed of, say, eight while a smaller moves with a speed of four, then when they are united, the system will move with a speed less than eight; but the two stones when tied together make a stone larger than that which before moved with a speed of eight. Hence the heavier body moves with less speed than the lighter; an effect which is contrary to your supposition. Thus you see how, from your assumption that the heavier body moves more rapidly than the lighter one, I infer that the heavier body moves more slowly.[15]

His argument is that if we assume heavier objects do indeed fall faster than lighter ones (and conversely, lighter objects fall slower), the string will soon pull taut as the lighter object retards the fall of the heavier object. But the system considered as a whole is heavier than the heavy object alone, and therefore should fall faster. This contradiction leads one to conclude the assumption is false.

Later performances

right|thumb|Hammer and feather drop on the Moon by astronaut [[David Scott, Apollo 15 (1.38 MB, ogg/Theora format)]]

Astronaut David Scott performed a version of the experiment on the Moon during the Apollo 15 mission in 1971, dropping a feather and a hammer from his hands. Because of the negligible lunar atmosphere, there was no drag on the feather, which reached the lunar surface at the same time as the hammer.[16]

The basic premise behind these experiments is now known as the (weak) equivalence principle. Galileo's hypothesis that inertial mass (resistance to acceleration) equals gravitational mass (weight) was extended by Albert Einstein to include special relativity and that combination became a key concept leading to the development of the modern theory of gravity, general relativity. Physical experiments following Galileo increased the precision of the equivalence to better than one part in a trillion.[17]

See also

  • Delft tower experiment
  • Terminal velocity (An object dropped through air from a sufficient height will reach a steady speed, called the terminal velocity, when the aerodynamic drag force pushing up on the body balances the gravitational force (weight) pulling the body down.)
  • Nordtvedt effect
  • Newton's second law
  • Law of Inertia

Notes

  1. ↑ Some contemporary sources speculate about the exact date; e.g. Rachel Hilliam gives 1591 (Galileo Galilei: Father of Modern Science, The Rosen Publishing Group, 2005, p. 101).
  2. ↑ Vincenzo Viviani (1717), Racconto istorico della vita di Galileo Galilei, p. 606: [...dimostrando ciò con replicate esperienze, fatte dall'altezza del Campanile di Pisa con l'intervento delli altri lettori e filosofi e di tutta la scolaresca... [...Galileo showed this [all bodies, whatever their weights, fall with equal speeds] by repeated experiments made from the height of the Leaning Tower of Pisa in the presence of other professors and all the students...].
  3. ↑ 3.0 3.1 3.2 3.3 Drake, Stillman (2003). Galileo at Work: His Scientific Biography (Facsim. ed.). Mineola (N.Y.): Dover publ.. ISBN 9780486495422. 
  4. ↑ "Sci Tech : Science history: setting the record straight". The Hindu. June 30, 2005. http://www.hindu.com/seta/2005/06/30/stories/2005063000351500.htm. 
  5. ↑ Vincenzo Viviani on museo galileo
  6. ↑ "El experimento más famoso de Galileo probablemente nunca tuvo lugar". May 16, 2019. https://theconversation.com/el-experimento-mas-famoso-de-galileo-probablemente-nunca-tuvo-lugar-111650. 
  7. ↑ Wildberg, Christian, "John Philoponus", The Stanford Encyclopedia of Philosophy (Winter 2018 Edition), Edward N. Zalta (ed.) "As regards the natural motion of bodies falling through a medium, it was Aristotle's contention that the speed is proportional to the weight of the moving bodies and indirectly proportional to the density of the medium. Philoponus repudiates this view by appeal to the same kind of experiment that Galileo was to carry out centuries later (In Phys. 682–84)."
  8. ↑ 8.0 8.1 8.2 Wallace, William A. (2018) (in en). Domingo de Soto and the Early Galileo: Essays on Intellectual History. Abingdon, UK: Routledge. pp. 119, 121–22. ISBN 978-1-351-15959-3. https://books.google.com/books?id=8GxQDwAAQBAJ&pg=PR21. 
  9. ↑ Laet nemen (soo den hoochgheleerden H. IAN CORNETS DE GROOT vlietichste ondersoucker der Naturens verborghentheden, ende ick ghedaen hebben) twee loyen clooten d'een thienmael grooter en swaerder als d'ander, die laet t'samen vallen van 30 voeten hooch, op een bart oft yet daer sy merckelick gheluyt tegen gheven, ende sal blijcken, dat de lichste gheen thienmael langher op wech en blijft dan de swaerste, maer datse t'samen so ghelijck opt bart vallen, dat haer beyde gheluyden een selve clop schijnt te wesen. S'ghelijcx bevint hem daetlick oock also, met twee evegroote lichamen in thienvoudighe reden der swaerheyt, daerom Aristoteles voornomde everedenheyt is onrecht. In: Simon Stevin, De Beghinselen der Weeghconst, 1586.
  10. ↑ Asimov, Isaac (1964). Asimov's Biographical Encyclopedia of Science and Technology. ISBN:978-0385177719
  11. ↑ E. J. Dijksterhuis, ed., The Principal Works of Simon Stevin. Amsterdam, Netherlands: C. V. Swets & Zeitlinger, 1955 vol. 1, pp. 509, 511.
  12. ↑ Sharratt, M. (1994). Galileo: Decisive Innovator. Cambridge University Press. p. 31. ISBN 0-521-56671-1. 
  13. ↑ Groleau, R. (July 2002). "Galileo's Battle for the Heavens". https://www.pbs.org/wgbh/nova/galileo/experiments.html. 
  14. ↑ Van Helden, Albert (1995). "On Motion". The Galileo Project. http://galileo.rice.edu/sci/theories/on_motion.html. 
  15. ↑ "Galileo on Aristotle and Acceleration". http://galileoandeinstein.physics.virginia.edu/tns61.htm. 
  16. ↑ "The Apollo 15 Hammer-Feather Drop". https://moon.nasa.gov/resources/331/the-apollo-15-hammer-feather-drop/. 
  17. ↑ Schlamminger, Stephan; Choi, Ki-Young; Wagner, Todd A.; Gundlach, Jens H.; Adelberger, Eric G. (2008). "Test of the Equivalence Principle Using a Rotating Torsion Balance". Physical Review Letters 100 (4): 041101. doi:10.1103/PhysRevLett.100.041101. PMID 18352252. Bibcode: 2008PhRvL.100d1101S. 

Further reading

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Galileo%27s_Leaning_Tower_of_Pisa_experiment&oldid=3284775"