Physics:General relativity
| General relativity |
|---|
 |
File:BBH gravitational lensing of gw150914.webm General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalises special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time or four-dimensional spacetime. In particular, the curvature of spacetime is directly related to the energy and momentum of whatever matter and radiation are present. The relation is specified by the Einstein field equations, a system of second order partial differential equations.
Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gravitation in classical physics. These predictions concern the passage of time, the geometry of space, the motion of bodies in free fall, and the propagation of light, and include gravitational time dilation, gravitational lensing, the gravitational redshift of light, the Shapiro time delay and singularities/black holes. So far, all tests of general relativity have been shown to be in agreement with the theory. The time-dependent solutions of general relativity enable us to talk about the history of the universe and have provided the modern framework for cosmology, thus leading to the discovery of the Big Bang and cosmic microwave background radiation. Despite the introduction of a number of alternative theories, general relativity continues to be the simplest theory consistent with experimental data.
Reconciliation of general relativity with the laws of quantum physics remains a problem, however, as there is a lack of a self-consistent theory of quantum gravity. It is not yet known how gravity can be unified with the three non-gravitational forces: strong, weak and electromagnetic.
Einstein's theory has astrophysical implications, including the prediction of black holes—regions of space in which space and time are distorted in such a way that nothing, not even light, can escape from them. Black holes are the end-state for massive stars. Microquasars and active galactic nuclei are believed to be stellar black holes and supermassive black holes. It also predicts gravitational lensing, where the bending of light results in multiple images of the same distant astronomical phenomenon. Other predictions include the existence of gravitational waves, which have been observed directly by the physics collaboration LIGO and other observatories. In addition, general relativity has provided the base of cosmological models of an expanding universe.
Widely acknowledged as a theory of extraordinary beauty, general relativity has often been described as the most beautiful of all existing physical theories.[2]
History
Henri Poincaré's 1905 theory of the dynamics of the electron was a relativistic theory which he applied to all forces, including gravity. While others thought that gravity was instantaneous or of electromagnetic origin, he suggested that relativity was "something due to our methods of measurement". In his theory, he showed that gravitational waves propagate at the speed of light.[3] Soon afterwards, Einstein started thinking about how to incorporate gravity into his relativistic framework. In 1907, beginning with a simple thought experiment involving an observer in free fall (FFO), he embarked on what would be an eight-year search for a relativistic theory of gravity. After numerous detours and false starts, his work culminated in the presentation to the Prussian Academy of Science in November 1915 of what are now known as the Einstein field equations, which form the core of Einstein's general theory of relativity.[4] These equations specify how the geometry of space and time is influenced by whatever matter and radiation are present.[5] A version of non-Euclidean geometry, called Riemannian geometry, enabled Einstein to develop general relativity by providing the key mathematical framework on which he fit his physical ideas of gravity.[6] This idea was pointed out by mathematician Marcel Grossmann and published by Grossmann and Einstein in 1913.[7]
The Einstein field equations are nonlinear and considered difficult to solve. Einstein used approximation methods in working out initial predictions of the theory. But in 1916, the astrophysicist Karl Schwarzschild found the first non-trivial exact solution to the Einstein field equations, the Schwarzschild metric. This solution laid the groundwork for the description of the final stages of gravitational collapse, and the objects known today as black holes. In the same year, the first steps towards generalizing Schwarzschild's solution to electrically charged objects were taken, eventually resulting in the Reissner–Nordström solution, which is now associated with electrically charged black holes.[8] In 1917, Einstein applied his theory to the universe as a whole, initiating the field of relativistic cosmology. In line with contemporary thinking, he assumed a static universe, adding a new parameter to his original field equations—the cosmological constant—to match that observational presumption.[9] By 1929, however, the work of Hubble and others had shown that our universe is expanding. This is readily described by the expanding cosmological solutions found by Friedmann in 1922, which do not require a cosmological constant. Lemaître used these solutions to formulate the earliest version of the Big Bang models, in which our universe has evolved from an extremely hot and dense earlier state.[10] Einstein later declared the cosmological constant the biggest blunder of his life.[11]
During that period, general relativity remained something of a curiosity among physical theories. It was clearly superior to Newtonian gravity, being consistent with special relativity and accounting for several effects unexplained by the Newtonian theory. Einstein showed in 1915 how his theory explained the anomalous perihelion advance of the planet Mercury without any arbitrary parameters ("fudge factors"),[12] and in 1919 an expedition led by Eddington confirmed general relativity's prediction for the deflection of starlight by the Sun during the total solar eclipse of 29 May 1919,[13] instantly making Einstein famous.[14] Yet the theory remained outside the mainstream of theoretical physics and astrophysics until developments between approximately 1960 and 1975, now known as the golden age of general relativity.[15] Physicists began to understand the concept of a black hole, and to identify quasars as one of these objects' astrophysical manifestations.[16] Ever more precise solar system tests confirmed the theory's predictive power,[17] and relativistic cosmology also became amenable to direct observational tests.[18]
General relativity has acquired a reputation as a theory of extraordinary beauty.[2][19][20] Subrahmanyan Chandrasekhar has noted that at multiple levels, general relativity exhibits what Francis Bacon has termed a "strangeness in the proportion" (i.e. elements that excite wonderment and surprise). It juxtaposes fundamental concepts (space and time versus matter and motion) which had previously been considered as entirely independent. Chandrasekhar also noted that Einstein's only guides in his search for an exact theory were the principle of equivalence and his sense that a proper description of gravity should be geometrical at its basis, so that there was an "element of revelation" in the manner in which Einstein arrived at his theory.[21] Other elements of beauty associated with the general theory of relativity are its simplicity and symmetry, the manner in which it incorporates invariance and unification, and its perfect logical consistency.[22]
In the preface to Relativity: The Special and the General Theory, Einstein said "The present book is intended, as far as possible, to give an exact insight into the theory of Relativity to those readers who, from a general scientific and philosophical point of view, are interested in the theory, but who are not conversant with the mathematical apparatus of theoretical physics. The work presumes a standard of education corresponding to that of a university matriculation examination, and, despite the shortness of the book, a fair amount of patience and force of will on the part of the reader. The author has spared himself no pains in his endeavour to present the main ideas in the simplest and most intelligible form, and on the whole, in the sequence and connection in which they actually originated."[23]
From classical mechanics to general relativity
General relativity can be understood by examining its similarities with and departures from classical physics. The first step is the realization that classical mechanics and Newton's law of gravity admit a geometric description. The combination of this description with the laws of special relativity results in a heuristic derivation of general relativity.[24][25]
Geometry of Newtonian gravity

At the base of classical mechanics is the notion that a body's motion can be described as a combination of free (or inertial) motion, and deviations from this free motion. Such deviations are caused by external forces acting on a body in accordance with Newton's second law of motion, which states that the net force acting on a body is equal to that body's (inertial) mass multiplied by its acceleration.[26] The preferred inertial motions are related to the geometry of space and time: in the standard reference frames of classical mechanics, objects in free motion move along straight lines at constant speed. In modern parlance, their paths are geodesics, straight world lines in curved spacetime.[27]
Conversely, one might expect that inertial motions, once identified by observing the actual motions of bodies and making allowances for the external forces (such as electromagnetism or friction), can be used to define the geometry of space, as well as a time coordinate. However, there is an ambiguity once gravity comes into play. According to Newton's law of gravity, and independently verified by experiments such as that of Eötvös and its successors (see Eötvös experiment), there is a universality of free fall (also known as the weak equivalence principle, or the universal equality of inertial and passive-gravitational mass): the trajectory of a test body in free fall depends only on its position and initial speed, but not on any of its material properties.[28] A simplified version of this is embodied in Einstein's elevator experiment, illustrated in the figure on the right: for an observer in an enclosed room, it is impossible to decide, by mapping the trajectory of bodies such as a dropped ball, whether the room is stationary in a gravitational field and the ball accelerating, or in free space aboard a rocket that is accelerating at a rate equal to that of the gravitational field versus the ball which upon release has nil acceleration.[29]
Given the universality of free fall, there is no observable distinction between inertial motion and motion under the influence of the gravitational force. This suggests the definition of a new class of inertial motion, namely that of objects in free fall under the influence of gravity. This new class of preferred motions, too, defines a geometry of space and time—in mathematical terms, it is the geodesic motion associated with a specific connection which depends on the gradient of the gravitational potential. Space, in this construction, still has the ordinary Euclidean geometry. However, spacetime as a whole is more complicated. As can be shown using simple thought experiments following the free-fall trajectories of different test particles, the result of transporting spacetime vectors that can denote a particle's velocity (time-like vectors) will vary with the particle's trajectory; mathematically speaking, the Newtonian connection is not integrable. From this, one can deduce that spacetime is curved. The resulting Newton–Cartan theory is a geometric formulation of Newtonian gravity using only covariant concepts, i.e. a description which is valid in any desired coordinate system.[30] In this geometric description, tidal effects—the relative acceleration of bodies in free fall—are related to the derivative of the connection, showing how the modified geometry is caused by the presence of mass.[31]
Relativistic generalization
As intriguing as geometric Newtonian gravity may be, its basis, classical mechanics, is merely a limiting case of (special) relativistic mechanics.[32] In the language of symmetry: where gravity can be neglected, physics is Lorentz invariant as in special relativity rather than Galilei invariant as in classical mechanics. (The defining symmetry of special relativity is the Poincaré group, which includes translations, rotations, boosts and reflections.) The differences between the two become significant when dealing with speeds approaching the speed of light, and with high-energy phenomena.[33]
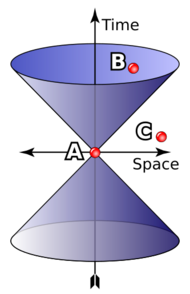
With Lorentz symmetry, additional structures come into play. They are defined by the set of light cones (see image). The light-cones define a causal structure: for each event A, there is a set of events that can, in principle, either influence or be influenced by A via signals or interactions that do not need to travel faster than light (such as event B in the image), and a set of events for which such an influence is impossible (such as event C in the image). These sets are observer-independent.[34] In conjunction with the world-lines of freely falling particles, the light-cones can be used to reconstruct the spacetime's semi-Riemannian metric, at least up to a positive scalar factor. In mathematical terms, this defines a conformal structure[35] or conformal geometry.
Special relativity is defined in the absence of gravity. For practical applications, it is a suitable model whenever gravity can be neglected. Bringing gravity into play, and assuming the universality of free fall motion, an analogous reasoning as in the previous section applies: there are no global inertial frames. Instead there are approximate inertial frames moving alongside freely falling particles. Translated into the language of spacetime: the straight time-like lines that define a gravity-free inertial frame are deformed to lines that are curved relative to each other, suggesting that the inclusion of gravity necessitates a change in spacetime geometry.[36]
A priori, it is not clear whether the new local frames in free fall coincide with the reference frames in which the laws of special relativity hold—that theory is based on the propagation of light, and thus on electromagnetism, which could have a different set of preferred frames. But using different assumptions about the special-relativistic frames (such as their being earth-fixed, or in free fall), one can derive different predictions for the gravitational redshift, that is, the way in which the frequency of light shifts as the light propagates through a gravitational field (cf. below). The actual measurements show that free-falling frames are the ones in which light propagates as it does in special relativity.[37] The generalization of this statement, namely that the laws of special relativity hold to good approximation in freely falling (and non-rotating) reference frames, is known as the Einstein equivalence principle, a crucial guiding principle for generalizing special-relativistic physics to include gravity.[38]
The same experimental data shows that time as measured by clocks in a gravitational field—proper time, to give the technical term—does not follow the rules of special relativity. In the language of spacetime geometry, it is not measured by the Minkowski metric. As in the Newtonian case, this is suggestive of a more general geometry. At small scales, all reference frames that are in free fall are equivalent, and approximately Minkowskian. Consequently, we are now dealing with a curved generalization of Minkowski space. The metric tensor that defines the geometry—in particular, how lengths and angles are measured—is not the Minkowski metric of special relativity, it is a generalization known as a semi- or pseudo-Riemannian metric. Furthermore, each Riemannian metric is naturally associated with one particular kind of connection, the Levi-Civita connection, and this is, in fact, the connection that satisfies the equivalence principle and makes space locally Minkowskian (that is, in suitable locally inertial coordinates, the metric is Minkowskian, and its first partial derivatives and the connection coefficients vanish).[39]
Einstein's equations
Having formulated the relativistic, geometric version of the effects of gravity, the question of gravity's source remains. In Newtonian gravity, the source is mass. In special relativity, mass turns out to be part of a more general quantity called the energy–momentum tensor, which includes both energy and momentum densities as well as stress: pressure and shear.[40] Using the equivalence principle, this tensor is readily generalized to curved spacetime. Drawing further upon the analogy with geometric Newtonian gravity, it is natural to assume that the field equation for gravity relates this tensor and the Ricci tensor, which describes a particular class of tidal effects: the change in volume for a small cloud of test particles that are initially at rest, and then fall freely. In special relativity, conservation of energy–momentum corresponds to the statement that the energy–momentum tensor is divergence-free. This formula, too, is readily generalized to curved spacetime by replacing partial derivatives with their curved-manifold counterparts, covariant derivatives studied in differential geometry. With this additional condition—the covariant divergence of the energy–momentum tensor, and hence of whatever is on the other side of the equation, is zero—the simplest nontrivial set of equations are what are called Einstein's (field) equations:
[math]\displaystyle{ G_{\mu\nu}\equiv R_{\mu\nu} - {\textstyle 1 \over 2}R\,g_{\mu\nu} = \kappa T_{\mu\nu}\, }[/math]
On the left-hand side is the Einstein tensor, [math]\displaystyle{ G_{\mu\nu} }[/math], which is symmetric and a specific divergence-free combination of the Ricci tensor [math]\displaystyle{ R_{\mu\nu} }[/math] and the metric. In particular,
- [math]\displaystyle{ R=g^{\mu\nu}R_{\mu\nu} }[/math]
is the curvature scalar. The Ricci tensor itself is related to the more general Riemann curvature tensor as
- [math]\displaystyle{ R_{\mu\nu}={R^\alpha}_{\mu\alpha\nu}. }[/math]
On the right-hand side, [math]\displaystyle{ \kappa }[/math] is a constant and [math]\displaystyle{ T_{\mu\nu} }[/math] is the energy–momentum tensor. All tensors are written in abstract index notation.[41] Matching the theory's prediction to observational results for planetary orbits or, equivalently, assuring that the weak-gravity, low-speed limit is Newtonian mechanics, the proportionality constant [math]\displaystyle{ \kappa }[/math] is found to be [math]\displaystyle{ \kappa=\frac{8\pi G}{c^4} }[/math], where [math]\displaystyle{ G }[/math] is the Newtonian constant of gravitation and [math]\displaystyle{ c }[/math] the speed of light in vacuum.[42] When there is no matter present, so that the energy–momentum tensor vanishes, the results are the vacuum Einstein equations,
- [math]\displaystyle{ R_{\mu\nu}=0. }[/math]
In general relativity, the world line of a particle free from all external, non-gravitational force is a particular type of geodesic in curved spacetime. In other words, a freely moving or falling particle always moves along a geodesic.
The geodesic equation is:
- [math]\displaystyle{ {d^2 x^\mu \over ds^2}+\Gamma^\mu {}_{\alpha \beta}{d x^\alpha \over ds}{d x^\beta \over ds}=0, }[/math]
where [math]\displaystyle{ s }[/math] is a scalar parameter of motion (e.g. the proper time), and [math]\displaystyle{ \Gamma^\mu {}_{\alpha \beta} }[/math] are Christoffel symbols (sometimes called the affine connection coefficients or Levi-Civita connection coefficients) which is symmetric in the two lower indices. Greek indices may take the values: 0, 1, 2, 3 and the summation convention is used for repeated indices [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math]. The quantity on the left-hand-side of this equation is the acceleration of a particle, and so this equation is analogous to Newton's laws of motion which likewise provide formulae for the acceleration of a particle. This equation of motion employs the Einstein notation, meaning that repeated indices are summed (i.e. from zero to three). The Christoffel symbols are functions of the four spacetime coordinates, and so are independent of the velocity or acceleration or other characteristics of a test particle whose motion is described by the geodesic equation.
Total force in general relativity
In general relativity, the effective gravitational potential energy of an object of mass m revolving around a massive central body M is given by[43][44]
- [math]\displaystyle{ U_f(r) =-\frac{GMm}{r}+\frac{L^{2}}{2mr^{2}}-\frac{GML^{2}}{mc^{2}r^{3}} }[/math]
A conservative total force can then be obtained as[citation needed]
- [math]\displaystyle{ F_f(r)=-\frac{GMm}{r^{2}}+\frac{L^{2}}{mr^{3}}-\frac{3GML^{2}}{mc^{2}r^{4}} }[/math]
where L is the angular momentum. The first term represents the force of Newtonian gravity, which is described by the inverse-square law. The second term represents the centrifugal force in the circular motion. The third term represents the relativistic effect.
Alternatives to general relativity
There are alternatives to general relativity built upon the same premises, which include additional rules and/or constraints, leading to different field equations. Examples are Whitehead's theory, Brans–Dicke theory, teleparallelism, f(R) gravity and Einstein–Cartan theory.[45]
Definition and basic applications
The derivation outlined in the previous section contains all the information needed to define general relativity, describe its key properties, and address a question of crucial importance in physics, namely how the theory can be used for model-building.
Definition and basic properties
General relativity is a metric theory of gravitation. At its core are Einstein's equations, which describe the relation between the geometry of a four-dimensional pseudo-Riemannian manifold representing spacetime, and the energy–momentum contained in that spacetime.[46] Phenomena that in classical mechanics are ascribed to the action of the force of gravity (such as free-fall, orbital motion, and spacecraft trajectories), correspond to inertial motion within a curved geometry of spacetime in general relativity; there is no gravitational force deflecting objects from their natural, straight paths. Instead, gravity corresponds to changes in the properties of space and time, which in turn changes the straightest-possible paths that objects will naturally follow.[47] The curvature is, in turn, caused by the energy–momentum of matter. Paraphrasing the relativist John Archibald Wheeler, spacetime tells matter how to move; matter tells spacetime how to curve.[48]
While general relativity replaces the scalar gravitational potential of classical physics by a symmetric rank-two tensor, the latter reduces to the former in certain limiting cases. For weak gravitational fields and slow speed relative to the speed of light, the theory's predictions converge on those of Newton's law of universal gravitation.[49]
As it is constructed using tensors, general relativity exhibits general covariance: its laws—and further laws formulated within the general relativistic framework—take on the same form in all coordinate systems.[50] Furthermore, the theory does not contain any invariant geometric background structures, i.e. it is background independent. It thus satisfies a more stringent general principle of relativity, namely that the laws of physics are the same for all observers.[51] Locally, as expressed in the equivalence principle, spacetime is Minkowskian, and the laws of physics exhibit local Lorentz invariance.[52]
Model-building
The core concept of general-relativistic model-building is that of a solution of Einstein's equations. Given both Einstein's equations and suitable equations for the properties of matter, such a solution consists of a specific semi-Riemannian manifold (usually defined by giving the metric in specific coordinates), and specific matter fields defined on that manifold. Matter and geometry must satisfy Einstein's equations, so in particular, the matter's energy–momentum tensor must be divergence-free. The matter must, of course, also satisfy whatever additional equations were imposed on its properties. In short, such a solution is a model universe that satisfies the laws of general relativity, and possibly additional laws governing whatever matter might be present.[53]
Einstein's equations are nonlinear partial differential equations and, as such, difficult to solve exactly.[54] Nevertheless, a number of exact solutions are known, although only a few have direct physical applications.[55] The best-known exact solutions, and also those most interesting from a physics point of view, are the Schwarzschild solution, the Reissner–Nordström solution and the Kerr metric, each corresponding to a certain type of black hole in an otherwise empty universe,[56] and the Friedmann–Lemaître–Robertson–Walker and de Sitter universes, each describing an expanding cosmos.[57] Exact solutions of great theoretical interest include the Gödel universe (which opens up the intriguing possibility of time travel in curved spacetimes), the Taub–NUT solution (a model universe that is homogeneous, but anisotropic), and anti-de Sitter space (which has recently come to prominence in the context of what is called the Maldacena conjecture).[58]
Given the difficulty of finding exact solutions, Einstein's field equations are also solved frequently by numerical integration on a computer, or by considering small perturbations of exact solutions. In the field of numerical relativity, powerful computers are employed to simulate the geometry of spacetime and to solve Einstein's equations for interesting situations such as two colliding black holes.[59] In principle, such methods may be applied to any system, given sufficient computer resources, and may address fundamental questions such as naked singularities. Approximate solutions may also be found by perturbation theories such as linearized gravity[60] and its generalization, the post-Newtonian expansion, both of which were developed by Einstein. The latter provides a systematic approach to solving for the geometry of a spacetime that contains a distribution of matter that moves slowly compared with the speed of light. The expansion involves a series of terms; the first terms represent Newtonian gravity, whereas the later terms represent ever smaller corrections to Newton's theory due to general relativity.[61] An extension of this expansion is the parametrized post-Newtonian (PPN) formalism, which allows quantitative comparisons between the predictions of general relativity and alternative theories.[62]
Consequences of Einstein's theory
General relativity has a number of physical consequences. Some follow directly from the theory's axioms, whereas others have become clear only in the course of many years of research that followed Einstein's initial publication.
Gravitational time dilation and frequency shift
Assuming that the equivalence principle holds,[63] gravity influences the passage of time. Light sent down into a gravity well is blueshifted, whereas light sent in the opposite direction (i.e., climbing out of the gravity well) is redshifted; collectively, these two effects are known as the gravitational frequency shift. More generally, processes close to a massive body run more slowly when compared with processes taking place farther away; this effect is known as gravitational time dilation.[64]
Gravitational redshift has been measured in the laboratory[65] and using astronomical observations.[66] Gravitational time dilation in the Earth's gravitational field has been measured numerous times using atomic clocks,[67] while ongoing validation is provided as a side effect of the operation of the Global Positioning System (GPS).[68] Tests in stronger gravitational fields are provided by the observation of binary pulsars.[69] All results are in agreement with general relativity.[70] However, at the current level of accuracy, these observations cannot distinguish between general relativity and other theories in which the equivalence principle is valid.[71]
Light deflection and gravitational time delay
General relativity predicts that the path of light will follow the curvature of spacetime as it passes near a star. This effect was initially confirmed by observing the light of stars or distant quasars being deflected as it passes the Sun.[72]
This and related predictions follow from the fact that light follows what is called a light-like or null geodesic—a generalization of the straight lines along which light travels in classical physics. Such geodesics are the generalization of the invariance of lightspeed in special relativity.[73] As one examines suitable model spacetimes (either the exterior Schwarzschild solution or, for more than a single mass, the post-Newtonian expansion),[74] several effects of gravity on light propagation emerge. Although the bending of light can also be derived by extending the universality of free fall to light,[75] the angle of deflection resulting from such calculations is only half the value given by general relativity.[76]
Closely related to light deflection is the Shapiro Time Delay, the phenomenon that light signals take longer to move through a gravitational field than they would in the absence of that field. There have been numerous successful tests of this prediction.[77] In the parameterized post-Newtonian formalism (PPN), measurements of both the deflection of light and the gravitational time delay determine a parameter called γ, which encodes the influence of gravity on the geometry of space.[78]
Gravitational waves
Predicted in 1916[79][80] by Albert Einstein, there are gravitational waves: ripples in the metric of spacetime that propagate at the speed of light. These are one of several analogies between weak-field gravity and electromagnetism in that, they are analogous to electromagnetic waves. On 11 February 2016, the Advanced LIGO team announced that they had directly detected gravitational waves from a pair of black holes merging.[81][82][83]
The simplest type of such a wave can be visualized by its action on a ring of freely floating particles. A sine wave propagating through such a ring towards the reader distorts the ring in a characteristic, rhythmic fashion (animated image to the right).[84] Since Einstein's equations are non-linear, arbitrarily strong gravitational waves do not obey linear superposition, making their description difficult. However, linear approximations of gravitational waves are sufficiently accurate to describe the exceedingly weak waves that are expected to arrive here on Earth from far-off cosmic events, which typically result in relative distances increasing and decreasing by [math]\displaystyle{ 10^{-21} }[/math] or less. Data analysis methods routinely make use of the fact that these linearized waves can be Fourier decomposed.[85]
Some exact solutions describe gravitational waves without any approximation, e.g., a wave train traveling through empty space[86] or Gowdy universes, varieties of an expanding cosmos filled with gravitational waves.[87] But for gravitational waves produced in astrophysically relevant situations, such as the merger of two black holes, numerical methods are presently the only way to construct appropriate models.[88]
Orbital effects and the relativity of direction
General relativity differs from classical mechanics in a number of predictions concerning orbiting bodies. It predicts an overall rotation (precession) of planetary orbits, as well as orbital decay caused by the emission of gravitational waves and effects related to the relativity of direction.
Precession of apsides
In general relativity, the apsides of any orbit (the point of the orbiting body's closest approach to the system's center of mass) will precess; the orbit is not an ellipse, but akin to an ellipse that rotates on its focus, resulting in a rose curve-like shape (see image). Einstein first derived this result by using an approximate metric representing the Newtonian limit and treating the orbiting body as a test particle. For him, the fact that his theory gave a straightforward explanation of Mercury's anomalous perihelion shift, discovered earlier by Urbain Le Verrier in 1859, was important evidence that he had at last identified the correct form of the gravitational field equations.[89]
The effect can also be derived by using either the exact Schwarzschild metric (describing spacetime around a spherical mass)[90] or the much more general post-Newtonian formalism.[91] It is due to the influence of gravity on the geometry of space and to the contribution of self-energy to a body's gravity (encoded in the nonlinearity of Einstein's equations).[92] Relativistic precession has been observed for all planets that allow for accurate precession measurements (Mercury, Venus, and Earth),[93] as well as in binary pulsar systems, where it is larger by five orders of magnitude.[94]
In general relativity the perihelion shift [math]\displaystyle{ \sigma }[/math], expressed in radians per revolution, is approximately given by[95]
- [math]\displaystyle{ \sigma=\frac {24\pi^3L^2} {T^2c^2(1-e^2)} \ , }[/math]
where:
- [math]\displaystyle{ L }[/math] is the semi-major axis
- [math]\displaystyle{ T }[/math] is the orbital period
- [math]\displaystyle{ c }[/math] is the speed of light in vacuum
- [math]\displaystyle{ e }[/math] is the orbital eccentricity
Orbital decay
According to general relativity, a binary system will emit gravitational waves, thereby losing energy. Due to this loss, the distance between the two orbiting bodies decreases, and so does their orbital period. Within the Solar System or for ordinary double stars, the effect is too small to be observable. This is not the case for a close binary pulsar, a system of two orbiting neutron stars, one of which is a pulsar: from the pulsar, observers on Earth receive a regular series of radio pulses that can serve as a highly accurate clock, which allows precise measurements of the orbital period. Because neutron stars are immensely compact, significant amounts of energy are emitted in the form of gravitational radiation.[97]
The first observation of a decrease in orbital period due to the emission of gravitational waves was made by Hulse and Taylor, using the binary pulsar PSR1913+16 they had discovered in 1974. This was the first detection of gravitational waves, albeit indirect, for which they were awarded the 1993 Nobel Prize in physics.[98] Since then, several other binary pulsars have been found, in particular the double pulsar PSR J0737−3039, where both stars are pulsars[99] and which was last reported to also be in agreement with general relativity in 2021 after 16 years of observations.[96]
Geodetic precession and frame-dragging
Several relativistic effects are directly related to the relativity of direction.[100] One is geodetic precession: the axis direction of a gyroscope in free fall in curved spacetime will change when compared, for instance, with the direction of light received from distant stars—even though such a gyroscope represents the way of keeping a direction as stable as possible ("parallel transport").[101] For the Moon–Earth system, this effect has been measured with the help of lunar laser ranging.[102] More recently, it has been measured for test masses aboard the satellite Gravity Probe B to a precision of better than 0.3%.[103][104]
Near a rotating mass, there are gravitomagnetic or frame-dragging effects. A distant observer will determine that objects close to the mass get "dragged around". This is most extreme for rotating black holes where, for any object entering a zone known as the ergosphere, rotation is inevitable.[105] Such effects can again be tested through their influence on the orientation of gyroscopes in free fall.[106] Somewhat controversial tests have been performed using the LAGEOS satellites, confirming the relativistic prediction.[107] Also the Mars Global Surveyor probe around Mars has been used.[108]
Interpretations
Neo-Lorentzian Interpretation
Examples of physicists who support neo-Lorentzian explanations of general relativity are Franco Selleri and Antony Valentini.[109]
Astrophysical applications
Gravitational lensing
The deflection of light by gravity is responsible for a new class of astronomical phenomena. If a massive object is situated between the astronomer and a distant target object with appropriate mass and relative distances, the astronomer will see multiple distorted images of the target. Such effects are known as gravitational lensing.[110] Depending on the configuration, scale, and mass distribution, there can be two or more images, a bright ring known as an Einstein ring, or partial rings called arcs.[111] The earliest example was discovered in 1979;[112] since then, more than a hundred gravitational lenses have been observed.[113] Even if the multiple images are too close to each other to be resolved, the effect can still be measured, e.g., as an overall brightening of the target object; a number of such "microlensing events" have been observed.[114]
Gravitational lensing has developed into a tool of observational astronomy. It is used to detect the presence and distribution of dark matter, provide a "natural telescope" for observing distant galaxies, and to obtain an independent estimate of the Hubble constant. Statistical evaluations of lensing data provide valuable insight into the structural evolution of galaxies.[115]
Gravitational-wave astronomy

Observations of binary pulsars provide strong indirect evidence for the existence of gravitational waves (see Orbital decay, above). Detection of these waves is a major goal of current relativity-related research.[116] Several land-based gravitational wave detectors are currently in operation, most notably the interferometric detectors GEO 600, LIGO (two detectors), TAMA 300 and VIRGO.[117] Various pulsar timing arrays are using millisecond pulsars to detect gravitational waves in the 10−9 to 10−6 hertz frequency range, which originate from binary supermassive blackholes.[118] A European space-based detector, eLISA / NGO, is currently under development,[119] with a precursor mission (LISA Pathfinder) having launched in December 2015.[120]
Observations of gravitational waves promise to complement observations in the electromagnetic spectrum.[121] They are expected to yield information about black holes and other dense objects such as neutron stars and white dwarfs, about certain kinds of supernova implosions, and about processes in the very early universe, including the signature of certain types of hypothetical cosmic string.[122] In February 2016, the Advanced LIGO team announced that they had detected gravitational waves from a black hole merger.[81][82][83]
Black holes and other compact objects
Whenever the ratio of an object's mass to its radius becomes sufficiently large, general relativity predicts the formation of a black hole, a region of space from which nothing, not even light, can escape. In the currently accepted models of stellar evolution, neutron stars of around 1.4 solar masses, and stellar black holes with a few to a few dozen solar masses, are thought to be the final state for the evolution of massive stars.[123] Usually a galaxy has one supermassive black hole with a few million to a few billion solar masses in its center,[124] and its presence is thought to have played an important role in the formation of the galaxy and larger cosmic structures.[125]
Astronomically, the most important property of compact objects is that they provide a supremely efficient mechanism for converting gravitational energy into electromagnetic radiation.[126] Accretion, the falling of dust or gaseous matter onto stellar or supermassive black holes, is thought to be responsible for some spectacularly luminous astronomical objects, notably diverse kinds of active galactic nuclei on galactic scales and stellar-size objects such as microquasars.[127] In particular, accretion can lead to relativistic jets, focused beams of highly energetic particles that are being flung into space at almost light speed.[128] General relativity plays a central role in modelling all these phenomena,[129] and observations provide strong evidence for the existence of black holes with the properties predicted by the theory.[130]
Black holes are also sought-after targets in the search for gravitational waves (cf. Gravitational waves, above). Merging black hole binaries should lead to some of the strongest gravitational wave signals reaching detectors here on Earth, and the phase directly before the merger ("chirp") could be used as a "standard candle" to deduce the distance to the merger events–and hence serve as a probe of cosmic expansion at large distances.[131] The gravitational waves produced as a stellar black hole plunges into a supermassive one should provide direct information about the supermassive black hole's geometry.[132]
Cosmology
The current models of cosmology are based on Einstein's field equations, which include the cosmological constant [math]\displaystyle{ \Lambda }[/math] since it has important influence on the large-scale dynamics of the cosmos,
- [math]\displaystyle{ R_{\mu\nu} - {\textstyle 1 \over 2}R\,g_{\mu\nu} + \Lambda\ g_{\mu\nu} = \frac{8\pi G}{c^{4}}\, T_{\mu\nu} }[/math]
where [math]\displaystyle{ g_{\mu\nu} }[/math] is the spacetime metric.[133] Isotropic and homogeneous solutions of these enhanced equations, the Friedmann–Lemaître–Robertson–Walker solutions,[134] allow physicists to model a universe that has evolved over the past 14 billion years from a hot, early Big Bang phase.[135] Once a small number of parameters (for example the universe's mean matter density) have been fixed by astronomical observation,[136] further observational data can be used to put the models to the test.[137] Predictions, all successful, include the initial abundance of chemical elements formed in a period of primordial nucleosynthesis,[138] the large-scale structure of the universe,[139] and the existence and properties of a "thermal echo" from the early cosmos, the cosmic background radiation.[140]
Astronomical observations of the cosmological expansion rate allow the total amount of matter in the universe to be estimated, although the nature of that matter remains mysterious in part. About 90% of all matter appears to be dark matter, which has mass (or, equivalently, gravitational influence), but does not interact electromagnetically and, hence, cannot be observed directly.[141] There is no generally accepted description of this new kind of matter, within the framework of known particle physics[142] or otherwise.[143] Observational evidence from redshift surveys of distant supernovae and measurements of the cosmic background radiation also show that the evolution of our universe is significantly influenced by a cosmological constant resulting in an acceleration of cosmic expansion or, equivalently, by a form of energy with an unusual equation of state, known as dark energy, the nature of which remains unclear.[144]
An inflationary phase,[145] an additional phase of strongly accelerated expansion at cosmic times of around 10−33 seconds, was hypothesized in 1980 to account for several puzzling observations that were unexplained by classical cosmological models, such as the nearly perfect homogeneity of the cosmic background radiation.[146] Recent measurements of the cosmic background radiation have resulted in the first evidence for this scenario.[147] However, there is a bewildering variety of possible inflationary scenarios, which cannot be restricted by current observations.[148] An even larger question is the physics of the earliest universe, prior to the inflationary phase and close to where the classical models predict the big bang singularity. An authoritative answer would require a complete theory of quantum gravity, which has not yet been developed[149] (cf. the section on quantum gravity, below).
Exotic solutions: time travel, warp drives
Kurt Gödel showed[150] that solutions to Einstein's equations exist that contain closed timelike curves (CTCs), which allow for loops in time. The solutions require extreme physical conditions unlikely ever to occur in practice, and it remains an open question whether further laws of physics will eliminate them completely. Since then, other—similarly impractical—GR solutions containing CTCs have been found, such as the Tipler cylinder and traversable wormholes. Stephen Hawking introduced chronology protection conjecture, which is an assumption beyond those of standard general relativity to prevent time travel.
Some exact solutions in general relativity such as Alcubierre drive present examples of warp drive but these solutions requires exotic matter distribution, and generally suffers from semiclassical instability. [151]
Advanced concepts
Asymptotic symmetries
The spacetime symmetry group for special relativity is the Poincaré group, which is a ten-dimensional group of three Lorentz boosts, three rotations, and four spacetime translations. It is logical to ask what symmetries if any might apply in General Relativity. A tractable case might be to consider the symmetries of spacetime as seen by observers located far away from all sources of the gravitational field. The naive expectation for asymptotically flat spacetime symmetries might be simply to extend and reproduce the symmetries of flat spacetime of special relativity, viz., the Poincaré group.
In 1962 Hermann Bondi, M. G. van der Burg, A. W. Metzner[152] and Rainer K. Sachs[153] addressed this asymptotic symmetry problem in order to investigate the flow of energy at infinity due to propagating gravitational waves. Their first step was to decide on some physically sensible boundary conditions to place on the gravitational field at light-like infinity to characterize what it means to say a metric is asymptotically flat, making no a priori assumptions about the nature of the asymptotic symmetry group—not even the assumption that such a group exists. Then after designing what they considered to be the most sensible boundary conditions, they investigated the nature of the resulting asymptotic symmetry transformations that leave invariant the form of the boundary conditions appropriate for asymptotically flat gravitational fields. What they found was that the asymptotic symmetry transformations actually do form a group and the structure of this group does not depend on the particular gravitational field that happens to be present. This means that, as expected, one can separate the kinematics of spacetime from the dynamics of the gravitational field at least at spatial infinity. The puzzling surprise in 1962 was their discovery of a rich infinite-dimensional group (the so-called BMS group) as the asymptotic symmetry group, instead of the finite-dimensional Poincaré group, which is a subgroup of the BMS group. Not only are the Lorentz transformations asymptotic symmetry transformations, there are also additional transformations that are not Lorentz transformations but are asymptotic symmetry transformations. In fact, they found an additional infinity of transformation generators known as supertranslations. This implies the conclusion that General Relativity (GR) does not reduce to special relativity in the case of weak fields at long distances. It turns out that the BMS symmetry, suitably modified, could be seen as a restatement of the universal soft graviton theorem in quantum field theory (QFT), which relates universal infrared (soft) QFT with GR asymptotic spacetime symmetries.[154]
Causal structure and global geometry
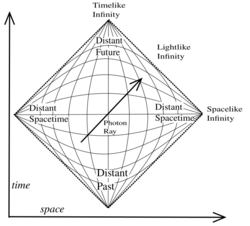
In general relativity, no material body can catch up with or overtake a light pulse. No influence from an event A can reach any other location X before light sent out at A to X. In consequence, an exploration of all light worldlines (null geodesics) yields key information about the spacetime's causal structure. This structure can be displayed using Penrose–Carter diagrams in which infinitely large regions of space and infinite time intervals are shrunk ("compactified") so as to fit onto a finite map, while light still travels along diagonals as in standard spacetime diagrams.[155]
Aware of the importance of causal structure, Roger Penrose and others developed what is known as global geometry. In global geometry, the object of study is not one particular solution (or family of solutions) to Einstein's equations. Rather, relations that hold true for all geodesics, such as the Raychaudhuri equation, and additional non-specific assumptions about the nature of matter (usually in the form of energy conditions) are used to derive general results.[156]
Horizons
Using global geometry, some spacetimes can be shown to contain boundaries called horizons, which demarcate one region from the rest of spacetime. The best-known examples are black holes: if mass is compressed into a sufficiently compact region of space (as specified in the hoop conjecture, the relevant length scale is the Schwarzschild radius[157]), no light from inside can escape to the outside. Since no object can overtake a light pulse, all interior matter is imprisoned as well. Passage from the exterior to the interior is still possible, showing that the boundary, the black hole's horizon, is not a physical barrier.[158]
Early studies of black holes relied on explicit solutions of Einstein's equations, notably the spherically symmetric Schwarzschild solution (used to describe a static black hole) and the axisymmetric Kerr solution (used to describe a rotating, stationary black hole, and introducing interesting features such as the ergosphere). Using global geometry, later studies have revealed more general properties of black holes. With time they become rather simple objects characterized by eleven parameters specifying: electric charge, mass–energy, linear momentum, angular momentum, and location at a specified time. This is stated by the black hole uniqueness theorem: "black holes have no hair", that is, no distinguishing marks like the hairstyles of humans. Irrespective of the complexity of a gravitating object collapsing to form a black hole, the object that results (having emitted gravitational waves) is very simple.[159]
Even more remarkably, there is a general set of laws known as black hole mechanics, which is analogous to the laws of thermodynamics. For instance, by the second law of black hole mechanics, the area of the event horizon of a general black hole will never decrease with time, analogous to the entropy of a thermodynamic system. This limits the energy that can be extracted by classical means from a rotating black hole (e.g. by the Penrose process).[160] There is strong evidence that the laws of black hole mechanics are, in fact, a subset of the laws of thermodynamics, and that the black hole area is proportional to its entropy.[161] This leads to a modification of the original laws of black hole mechanics: for instance, as the second law of black hole mechanics becomes part of the second law of thermodynamics, it is possible for black hole area to decrease—as long as other processes ensure that, overall, entropy increases. As thermodynamical objects with non-zero temperature, black holes should emit thermal radiation. Semi-classical calculations indicate that indeed they do, with the surface gravity playing the role of temperature in Planck's law. This radiation is known as Hawking radiation (cf. the quantum theory section, below).[162]
There are other types of horizons. In an expanding universe, an observer may find that some regions of the past cannot be observed ("particle horizon"), and some regions of the future cannot be influenced (event horizon).[163] Even in flat Minkowski space, when described by an accelerated observer (Rindler space), there will be horizons associated with a semi-classical radiation known as Unruh radiation.[164]
Singularities
Another general feature of general relativity is the appearance of spacetime boundaries known as singularities. Spacetime can be explored by following up on timelike and lightlike geodesics—all possible ways that light and particles in free fall can travel. But some solutions of Einstein's equations have "ragged edges"—regions known as spacetime singularities, where the paths of light and falling particles come to an abrupt end, and geometry becomes ill-defined. In the more interesting cases, these are "curvature singularities", where geometrical quantities characterizing spacetime curvature, such as the Ricci scalar, take on infinite values.[165] Well-known examples of spacetimes with future singularities—where worldlines end—are the Schwarzschild solution, which describes a singularity inside an eternal static black hole,[166] or the Kerr solution with its ring-shaped singularity inside an eternal rotating black hole.[167] The Friedmann–Lemaître–Robertson–Walker solutions and other spacetimes describing universes have past singularities on which worldlines begin, namely Big Bang singularities, and some have future singularities (Big Crunch) as well.[168]
Given that these examples are all highly symmetric—and thus simplified—it is tempting to conclude that the occurrence of singularities is an artifact of idealization.[169] The famous singularity theorems, proved using the methods of global geometry, say otherwise: singularities are a generic feature of general relativity, and unavoidable once the collapse of an object with realistic matter properties has proceeded beyond a certain stage[170] and also at the beginning of a wide class of expanding universes.[171] However, the theorems say little about the properties of singularities, and much of current research is devoted to characterizing these entities' generic structure (hypothesized e.g. by the BKL conjecture).[172] The cosmic censorship hypothesis states that all realistic future singularities (no perfect symmetries, matter with realistic properties) are safely hidden away behind a horizon, and thus invisible to all distant observers. While no formal proof yet exists, numerical simulations offer supporting evidence of its validity.[173]
Evolution equations
Each solution of Einstein's equation encompasses the whole history of a universe—it is not just some snapshot of how things are, but a whole, possibly matter-filled, spacetime. It describes the state of matter and geometry everywhere and at every moment in that particular universe. Due to its general covariance, Einstein's theory is not sufficient by itself to determine the time evolution of the metric tensor. It must be combined with a coordinate condition, which is analogous to gauge fixing in other field theories.[174]
To understand Einstein's equations as partial differential equations, it is helpful to formulate them in a way that describes the evolution of the universe over time. This is done in "3+1" formulations, where spacetime is split into three space dimensions and one time dimension. The best-known example is the ADM formalism.[175] These decompositions show that the spacetime evolution equations of general relativity are well-behaved: solutions always exist, and are uniquely defined, once suitable initial conditions have been specified.[176] Such formulations of Einstein's field equations are the basis of numerical relativity.[177]
Global and quasi-local quantities
The notion of evolution equations is intimately tied in with another aspect of general relativistic physics. In Einstein's theory, it turns out to be impossible to find a general definition for a seemingly simple property such as a system's total mass (or energy). The main reason is that the gravitational field—like any physical field—must be ascribed a certain energy, but that it proves to be fundamentally impossible to localize that energy.[178]
Nevertheless, there are possibilities to define a system's total mass, either using a hypothetical "infinitely distant observer" (ADM mass)[179] or suitable symmetries (Komar mass).[180] If one excludes from the system's total mass the energy being carried away to infinity by gravitational waves, the result is the Bondi mass at null infinity.[181] Just as in classical physics, it can be shown that these masses are positive.[182] Corresponding global definitions exist for momentum and angular momentum.[183] There have also been a number of attempts to define quasi-local quantities, such as the mass of an isolated system formulated using only quantities defined within a finite region of space containing that system. The hope is to obtain a quantity useful for general statements about isolated systems, such as a more precise formulation of the hoop conjecture.[184]
Relationship with quantum theory
If general relativity were considered to be one of the two pillars of modern physics, then quantum theory, the basis of understanding matter from elementary particles to solid-state physics, would be the other.[185] However, how to reconcile quantum theory with general relativity is still an open question.
Quantum field theory in curved spacetime
Ordinary quantum field theories, which form the basis of modern elementary particle physics, are defined in flat Minkowski space, which is an excellent approximation when it comes to describing the behavior of microscopic particles in weak gravitational fields like those found on Earth.[186] In order to describe situations in which gravity is strong enough to influence (quantum) matter, yet not strong enough to require quantization itself, physicists have formulated quantum field theories in curved spacetime. These theories rely on general relativity to describe a curved background spacetime, and define a generalized quantum field theory to describe the behavior of quantum matter within that spacetime.[187] Using this formalism, it can be shown that black holes emit a blackbody spectrum of particles known as Hawking radiation leading to the possibility that they evaporate over time.[188] As briefly mentioned above, this radiation plays an important role for the thermodynamics of black holes.[189]
Quantum gravity
The demand for consistency between a quantum description of matter and a geometric description of spacetime,[190] as well as the appearance of singularities (where curvature length scales become microscopic), indicate the need for a full theory of quantum gravity: for an adequate description of the interior of black holes, and of the very early universe, a theory is required in which gravity and the associated geometry of spacetime are described in the language of quantum physics.[191] Despite major efforts, no complete and consistent theory of quantum gravity is currently known, even though a number of promising candidates exist.[192][193]

Attempts to generalize ordinary quantum field theories, used in elementary particle physics to describe fundamental interactions, so as to include gravity have led to serious problems.[194] Some have argued that at low energies, this approach proves successful, in that it results in an acceptable effective (quantum) field theory of gravity.[195] At very high energies, however, the perturbative results are badly divergent and lead to models devoid of predictive power ("perturbative non-renormalizability").[196]
One attempt to overcome these limitations is string theory, a quantum theory not of point particles, but of minute one-dimensional extended objects.[197] The theory promises to be a unified description of all particles and interactions, including gravity;[198] the price to pay is unusual features such as six extra dimensions of space in addition to the usual three.[199] In what is called the second superstring revolution, it was conjectured that both string theory and a unification of general relativity and supersymmetry known as supergravity[200] form part of a hypothesized eleven-dimensional model known as M-theory, which would constitute a uniquely defined and consistent theory of quantum gravity.[201]
Another approach starts with the canonical quantization procedures of quantum theory. Using the initial-value-formulation of general relativity (cf. evolution equations above), the result is the Wheeler–deWitt equation (an analogue of the Schrödinger equation) which, regrettably, turns out to be ill-defined without a proper ultraviolet (lattice) cutoff.[202] However, with the introduction of what are now known as Ashtekar variables,[203] this leads to a promising model known as loop quantum gravity. Space is represented by a web-like structure called a spin network, evolving over time in discrete steps.[204]
Depending on which features of general relativity and quantum theory are accepted unchanged, and on what level changes are introduced,[205] there are numerous other attempts to arrive at a viable theory of quantum gravity, some examples being the lattice theory of gravity based on the Feynman Path Integral approach and Regge calculus,[192] dynamical triangulations,[206] causal sets,[207] twistor models[208] or the path integral based models of quantum cosmology.[209]
All candidate theories still have major formal and conceptual problems to overcome. They also face the common problem that, as yet, there is no way to put quantum gravity predictions to experimental tests (and thus to decide between the candidates where their predictions vary), although there is hope for this to change as future data from cosmological observations and particle physics experiments becomes available.[210]
Current status
General relativity has emerged as a highly successful model of gravitation and cosmology, which has so far passed many unambiguous observational and experimental tests. However, there are strong indications that the theory is incomplete.[211] The problem of quantum gravity and the question of the reality of spacetime singularities remain open.[212] Observational data that is taken as evidence for dark energy and dark matter could indicate the need for new physics.[213]
Even taken as is, general relativity is rich with possibilities for further exploration. Mathematical relativists seek to understand the nature of singularities and the fundamental properties of Einstein's equations,[214] while numerical relativists run increasingly powerful computer simulations (such as those describing merging black holes).[215] In February 2016, it was announced that the existence of gravitational waves was directly detected by the Advanced LIGO team on 14 September 2015.[83][216][217] A century after its introduction, general relativity remains a highly active area of research.[218]
See also
- Alcubierre drive – Hypothetical FTL transportation by warping space (warp drive)
- Alternatives to general relativity
- Contributors to general relativity
- Derivations of the Lorentz transformations
- Ehrenfest paradox
- Einstein–Hilbert action
- Einstein's thought experiments
- General relativity priority dispute
- Introduction to the mathematics of general relativity
- Nordström's theory of gravitation
- Ricci calculus – Tensor index notation for tensor-based calculations
- Timeline of gravitational physics and relativity
- Weak Gravity Conjecture
References
- ↑ "GW150914: LIGO Detects Gravitational Waves". http://www.black-holes.org/gw150914.
- ↑ 2.0 2.1 Landau & Lifshitz 1975, p. 228 "...the general theory of relativity...was established by Einstein, and represents probably the most beautiful of all existing physical theories."
- ↑ Poincaré 1905
- ↑ O'Connor, J.J.; Robertson, E.F. (May 1996). "General relativity"]. http://www-history.mcs.st-and.ac.uk/HistTopics/General_relativity.html. History Topics: Mathematical Physics Index, Scotland: School of Mathematics and Statistics, University of St. Andrews, http://www-history.mcs.st-and.ac.uk/Indexes/Math_Physics.html, retrieved 4 February 2015
- ↑ Pais 1982, ch. 9 to 15, Janssen 2005; an up-to-date collection of current research, including reprints of many of the original articles, is Renn 2007; an accessible overview can be found in Renn 2005, pp. 110ff. Einstein's original papers are found in Digital Einstein, volumes 4 and 6. An early key article is Einstein 1907, cf. Pais 1982, ch. 9. The publication featuring the field equations is Einstein 1915, cf. Pais 1982, ch. 11–15
- ↑ Moshe Carmeli (2008).Relativity: Modern Large-Scale Structures of the Cosmos. pp.92, 93.World Scientific Publishing
- ↑ Grossmann for the mathematical part and Einstein for the physical part (1913). Entwurf einer verallgemeinerten Relativitätstheorie und einer Theorie der Gravitation (Outline of a Generalized Theory of Relativity and of a Theory of Gravitation), Zeitschrift für Mathematik und Physik, 62, 225–261. English translate
- ↑ Schwarzschild 1916a, Schwarzschild 1916b and Reissner 1916 (later complemented in Nordström 1918)
- ↑ Einstein 1917, cf. Pais 1982, ch. 15e
- ↑ Hubble's original article is Hubble 1929; an accessible overview is given in Singh 2004, ch. 2–4
- ↑ As reported in Gamow 1970. Einstein's condemnation would prove to be premature, cf. the section Cosmology, below
- ↑ Pais 1982, pp. 253–254
- ↑ Kennefick 2005, Kennefick 2007
- ↑ Pais 1982, ch. 16
- ↑ Thorne 2003, p. 74
- ↑ Israel 1987, ch. 7.8–7.10, Thorne 1994, ch. 3–9
- ↑ Sections Orbital effects and the relativity of direction, Gravitational time dilation and frequency shift and Light deflection and gravitational time delay, and references therein
- ↑ Section Cosmology and references therein; the historical development is in Overbye 1999
- ↑ Wald 1984, p. 3
- ↑ Rovelli 2015, pp. 1–6 "General relativity is not just an extraordinarily beautiful physical theory providing the best description of the gravitational interaction we have so far. It is more."
- ↑ Chandrasekhar 1984, p. 6
- ↑ Engler 2002
- ↑ Albert Einstein (2011). Relativity – The Special and General Theory. Read Books Ltd. p. 4. ISBN 978-1-4474-9358-7. https://books.google.com/books?id=yhN9CgAAQBAJ. Extract of page 4
- ↑ The following exposition re-traces that of Ehlers 1973, sec. 1
- ↑ Al-Khalili, Jim (26 March 2021). "Gravity and Me: The force that shapes our lives". https://www.bbc.co.uk/programmes/b08kgv7f.
- ↑ Arnold 1989, ch. 1
- ↑ Ehlers 1973, pp. 5f
- ↑ Will 1993, sec. 2.4, Will 2006, sec. 2
- ↑ Wheeler 1990, ch. 2
- ↑ Ehlers 1973, sec. 1.2, Havas 1964, Künzle 1972. The simple thought experiment in question was first described in Heckmann & Schücking 1959
- ↑ Ehlers 1973, pp. 10f
- ↑ Good introductions are, in order of increasing presupposed knowledge of mathematics, Giulini 2005, Mermin 2005, and Rindler 1991; for accounts of precision experiments, cf. part IV of Ehlers & Lämmerzahl 2006
- ↑ An in-depth comparison between the two symmetry groups can be found in Giulini 2006
- ↑ Rindler 1991, sec. 22, Synge 1972, ch. 1 and 2
- ↑ Ehlers 1973, sec. 2.3
- ↑ Ehlers 1973, sec. 1.4, Schutz 1985, sec. 5.1
- ↑ Ehlers 1973, pp. 17ff; a derivation can be found in Mermin 2005, ch. 12. For the experimental evidence, cf. the section Gravitational time dilation and frequency shift, below
- ↑ Rindler 2001, sec. 1.13; for an elementary account, see Wheeler 1990, ch. 2; there are, however, some differences between the modern version and Einstein's original concept used in the historical derivation of general relativity, cf. Norton 1985
- ↑ Ehlers 1973, sec. 1.4 for the experimental evidence, see once more section Gravitational time dilation and frequency shift. Choosing a different connection with non-zero torsion leads to a modified theory known as Einstein–Cartan theory
- ↑ Ehlers 1973, p. 16, Kenyon 1990, sec. 7.2, Weinberg 1972, sec. 2.8
- ↑ Ehlers 1973, pp. 19–22; for similar derivations, see sections 1 and 2 of ch. 7 in Weinberg 1972. The Einstein tensor is the only divergence-free tensor that is a function of the metric coefficients, their first and second derivatives at most, and allows the spacetime of special relativity as a solution in the absence of sources of gravity, cf. Lovelock 1972. The tensors on both side are of second rank, that is, they can each be thought of as 4×4 matrices, each of which contains ten independent terms; hence, the above represents ten coupled equations. The fact that, as a consequence of geometric relations known as Bianchi identities, the Einstein tensor satisfies a further four identities reduces these to six independent equations, e.g. Schutz 1985, sec. 8.3
- ↑ Kenyon 1990, sec. 7.4
- ↑ Weinberg, Steven (1972). Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity. John Wiley. ISBN 978-0-471-92567-5.
- ↑ Cheng, Ta-Pei (2005). Relativity, Gravitation and Cosmology: a Basic Introduction. Oxford and New York: Oxford University Press. ISBN 978-0-19-852957-6.
- ↑ Brans & Dicke 1961, Weinberg 1972, sec. 3 in ch. 7, Goenner 2004, sec. 7.2, and Trautman 2006, respectively
- ↑ Wald 1984, ch. 4, Weinberg 1972, ch. 7 or, in fact, any other textbook on general relativity
- ↑ At least approximately, cf. Poisson 2004a
- ↑ Wheeler 1990, p. xi
- ↑ Wald 1984, sec. 4.4
- ↑ Wald 1984, sec. 4.1
- ↑ For the (conceptual and historical) difficulties in defining a general principle of relativity and separating it from the notion of general covariance, see Giulini 2007
- ↑ section 5 in ch. 12 of Weinberg 1972
- ↑ Introductory chapters of Stephani et al. 2003
- ↑ A review showing Einstein's equation in the broader context of other PDEs with physical significance is Geroch 1996
- ↑ For background information and a list of solutions, cf. Stephani et al. 2003; a more recent review can be found in MacCallum 2006
- ↑ Chandrasekhar 1983, ch. 3,5,6
- ↑ Narlikar 1993, ch. 4, sec. 3.3
- ↑ Brief descriptions of these and further interesting solutions can be found in Hawking & Ellis 1973, ch. 5
- ↑ Lehner 2002
- ↑ For instance Wald 1984, sec. 4.4
- ↑ Will 1993, sec. 4.1 and 4.2
- ↑ Will 2006, sec. 3.2, Will 1993, ch. 4
- ↑ Rindler 2001, pp. 24–26 vs. pp. 236–237 and Ohanian & Ruffini 1994, pp. 164–172. Einstein derived these effects using the equivalence principle as early as 1907, cf. Einstein 1907 and the description in Pais 1982, pp. 196–198
- ↑ Rindler 2001, pp. 24–26; Misner, Thorne & Wheeler 1973, § 38.5
- ↑ Pound–Rebka experiment, see Pound & Rebka 1959, Pound & Rebka 1960; Pound & Snider 1964; a list of further experiments is given in Ohanian & Ruffini 1994, table 4.1 on p. 186
- ↑ Greenstein, Oke & Shipman 1971; the most recent and most accurate Sirius B measurements are published in Barstow, Bond et al. 2005.
- ↑ Starting with the Hafele–Keating experiment, Hafele & Keating 1972a and Hafele & Keating 1972b, and culminating in the Gravity Probe A experiment; an overview of experiments can be found in Ohanian & Ruffini 1994, table 4.1 on p. 186
- ↑ GPS is continually tested by comparing atomic clocks on the ground and aboard orbiting satellites; for an account of relativistic effects, see Ashby 2002 and Ashby 2003
- ↑ Stairs 2003 and Kramer 2004
- ↑ General overviews can be found in section 2.1. of Will 2006; Will 2003, pp. 32–36; Ohanian & Ruffini 1994, sec. 4.2
- ↑ Ohanian & Ruffini 1994, pp. 164–172
- ↑ Cf. Kennefick 2005 for the classic early measurements by Arthur Eddington's expeditions. For an overview of more recent measurements, see Ohanian & Ruffini 1994, ch. 4.3. For the most precise direct modern observations using quasars, cf. Shapiro et al. 2004
- ↑ This is not an independent axiom; it can be derived from Einstein's equations and the Maxwell Lagrangian using a WKB approximation, cf. Ehlers 1973, sec. 5
- ↑ Blanchet 2006, sec. 1.3
- ↑ Rindler 2001, sec. 1.16; for the historical examples, Israel 1987, pp. 202–204; in fact, Einstein published one such derivation as Einstein 1907. Such calculations tacitly assume that the geometry of space is Euclidean, cf. Ehlers & Rindler 1997
- ↑ From the standpoint of Einstein's theory, these derivations take into account the effect of gravity on time, but not its consequences for the warping of space, cf. Rindler 2001, sec. 11.11
- ↑ For the Sun's gravitational field using radar signals reflected from planets such as Venus and Mercury, cf. Shapiro 1964, Weinberg 1972, ch. 8, sec. 7; for signals actively sent back by space probes (transponder measurements), cf. Bertotti, Iess & Tortora 2003; for an overview, see Ohanian & Ruffini 1994, table 4.4 on p. 200; for more recent measurements using signals received from a pulsar that is part of a binary system, the gravitational field causing the time delay being that of the other pulsar, cf. Stairs 2003, sec. 4.4
- ↑ Will 1993, sec. 7.1 and 7.2
- ↑ Einstein, A (22 June 1916). "Näherungsweise Integration der Feldgleichungen der Gravitation". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften Berlin (part 1): 688–696. Bibcode: 1916SPAW.......688E. http://einstein-annalen.mpiwg-berlin.mpg.de/related_texts/sitzungsberichte. Retrieved 12 February 2016.
- ↑ Einstein, A (31 January 1918). "Über Gravitationswellen". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften Berlin (part 1): 154–167. Bibcode: 1918SPAW.......154E. http://einstein-annalen.mpiwg-berlin.mpg.de/related_texts/sitzungsberichte. Retrieved 12 February 2016.
- ↑ 81.0 81.1 Castelvecchi, Davide; Witze, Witze (11 February 2016). "Einstein's gravitational waves found at last". Nature News. doi:10.1038/nature.2016.19361. http://www.nature.com/news/einstein-s-gravitational-waves-found-at-last-1.19361. Retrieved 11 February 2016.
- ↑ 82.0 82.1 B. P. Abbott (2016). "Observation of Gravitational Waves from a Binary Black Hole Merger". Physical Review Letters 116 (6): 061102. doi:10.1103/PhysRevLett.116.061102. PMID 26918975. Bibcode: 2016PhRvL.116f1102A.
- ↑ 83.0 83.1 83.2 "Gravitational waves detected 100 years after Einstein's prediction". 11 February 2016. https://www.nsf.gov/news/news_summ.jsp?cntn_id=137628.
- ↑ Most advanced textbooks on general relativity contain a description of these properties, e.g. Schutz 1985, ch. 9
- ↑ For example Jaranowski & Królak 2005
- ↑ Rindler 2001, ch. 13
- ↑ Gowdy 1971, Gowdy 1974
- ↑ See Lehner 2002 for a brief introduction to the methods of numerical relativity, and Seidel 1998 for the connection with gravitational wave astronomy
- ↑ Schutz 2003, pp. 48–49, Pais 1982, pp. 253–254
- ↑ Rindler 2001, sec. 11.9
- ↑ Will 1993, pp. 177–181
- ↑ In consequence, in the parameterized post-Newtonian formalism (PPN), measurements of this effect determine a linear combination of the terms β and γ, cf. Will 2006, sec. 3.5 and Will 1993, sec. 7.3
- ↑ The most precise measurements are VLBI measurements of planetary positions; see Will 1993, ch. 5, Will 2006, sec. 3.5, Anderson et al. 1992; for an overview, Ohanian & Ruffini 1994, pp. 406–407
- ↑ Kramer et al. 2006
- ↑ Dediu, Magdalena & Martín-Vide 2015, p. 141.
- ↑ 96.0 96.1 Kramer, M.; Stairs, I. H.; Manchester, R. N.; Wex, N.; Deller, A. T.; Coles, W. A.; Ali, M.; Burgay, M. et al. (13 December 2021). "Strong-Field Gravity Tests with the Double Pulsar" (in en). Physical Review X 11 (4): 041050. doi:10.1103/PhysRevX.11.041050. ISSN 2160-3308. Bibcode: 2021PhRvX..11d1050K. https://link.aps.org/doi/10.1103/PhysRevX.11.041050.
- ↑ Stairs 2003, Schutz 2003, pp. 317–321, Bartusiak 2000, pp. 70–86
- ↑ Weisberg & Taylor 2003; for the pulsar discovery, see Hulse & Taylor 1975; for the initial evidence for gravitational radiation, see Taylor 1994
- ↑ Kramer 2004
- ↑ Penrose 2004, § 14.5, Misner, Thorne & Wheeler 1973, § 11.4
- ↑ Weinberg 1972, sec. 9.6, Ohanian & Ruffini 1994, sec. 7.8
- ↑ Bertotti, Ciufolini & Bender 1987, Nordtvedt 2003
- ↑ Kahn 2007
- ↑ A mission description can be found in Everitt et al. 2001; a first post-flight evaluation is given in Everitt, Parkinson & Kahn 2007; further updates will be available on the mission website Kahn 1996–2012.
- ↑ Townsend 1997, sec. 4.2.1, Ohanian & Ruffini 1994, pp. 469–471
- ↑ Ohanian & Ruffini 1994, sec. 4.7, Weinberg 1972, sec. 9.7; for a more recent review, see Schäfer 2004
- ↑ Ciufolini & Pavlis 2004, Ciufolini, Pavlis & Peron 2006, Iorio 2009
- ↑ Iorio 2006, Iorio 2010
- ↑ Einstein, Relativity, and Absolute Simultaneity. London: Routledge. 2007. ISBN 978-1-134-00389-1.
- ↑ For overviews of gravitational lensing and its applications, see Ehlers, Falco & Schneider 1992 and Wambsganss 1998
- ↑ For a simple derivation, see Schutz 2003, ch. 23; cf. Narayan & Bartelmann 1997, sec. 3
- ↑ Walsh, Carswell & Weymann 1979
- ↑ Images of all the known lenses can be found on the pages of the CASTLES project, Kochanek et al. 2007
- ↑ Roulet & Mollerach 1997
- ↑ Narayan & Bartelmann 1997, sec. 3.7
- ↑ Barish 2005, Bartusiak 2000, Blair & McNamara 1997
- ↑ Hough & Rowan 2000
- ↑ Hobbs, George; Archibald, A.; Arzoumanian, Z.; Backer, D.; Bailes, M.; Bhat, N. D. R.; Burgay, M.; Burke-Spolaor, S. et al. (2010), "The international pulsar timing array project: using pulsars as a gravitational wave detector", Classical and Quantum Gravity 27 (8): 084013, doi:10.1088/0264-9381/27/8/084013, Bibcode: 2010CQGra..27h4013H
- ↑ Danzmann & Rüdiger 2003
- ↑ "LISA pathfinder overview". ESA. http://www.esa.int/esaSC/120397_index_0_m.html.
- ↑ Thorne 1995
- ↑ Cutler & Thorne 2002
- ↑ Miller 2002, lectures 19 and 21
- ↑ Celotti, Miller & Sciama 1999, sec. 3
- ↑ Springel et al. 2005 and the accompanying summary Gnedin 2005
- ↑ Blandford 1987, sec. 8.2.4
- ↑ For the basic mechanism, see Carroll & Ostlie 1996, sec. 17.2; for more about the different types of astronomical objects associated with this, cf. Robson 1996
- ↑ For a review, see Begelman, Blandford & Rees 1984. To a distant observer, some of these jets even appear to move faster than light; this, however, can be explained as an optical illusion that does not violate the tenets of relativity, see Rees 1966
- ↑ For stellar end states, cf. Oppenheimer & Snyder 1939 or, for more recent numerical work, Font 2003, sec. 4.1; for supernovae, there are still major problems to be solved, cf. Buras et al. 2003; for simulating accretion and the formation of jets, cf. Font 2003, sec. 4.2. Also, relativistic lensing effects are thought to play a role for the signals received from X-ray pulsars, cf. Kraus 1998
- ↑ The evidence includes limits on compactness from the observation of accretion-driven phenomena ("Eddington luminosity"), see Celotti, Miller & Sciama 1999, observations of stellar dynamics in the center of our own Milky Way galaxy, cf. Schödel et al. 2003, and indications that at least some of the compact objects in question appear to have no solid surface, which can be deduced from the examination of X-ray bursts for which the central compact object is either a neutron star or a black hole; cf. Remillard et al. 2006 for an overview, Narayan 2006, sec. 5. Observations of the "shadow" of the Milky Way galaxy's central black hole horizon are eagerly sought for, cf. Falcke, Melia & Agol 2000
- ↑ Dalal et al. 2006
- ↑ Barack & Cutler 2004
- ↑ Einstein 1917; cf. Pais 1982, pp. 285–288
- ↑ Carroll 2001, ch. 2
- ↑ Bergström & Goobar 2003, ch. 9–11; use of these models is justified by the fact that, at large scales of around hundred million light-years and more, our own universe indeed appears to be isotropic and homogeneous, cf. Peebles et al. 1991
- ↑ E.g. with WMAP data, see Spergel et al. 2003
- ↑ These tests involve the separate observations detailed further on, see, e.g., fig. 2 in Bridle et al. 2003
- ↑ Peebles 1966; for a recent account of predictions, see Coc, Vangioni‐Flam et al. 2004; an accessible account can be found in Weiss 2006; compare with the observations in Olive & Skillman 2004, Bania, Rood & Balser 2002, O'Meara et al. 2001, and Charbonnel & Primas 2005
- ↑ Lahav & Suto 2004, Bertschinger 1998, Springel et al. 2005
- ↑ Alpher & Herman 1948, for a pedagogical introduction, see Bergström & Goobar 2003, ch. 11; for the initial detection, see Penzias & Wilson 1965 and, for precision measurements by satellite observatories, Mather et al. 1994 (COBE) and Bennett et al. 2003 (WMAP). Future measurements could also reveal evidence about gravitational waves in the early universe; this additional information is contained in the background radiation's polarization, cf. Kamionkowski, Kosowsky & Stebbins 1997 and Seljak & Zaldarriaga 1997
- ↑ Evidence for this comes from the determination of cosmological parameters and additional observations involving the dynamics of galaxies and galaxy clusters cf. Peebles 1993, ch. 18, evidence from gravitational lensing, cf. Peacock 1999, sec. 4.6, and simulations of large-scale structure formation, see Springel et al. 2005
- ↑ Peacock 1999, ch. 12, Peskin 2007; in particular, observations indicate that all but a negligible portion of that matter is not in the form of the usual elementary particles ("non-baryonic matter"), cf. Peacock 1999, ch. 12
- ↑ Namely, some physicists have questioned whether or not the evidence for dark matter is, in fact, evidence for deviations from the Einsteinian (and the Newtonian) description of gravity cf. the overview in Mannheim 2006, sec. 9
- ↑ Carroll 2001; an accessible overview is given in Caldwell 2004. Here, too, scientists have argued that the evidence indicates not a new form of energy, but the need for modifications in our cosmological models, cf. Mannheim 2006, sec. 10; aforementioned modifications need not be modifications of general relativity, they could, for example, be modifications in the way we treat the inhomogeneities in the universe, cf. Buchert 2008
- ↑ A good introduction is Linde 2005; for a more recent review, see Linde 2006
- ↑ More precisely, these are the flatness problem, the horizon problem, and the monopole problem; a pedagogical introduction can be found in Narlikar 1993, sec. 6.4, see also Börner 1993, sec. 9.1
- ↑ Spergel et al. 2007, sec. 5,6
- ↑ More concretely, the potential function that is crucial to determining the dynamics of the inflaton is simply postulated, but not derived from an underlying physical theory
- ↑ Brandenberger 2008, sec. 2
- ↑ Gödel 1949
- ↑ Finazzi, Stefano; Liberati, Stefano; Barceló, Carlos (15 June 2009). "Semiclassical instability of dynamical warp drives" (in en-US). Physical Review D 79 (12): 124017. doi:10.1103/PhysRevD.79.124017. Bibcode: 2009PhRvD..79l4017F.
- ↑ Bondi, H.; Van der Burg, M.G.J.; Metzner, A. (1962). "Gravitational waves in general relativity: VII. Waves from axisymmetric isolated systems". Proceedings of the Royal Society of London A A269 (1336): 21–52. doi:10.1098/rspa.1962.0161. Bibcode: 1962RSPSA.269...21B.
- ↑ Sachs, R. (1962). "Asymptotic symmetries in gravitational theory". Physical Review 128 (6): 2851–2864. doi:10.1103/PhysRev.128.2851. Bibcode: 1962PhRv..128.2851S.
- ↑ Strominger, Andrew (2017). "Lectures on the Infrared Structure of Gravity and Gauge Theory". arXiv:1703.05448 [hep-th].
...redacted transcript of a course given by the author at Harvard in spring semester 2016. It contains a pedagogical overview of recent developments connecting the subjects of soft theorems, the memory effect and asymptotic symmetries in four-dimensional QED, nonabelian gauge theory and gravity with applications to black holes. To be published Princeton University Press, 158 pages.
- ↑ Frauendiener 2004, Wald 1984, sec. 11.1, Hawking & Ellis 1973, sec. 6.8, 6.9
- ↑ Wald 1984, sec. 9.2–9.4 and Hawking & Ellis 1973, ch. 6
- ↑ Thorne 1972; for more recent numerical studies, see Berger 2002, sec. 2.1
- ↑ Israel 1987. A more exact mathematical description distinguishes several kinds of horizon, notably event horizons and apparent horizons cf. Hawking & Ellis 1973, pp. 312–320 or Wald 1984, sec. 12.2; there are also more intuitive definitions for isolated systems that do not require knowledge of spacetime properties at infinity, cf. Ashtekar & Krishnan 2004
- ↑ For first steps, cf. Israel 1971; see Hawking & Ellis 1973, sec. 9.3 or Heusler 1996, ch. 9 and 10 for a derivation, and Heusler 1998 as well as Beig & Chruściel 2006 as overviews of more recent results
- ↑ The laws of black hole mechanics were first described in Bardeen, Carter & Hawking 1973; a more pedagogical presentation can be found in Carter 1979; for a more recent review, see Wald 2001, ch. 2. A thorough, book-length introduction including an introduction to the necessary mathematics Poisson 2004. For the Penrose process, see Penrose 1969
- ↑ Bekenstein 1973, Bekenstein 1974
- ↑ The fact that black holes radiate, quantum mechanically, was first derived in Hawking 1975; a more thorough derivation can be found in Wald 1975. A review is given in Wald 2001, ch. 3
- ↑ Narlikar 1993, sec. 4.4.4, 4.4.5
- ↑ Horizons: cf. Rindler 2001, sec. 12.4. Unruh effect: Unruh 1976, cf. Wald 2001, ch. 3
- ↑ Hawking & Ellis 1973, sec. 8.1, Wald 1984, sec. 9.1
- ↑ Townsend 1997, ch. 2; a more extensive treatment of this solution can be found in Chandrasekhar 1983, ch. 3
- ↑ Townsend 1997, ch. 4; for a more extensive treatment, cf. Chandrasekhar 1983, ch. 6
- ↑ Ellis & Van Elst 1999; a closer look at the singularity itself is taken in Börner 1993, sec. 1.2
- ↑ Here one should remind to the well-known fact that the important "quasi-optical" singularities of the so-called eikonal approximations of many wave equations, namely the "caustics", are resolved into finite peaks beyond that approximation.
- ↑ Namely when there are trapped null surfaces, cf. Penrose 1965
- ↑ Hawking 1966
- ↑ The conjecture was made in Belinskii, Khalatnikov & Lifschitz 1971; for a more recent review, see Berger 2002. An accessible exposition is given by Garfinkle 2007
- ↑ The restriction to future singularities naturally excludes initial singularities such as the big bang singularity, which in principle be visible to observers at later cosmic time. The cosmic censorship conjecture was first presented in Penrose 1969; a textbook-level account is given in Wald 1984, pp. 302–305. For numerical results, see the review Berger 2002, sec. 2.1
- ↑ Hawking & Ellis 1973, sec. 7.1
- ↑ Arnowitt, Deser & Misner 1962; for a pedagogical introduction, see Misner, Thorne & Wheeler 1973, § 21.4–§ 21.7
- ↑ Fourès-Bruhat 1952 and Bruhat 1962; for a pedagogical introduction, see Wald 1984, ch. 10; an online review can be found in Reula 1998
- ↑ Gourgoulhon 2007; for a review of the basics of numerical relativity, including the problems arising from the peculiarities of Einstein's equations, see Lehner 2001
- ↑ Misner, Thorne & Wheeler 1973, § 20.4
- ↑ Arnowitt, Deser & Misner 1962
- ↑ Komar 1959; for a pedagogical introduction, see Wald 1984, sec. 11.2; although defined in a totally different way, it can be shown to be equivalent to the ADM mass for stationary spacetimes, cf. Ashtekar & Magnon-Ashtekar 1979
- ↑ For a pedagogical introduction, see Wald 1984, sec. 11.2
- ↑ Wald 1984, p. 295 and refs therein; this is important for questions of stability—if there were negative mass states, then flat, empty Minkowski space, which has mass zero, could evolve into these states
- ↑ Townsend 1997, ch. 5
- ↑ Such quasi-local mass–energy definitions are the Hawking energy, Geroch energy, or Penrose's quasi-local energy–momentum based on twistor methods; cf. the review article Szabados 2004
- ↑ An overview of quantum theory can be found in standard textbooks such as Messiah 1999; a more elementary account is given in Hey & Walters 2003
- ↑ Ramond 1990, Weinberg 1995, Peskin & Schroeder 1995; a more accessible overview is Auyang 1995
- ↑ Wald 1994, Birrell & Davies 1984
- ↑ For Hawking radiation Hawking 1975, Wald 1975; an accessible introduction to black hole evaporation can be found in Traschen 2000
- ↑ Wald 2001, ch. 3
- ↑ Put simply, matter is the source of spacetime curvature, and once matter has quantum properties, we can expect spacetime to have them as well. Cf. Carlip 2001, sec. 2
- ↑ Schutz 2003, p. 407
- ↑ 192.0 192.1 Hamber 2009
- ↑ A timeline and overview can be found in Rovelli 2000
- ↑ 't Hooft & Veltman 1974
- ↑ Donoghue 1995
- ↑ In particular, a perturbative technique known as renormalization, an integral part of deriving predictions which take into account higher-energy contributions, cf. Weinberg 1996, ch. 17, 18, fails in this case; cf. Veltman 1975, Goroff & Sagnotti 1985; for a recent comprehensive review of the failure of perturbative renormalizability for quantum gravity see Hamber 2009
- ↑ An accessible introduction at the undergraduate level can be found in Zwiebach 2004; more complete overviews can be found in Polchinski 1998a and Polchinski 1998b
- ↑ At the energies reached in current experiments, these strings are indistinguishable from point-like particles, but, crucially, different modes of oscillation of one and the same type of fundamental string appear as particles with different (electric and other) charges, e.g. Ibanez 2000. The theory is successful in that one mode will always correspond to a graviton, the messenger particle of gravity, e.g. Green, Schwarz & Witten 1987, sec. 2.3, 5.3
- ↑ Green, Schwarz & Witten 1987, sec. 4.2
- ↑ Weinberg 2000, ch. 31
- ↑ Townsend 1996, Duff 1996
- ↑ Kuchař 1973, sec. 3
- ↑ These variables represent geometric gravity using mathematical analogues of electric and magnetic fields; cf. Ashtekar 1986, Ashtekar 1987
- ↑ For a review, see Thiemann 2007; more extensive accounts can be found in Rovelli 1998, Ashtekar & Lewandowski 2004 as well as in the lecture notes Thiemann 2003
- ↑ Isham 1994, Sorkin 1997
- ↑ Loll 1998
- ↑ Sorkin 2005
- ↑ Penrose 2004, ch. 33 and refs therein
- ↑ Hawking 1987
- ↑ Ashtekar 2007, Schwarz 2007
- ↑ Maddox 1998, pp. 52–59, 98–122; Penrose 2004, sec. 34.1, ch. 30
- ↑ section Quantum gravity, above
- ↑ section Cosmology, above
- ↑ Friedrich 2005
- ↑ A review of the various problems and the techniques being developed to overcome them, see Lehner 2002
- ↑ See Bartusiak 2000 for an account up to that year; up-to-date news can be found on the websites of major detector collaborations such as GEO600 and LIGO
- ↑ For the most recent papers on gravitational wave polarizations of inspiralling compact binaries, see Blanchet et al. 2008, and Arun et al. 2008; for a review of work on compact binaries, see Blanchet 2006 and Futamase & Itoh 2006; for a general review of experimental tests of general relativity, see Will 2006
- ↑ See, e.g., the Living Reviews in Relativity journal.
Bibliography
- Alpher, R. A.; Herman, R. C. (1948), "Evolution of the universe", Nature 162 (4124): 774–775, doi:10.1038/162774b0, Bibcode: 1948Natur.162..774A
- Anderson, J. D.; Campbell, J. K.; Jurgens, R. F.; Lau, E. L. (1992), "Recent developments in solar-system tests of general relativity", in Sato, H.; Nakamura, T., Proceedings of the Sixth Marcel Großmann Meeting on General Relativity, World Scientific, pp. 353–355, ISBN 978-981-02-0950-6
- Arnold, V. I. (1989), Mathematical Methods of Classical Mechanics, Springer, ISBN 978-3-540-96890-0
- Arnowitt, Richard; Deser, Stanley; Misner, Charles W. (1962), "The dynamics of general relativity", in Witten, Louis, Gravitation: An Introduction to Current Research, Wiley, pp. 227–265
- Arun, K.G.; Blanchet, L.; Iyer, B. R.; Qusailah, M. S. S. (2008), "Inspiralling compact binaries in quasi-elliptical orbits: The complete 3PN energy flux", Physical Review D 77 (6): 064035, doi:10.1103/PhysRevD.77.064035, Bibcode: 2008PhRvD..77f4035A
- Ashby, Neil (2002), "Relativity and the Global Positioning System", Physics Today 55 (5): 41–47, doi:10.1063/1.1485583, Bibcode: 2002PhT....55e..41A, http://www.ipgp.jussieu.fr/~tarantola/Files/Professional/GPS/Neil_Ashby_Relativity_GPS.pdf
- Ashby, Neil (2003), "Relativity in the Global Positioning System", Living Reviews in Relativity 6 (1): 1, doi:10.12942/lrr-2003-1, PMID 28163638, PMC 5253894, Bibcode: 2003LRR.....6....1A, http://relativity.livingreviews.org/Articles/lrr-2003-1/index.html, retrieved 6 July 2007
- Ashtekar, Abhay (1986), "New variables for classical and quantum gravity", Phys. Rev. Lett. 57 (18): 2244–2247, doi:10.1103/PhysRevLett.57.2244, PMID 10033673, Bibcode: 1986PhRvL..57.2244A
- Ashtekar, Abhay (1987), "New Hamiltonian formulation of general relativity", Phys. Rev. D36 (6): 1587–1602, doi:10.1103/PhysRevD.36.1587, PMID 9958340, Bibcode: 1987PhRvD..36.1587A
- Ashtekar, Abhay (2007), "Loop Quantum Gravity: Four Recent Advances and a Dozen Frequently Asked Questions", The Eleventh Marcel Grossmann Meeting – on Recent Developments in Theoretical and Experimental General Relativity, Gravitation and Relativistic Field Theories – Proceedings of the MG11 Meeting on General Relativity: 126, doi:10.1142/9789812834300_0008, ISBN 978-981-283-426-3, Bibcode: 2008mgm..conf..126A
- Ashtekar, Abhay; Krishnan, Badri (2004), "Isolated and Dynamical Horizons and Their Applications", Living Reviews in Relativity 7 (1): 10, doi:10.12942/lrr-2004-10, PMID 28163644, Bibcode: 2004LRR.....7...10A
- Ashtekar, Abhay; Lewandowski, Jerzy (2004), "Background Independent Quantum Gravity: A Status Report", Class. Quantum Grav. 21 (15): R53–R152, doi:10.1088/0264-9381/21/15/R01, Bibcode: 2004CQGra..21R..53A
- Ashtekar, Abhay; Magnon-Ashtekar, Anne (1979), "On conserved quantities in general relativity", Journal of Mathematical Physics 20 (5): 793–800, doi:10.1063/1.524151, Bibcode: 1979JMP....20..793A
- Auyang, Sunny Y. (1995), How is Quantum Field Theory Possible?, Oxford University Press, ISBN 978-0-19-509345-2
- Bania, T. M.; Rood, R. T.; Balser, D. S. (2002), "The cosmological density of baryons from observations of 3He+ in the Milky Way", Nature 415 (6867): 54–57, doi:10.1038/415054a, PMID 11780112, Bibcode: 2002Natur.415...54B
- Barack, Leor; Cutler, Curt (2004), "LISA Capture Sources: Approximate Waveforms, Signal-to-Noise Ratios, and Parameter Estimation Accuracy", Phys. Rev. D69 (8): 082005, doi:10.1103/PhysRevD.69.082005, Bibcode: 2004PhRvD..69h2005B
- Bardeen, J. M.; Carter, B.; Hawking, S. W. (1973), "The Four Laws of Black Hole Mechanics", Comm. Math. Phys. 31 (2): 161–170, doi:10.1007/BF01645742, Bibcode: 1973CMaPh..31..161B, http://projecteuclid.org/euclid.cmp/1103858973
- Barish, Barry (2005), "Towards detection of gravitational waves", in Florides, P.; Nolan, B.; Ottewil, A., General Relativity and Gravitation. Proceedings of the 17th International Conference, World Scientific, pp. 24–34, ISBN 978-981-256-424-5, Bibcode: 2005grg..conf.....F
- Barstow, M.; Bond, Howard E.; Holberg, J. B.; Burleigh, M. R.; Hubeny, I.; Koester, D. (2005), "Hubble Space Telescope Spectroscopy of the Balmer lines in Sirius B", Mon. Not. R. Astron. Soc. 362 (4): 1134–1142, doi:10.1111/j.1365-2966.2005.09359.x, Bibcode: 2005MNRAS.362.1134B
- Bartusiak, Marcia (2000), Einstein's Unfinished Symphony: Listening to the Sounds of Space-Time, Berkley, ISBN 978-0-425-18620-6
- Begelman, Mitchell C.; Blandford, Roger D.; Rees, Martin J. (1984), "Theory of extragalactic radio sources", Rev. Mod. Phys. 56 (2): 255–351, doi:10.1103/RevModPhys.56.255, Bibcode: 1984RvMP...56..255B
- Beig, Robert; Chruściel, Piotr T. (2006), "Stationary black holes", in Françoise, J.-P.; Naber, G.; Tsou, T.S., Encyclopedia of Mathematical Physics, Volume 2, Elsevier, p. 2041, ISBN 978-0-12-512660-1, Bibcode: 2005gr.qc.....2041B
- Bekenstein, Jacob D. (1973), "Black Holes and Entropy", Phys. Rev. D7 (8): 2333–2346, doi:10.1103/PhysRevD.7.2333, Bibcode: 1973PhRvD...7.2333B
- Bekenstein, Jacob D. (1974), "Generalized Second Law of Thermodynamics in Black-Hole Physics", Phys. Rev. D9 (12): 3292–3300, doi:10.1103/PhysRevD.9.3292, Bibcode: 1974PhRvD...9.3292B
- Belinskii, V. A.; Khalatnikov, I. M.; Lifschitz, E. M. (1971), "Oscillatory approach to the singular point in relativistic cosmology", Advances in Physics 19 (80): 525–573, doi:10.1080/00018737000101171, Bibcode: 1970AdPhy..19..525B; original paper in Russian: Belinsky, V. A.; Lifshits, I. M.; Khalatnikov, E. M. (1970), "Колебательный Режим Приближения К Особой Точке В Релятивистской Космологии", Uspekhi Fizicheskikh Nauk 102 (11): 463–500, doi:10.3367/ufnr.0102.197011d.0463, Bibcode: 1970UsFiN.102..463B
- Bennett, C. L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; Limon, M.; Meyer, S. S.; Page, L. et al. (2003), "First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Preliminary Maps and Basic Results", Astrophys. J. Suppl. Ser. 148 (1): 1–27, doi:10.1086/377253, Bibcode: 2003ApJS..148....1B
- Berger (2002), "Numerical Approaches to Spacetime Singularities", Living Reviews in Relativity 5 (1): 1, doi:10.12942/lrr-2002-1, PMID 28179859, Bibcode: 2002LRR.....5....1B
- Bergström, Lars; Goobar, Ariel (2003), Cosmology and Particle Astrophysics (2nd ed.), Wiley & Sons, ISBN 978-3-540-43128-2, https://archive.org/details/cosmologyparticl0000berg
- Bertotti, Bruno; Ciufolini, Ignazio; Bender, Peter L. (1987), "New test of general relativity: Measurement of de Sitter geodetic precession rate for lunar perigee", Physical Review Letters 58 (11): 1062–1065, doi:10.1103/PhysRevLett.58.1062, PMID 10034329, Bibcode: 1987PhRvL..58.1062B
- Bertotti, Bruno; Iess, L.; Tortora, P. (2003), "A test of general relativity using radio links with the Cassini spacecraft", Nature 425 (6956): 374–376, doi:10.1038/nature01997, PMID 14508481, Bibcode: 2003Natur.425..374B
- Bertschinger, Edmund (1998), "Simulations of structure formation in the universe", Annu. Rev. Astron. Astrophys. 36 (1): 599–654, doi:10.1146/annurev.astro.36.1.599, Bibcode: 1998ARA&A..36..599B
- Birrell, N. D.; Davies, P. C. (1984), Quantum Fields in Curved Space, Cambridge University Press, ISBN 978-0-521-27858-4
- Blair, David; McNamara, Geoff (1997), Ripples on a Cosmic Sea. The Search for Gravitational Waves, Perseus, ISBN 978-0-7382-0137-5, https://archive.org/details/isbn_9780738201375
- Blanchet, L.; Faye, G.; Iyer, B. R.; Sinha, S. (2008), "The third post-Newtonian gravitational wave polarisations and associated spherical harmonic modes for inspiralling compact binaries in quasi-circular orbits", Classical and Quantum Gravity 25 (16): 165003, doi:10.1088/0264-9381/25/16/165003, Bibcode: 2008CQGra..25p5003B
- Blanchet, Luc (2006), "Gravitational Radiation from Post-Newtonian Sources and Inspiralling Compact Binaries", Living Reviews in Relativity 9 (1): 4, doi:10.12942/lrr-2006-4, PMID 28179874, Bibcode: 2006LRR.....9....4B
- Blandford, R. D. (1987), "Astrophysical Black Holes", in Hawking, Stephen W.; Israel, Werner, 300 Years of Gravitation, Cambridge University Press, pp. 277–329, ISBN 978-0-521-37976-2
- Börner, Gerhard (1993), The Early Universe. Facts and Fiction, Springer, ISBN 978-0-387-56729-7
- Brandenberger, Robert H. (2008), "Conceptual problems of inflationary cosmology and a new approach to cosmological structure formation", in Lemoine, Martin; Martin, Jerome; Peter, Patrick, Inflationary Cosmology, Lecture Notes in Physics, 738, pp. 393–424, doi:10.1007/978-3-540-74353-8_11, ISBN 978-3-540-74352-1, Bibcode: 2007LNP...738..393B
- Brans, C. H.; Dicke, R. H. (1961), "Mach's Principle and a Relativistic Theory of Gravitation", Physical Review 124 (3): 925–935, doi:10.1103/PhysRev.124.925, Bibcode: 1961PhRv..124..925B
- Bridle, Sarah L.; Lahav, Ofer; Ostriker, Jeremiah P.; Steinhardt, Paul J. (2003), "Precision Cosmology? Not Just Yet", Science 299 (5612): 1532–1533, doi:10.1126/science.1082158, PMID 12624255, Bibcode: 2003Sci...299.1532B
- Bruhat, Yvonne (1962), "The Cauchy Problem", in Witten, Louis, Gravitation: An Introduction to Current Research, Wiley, p. 130, ISBN 978-1-114-29166-9
- Buchert, Thomas (2008), "Dark Energy from Structure—A Status Report", General Relativity and Gravitation 40 (2–3): 467–527, doi:10.1007/s10714-007-0554-8, Bibcode: 2008GReGr..40..467B
- Buras, R.; Rampp, M.; Janka, H.-Th.; Kifonidis, K. (2003), "Improved Models of Stellar Core Collapse and Still no Explosions: What is Missing?", Phys. Rev. Lett. 90 (24): 241101, doi:10.1103/PhysRevLett.90.241101, PMID 12857181, Bibcode: 2003PhRvL..90x1101B
- Caldwell, Robert R. (2004), "Dark Energy", Physics World 17 (5): 37–42, doi:10.1088/2058-7058/17/5/36
- Carlip, Steven (2001), "Quantum Gravity: a Progress Report", Rep. Prog. Phys. 64 (8): 885–942, doi:10.1088/0034-4885/64/8/301, Bibcode: 2001RPPh...64..885C
- Carroll, Bradley W.; Ostlie, Dale A. (1996), An Introduction to Modern Astrophysics, Addison-Wesley, ISBN 978-0-201-54730-6
- Carroll, Sean M. (2001), "The Cosmological Constant", Living Reviews in Relativity 4 (1): 1, doi:10.12942/lrr-2001-1, PMID 28179856, Bibcode: 2001LRR.....4....1C
- Carter, Brandon (1979), "The general theory of the mechanical, electromagnetic and thermodynamic properties of black holes", in Hawking, S. W.; Israel, W., General Relativity, an Einstein Centenary Survey, Cambridge University Press, pp. 294–369 and 860–863, ISBN 978-0-521-29928-2
- Celotti, Annalisa; Miller, John C.; Sciama, Dennis W. (1999), "Astrophysical evidence for the existence of black holes", Class. Quantum Grav. 16 (12A): A3–A21, doi:10.1088/0264-9381/16/12A/301, Bibcode: 1999CQGra..16A...3C
- Chandrasekhar, Subrahmanyan (1983), The Mathematical Theory of Black Holes, New York: Oxford University Press, ISBN 978-0-19-850370-5
- Chandrasekhar, Subrahmanyan (1984), "The general theory of relativity – Why 'It is probably the most beautiful of all existing theories'", Journal of Astrophysics and Astronomy 5 (1): 3–11, doi:10.1007/BF02714967, Bibcode: 1984JApA....5....3C
- Charbonnel, C.; Primas, F. (2005), "The Lithium Content of the Galactic Halo Stars", Astronomy & Astrophysics 442 (3): 961–992, doi:10.1051/0004-6361:20042491, Bibcode: 2005A&A...442..961C
- Ciufolini, Ignazio; Pavlis, Erricos C. (2004), "A confirmation of the general relativistic prediction of the Lense–Thirring effect", Nature 431 (7011): 958–960, doi:10.1038/nature03007, PMID 15496915, Bibcode: 2004Natur.431..958C
- Ciufolini, Ignazio; Pavlis, Erricos C.; Peron, R. (2006), "Determination of frame-dragging using Earth gravity models from CHAMP and GRACE", New Astron. 11 (8): 527–550, doi:10.1016/j.newast.2006.02.001, Bibcode: 2006NewA...11..527C
- Coc, A.; Vangioni-Flam, Elisabeth; Descouvemont, Pierre; Adahchour, Abderrahim; Angulo, Carmen (2004), "Updated Big Bang Nucleosynthesis confronted to WMAP observations and to the Abundance of Light Elements", Astrophysical Journal 600 (2): 544–552, doi:10.1086/380121, Bibcode: 2004ApJ...600..544C
- Cutler, Curt; Thorne, Kip S. (2002), "An overview of gravitational wave sources", in Bishop, Nigel; Maharaj, Sunil D., Proceedings of 16th International Conference on General Relativity and Gravitation (GR16), World Scientific, p. 4090, ISBN 978-981-238-171-2, Bibcode: 2002gr.qc.....4090C
- Dalal, Neal; Holz, Daniel E.; Hughes, Scott A.; Jain, Bhuvnesh (2006), "Short GRB and binary black hole standard sirens as a probe of dark energy", Phys. Rev. D 74 (6): 063006, doi:10.1103/PhysRevD.74.063006, Bibcode: 2006PhRvD..74f3006D
- Danzmann, Karsten; Rüdiger, Albrecht (2003), "LISA Technology—Concepts, Status, Prospects", Class. Quantum Grav. 20 (10): S1–S9, doi:10.1088/0264-9381/20/10/301, Bibcode: 2003CQGra..20S...1D, http://www.srl.caltech.edu/lisa/documents/KarstenAlbrechtOverviewCQG20-2003.pdf
- Donoghue, John F. (1995), "Introduction to the Effective Field Theory Description of Gravity", in Cornet, Fernando, Effective Theories: Proceedings of the Advanced School, Almunecar, Spain, 26 June–1 July 1995, Singapore: World Scientific, p. 12024, ISBN 978-981-02-2908-5, Bibcode: 1995gr.qc....12024D
- Theory and Practice of Natural Computing: Fourth International Conference, TPNC 2015, Mieres, Spain, December 15–16, 2015. Proceedings. Springer. 2015. ISBN 978-3-319-26841-5. https://books.google.com/books?id=XmwiCwAAQBAJ.
- Duff, Michael (1996), "M-Theory (the Theory Formerly Known as Strings)", Int. J. Mod. Phys. A 11 (32): 5623–5641, doi:10.1142/S0217751X96002583, Bibcode: 1996IJMPA..11.5623D
- Ehlers, Jürgen (1973), "Survey of general relativity theory", in Israel, Werner, Relativity, Astrophysics and Cosmology, D. Reidel, pp. 1–125, ISBN 978-90-277-0369-9
- Ehlers, Jürgen; Falco, Emilio E.; Schneider, Peter (1992), Gravitational lenses, Springer, ISBN 978-3-540-66506-9
- Ehlers, Jürgen; Lämmerzahl, Claus, eds. (2006), Special Relativity—Will it Survive the Next 101 Years?, Springer, ISBN 978-3-540-34522-0
- Ehlers, Jürgen; Rindler, Wolfgang (1997), "Local and Global Light Bending in Einstein's and other Gravitational Theories", General Relativity and Gravitation 29 (4): 519–529, doi:10.1023/A:1018843001842, Bibcode: 1997GReGr..29..519E
- Einstein, Albert (1907), "Über das Relativitätsprinzip und die aus demselben gezogene Folgerungen", Jahrbuch der Radioaktivität und Elektronik 4: 411, https://einsteinpapers.press.princeton.edu/vol2-doc/468 See also English translation at Einstein Papers Project
- Einstein, Albert (1915), "Die Feldgleichungen der Gravitation", Sitzungsberichte der Preussischen Akademie der Wissenschaften zu Berlin: 844–847, https://einsteinpapers.press.princeton.edu/vol6-doc/272 See also English translation at Einstein Papers Project
- Einstein, Albert (1917), "Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie", Sitzungsberichte der Preußischen Akademie der Wissenschaften: 142, https://einsteinpapers.press.princeton.edu/vol6-doc/568 See also English translation at Einstein Papers Project
- Ellis, George F R; Van Elst, Henk (1999), "Cosmological Models", in Lachièze-Rey, Marc, Theoretical and Observational Cosmology, 541, pp. 1–116, doi:10.1007/978-94-011-4455-1_1, ISBN 978-0-7923-5946-3, Bibcode: 1999ASIC..541....1E
- Engler, Gideon (2002), "Einstein and the most beautiful theories in physics", International Studies in the Philosophy of Science 16 (1): 27–37, doi:10.1080/02698590120118800
- Everitt, C. W. F.; Buchman, S.; DeBra, D. B.; Keiser, G. M. (2001), "Gravity Probe B: Countdown to launch", in Lämmerzahl, C.; Everitt, C. W. F.; Hehl, F. W., Gyros, Clocks, and Interferometers: Testing Relativistic Gravity in Space (Lecture Notes in Physics 562), Springer, pp. 52–82, ISBN 978-3-540-41236-6
- Everitt, C. W. F.; Parkinson, Bradford; Kahn, Bob (2007), The Gravity Probe B experiment. Post Flight Analysis—Final Report (Preface and Executive Summary), Project Report: NASA, Stanford University and Lockheed Martin, http://einstein.stanford.edu/content/exec_summary/GP-B_ExecSum-scrn.pdf, retrieved 5 August 2007
- Falcke, Heino; Melia, Fulvio; Agol, Eric (2000), "Viewing the Shadow of the Black Hole at the Galactic Center", Astrophysical Journal 528 (1): L13–L16, doi:10.1086/312423, PMID 10587484, Bibcode: 2000ApJ...528L..13F
- Font, José A. (2003), "Numerical Hydrodynamics in General Relativity", Living Reviews in Relativity 6 (1): 4, doi:10.12942/lrr-2003-4, PMID 29104452, Bibcode: 2003LRR.....6....4F
- Fourès-Bruhat, Yvonne (1952), "Théoréme d'existence pour certains systémes d'équations aux derivées partielles non linéaires", Acta Mathematica 88 (1): 141–225, doi:10.1007/BF02392131, Bibcode: 1952AcMa...88..141F
- Frauendiener, Jörg (2004), "Conformal Infinity", Living Reviews in Relativity 7 (1): 1, doi:10.12942/lrr-2004-1, PMID 28179863, Bibcode: 2004LRR.....7....1F
- Friedrich, Helmut (2005), "Is general relativity 'essentially understood'?", Annalen der Physik 15 (1–2): 84–108, doi:10.1002/andp.200510173, Bibcode: 2006AnP...518...84F
- Futamase, T.; Itoh, Y. (2006), "The Post-Newtonian Approximation for Relativistic Compact Binaries", Living Reviews in Relativity 10 (1): 2, doi:10.12942/lrr-2007-2, PMID 28179819, Bibcode: 2007LRR....10....2F
- Gamow, George (1970), My World Line, Viking Press, ISBN 978-0-670-50376-6
- Garfinkle, David (2007), "Of singularities and breadmaking", Einstein Online (Max Planck Institute for Gravitational Physics), http://www.einstein-online.info/en/spotlights/singularities_bkl/index.html, retrieved 3 August 2007
- Geroch, Robert (1996). "Partial Differential Equations of Physics". General Relativity: 19. Bibcode: 1996gere.conf...19G.
- Giulini, Domenico (2005), Special Relativity: A First Encounter, Oxford University Press, ISBN 978-0-19-856746-2
- Giulini, Domenico (2006), "Algebraic and Geometric Structures in Special Relativity", in Ehlers, Jürgen; Lämmerzahl, Claus, Special Relativity—Will it Survive the Next 101 Years?, Lecture Notes in Physics, 702, pp. 45–111, doi:10.1007/3-540-34523-X_4, ISBN 978-3-540-34522-0, Bibcode: 2006math.ph...2018G
- Giulini, Domenico (2007), "Remarks on the Notions of General Covariance and Background Independence", in Stamatescu, I. O., Approaches to Fundamental Physics, Lecture Notes in Physics, 721, pp. 105–120, doi:10.1007/978-3-540-71117-9_6, ISBN 978-3-540-71115-5, Bibcode: 2007LNP...721..105G
- Gnedin, Nickolay Y. (2005), "Digitizing the Universe", Nature 435 (7042): 572–573, doi:10.1038/435572a, PMID 15931201, Bibcode: 2005Natur.435..572G
- Goenner, Hubert F. M. (2004), "On the History of Unified Field Theories", Living Reviews in Relativity 7 (1): 2, doi:10.12942/lrr-2004-2, PMID 28179864, Bibcode: 2004LRR.....7....2G
- Goroff, Marc H.; Sagnotti, Augusto (1985), "Quantum gravity at two loops", Phys. Lett. 160B (1–3): 81–86, doi:10.1016/0370-2693(85)91470-4, Bibcode: 1985PhLB..160...81G
- Gourgoulhon, Eric (2007). "3+1 Formalism and Bases of Numerical Relativity". arXiv:gr-qc/0703035.
- Gowdy, Robert H. (1971), "Gravitational Waves in Closed Universes", Phys. Rev. Lett. 27 (12): 826–829, doi:10.1103/PhysRevLett.27.826, Bibcode: 1971PhRvL..27..826G
- Gowdy, Robert H. (1974), "Vacuum spacetimes with two-parameter spacelike isometry groups and compact invariant hypersurfaces: Topologies and boundary conditions", Annals of Physics 83 (1): 203–241, doi:10.1016/0003-4916(74)90384-4, Bibcode: 1974AnPhy..83..203G
- Green, M. B.; Schwarz, J. H.; Witten, E. (1987), Superstring theory. Volume 1: Introduction, Cambridge University Press, ISBN 978-0-521-35752-4
- Greenstein, J. L.; Oke, J. B.; Shipman, H. L. (1971), "Effective Temperature, Radius, and Gravitational Redshift of Sirius B", Astrophysical Journal 169: 563, doi:10.1086/151174, Bibcode: 1971ApJ...169..563G
- Hamber, Herbert W. (2009), Hamber, Herbert W, ed., Quantum Gravitation – The Feynman Path Integral Approach, Springer Publishing, doi:10.1007/978-3-540-85293-3, ISBN 978-3-540-85292-6, https://cds.cern.ch/record/1233211
- Gödel, Kurt (1949). "An Example of a New Type of Cosmological Solution of Einstein's Field Equations of Gravitation". Rev. Mod. Phys. 21 (3): 447–450. doi:10.1103/RevModPhys.21.447. Bibcode: 1949RvMP...21..447G.
- Hafele, J. C.; Keating, R. E. (14 July 1972). "Around-the-World Atomic Clocks: Predicted Relativistic Time Gains". Science 177 (4044): 166–168. doi:10.1126/science.177.4044.166. PMID 17779917. Bibcode: 1972Sci...177..166H.
- Hafele, J. C.; Keating, R. E. (14 July 1972). "Around-the-World Atomic Clocks: Observed Relativistic Time Gains". Science 177 (4044): 168–170. doi:10.1126/science.177.4044.168. PMID 17779918. Bibcode: 1972Sci...177..168H.
- Havas, P. (1964), "Four-Dimensional Formulation of Newtonian Mechanics and Their Relation to the Special and the General Theory of Relativity", Rev. Mod. Phys. 36 (4): 938–965, doi:10.1103/RevModPhys.36.938, Bibcode: 1964RvMP...36..938H
- Hawking, Stephen W. (1966), "The occurrence of singularities in cosmology", Proceedings of the Royal Society A294 (1439): 511–521, doi:10.1098/rspa.1966.0221, Bibcode: 1966RSPSA.294..511H
- Hawking, S. W. (1975), "Particle Creation by Black Holes", Communications in Mathematical Physics 43 (3): 199–220, doi:10.1007/BF02345020, Bibcode: 1975CMaPh..43..199H, http://projecteuclid.org/euclid.cmp/1103899181
- Hawking, Stephen W. (1987), "Quantum cosmology", in Hawking, Stephen W.; Israel, Werner, 300 Years of Gravitation, Cambridge University Press, pp. 631–651, ISBN 978-0-521-37976-2
- Hawking, Stephen W.; Ellis, George F. R. (1973), The large scale structure of space-time, Cambridge University Press, ISBN 978-0-521-09906-6
- Heckmann, O. H. L.; Schücking, E. (1959), "Newtonsche und Einsteinsche Kosmologie", in Flügge, S., Encyclopedia of Physics, 53, p. 489
- Heusler, Markus (1998), "Stationary Black Holes: Uniqueness and Beyond", Living Reviews in Relativity 1 (1): 6, doi:10.12942/lrr-1998-6, PMID 28937184, Bibcode: 1998LRR.....1....6H
- Heusler, Markus (1996), Black Hole Uniqueness Theorems, Cambridge University Press, ISBN 978-0-521-56735-0
- Hey, Tony; Walters, Patrick (2003), The new quantum universe, Cambridge University Press, ISBN 978-0-521-56457-1, Bibcode: 2003nqu..book.....H
- Hough, Jim; Rowan, Sheila (2000), "Gravitational Wave Detection by Interferometry (Ground and Space)", Living Reviews in Relativity 3 (1): 3, doi:10.12942/lrr-2000-3, PMID 28179855, Bibcode: 2000LRR.....3....3R
- Hubble, Edwin (1929), "A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae", Proc. Natl. Acad. Sci. 15 (3): 168–173, doi:10.1073/pnas.15.3.168, PMID 16577160, Bibcode: 1929PNAS...15..168H
- Hulse, Russell A.; Taylor, Joseph H. (1975), "Discovery of a pulsar in a binary system", Astrophys. J. 195: L51–L55, doi:10.1086/181708, Bibcode: 1975ApJ...195L..51H
- Ibanez, L. E. (2000), "The second string (phenomenology) revolution", Class. Quantum Grav. 17 (5): 1117–1128, doi:10.1088/0264-9381/17/5/321, Bibcode: 2000CQGra..17.1117I
- Iorio, L. (2006), "A note on the evidence of the gravitomagnetic field of Mars", Classical and Quantum Gravity 23 (17): 5451–5454, doi:10.1088/0264-9381/23/17/N01, Bibcode: 2006CQGra..23.5451I
- Iorio, L. (2009), "An Assessment of the Systematic Uncertainty in Present and Future Tests of the Lense–Thirring Effect with Satellite Laser Ranging", Space Sci. Rev. 148 (1–4): 363–381, doi:10.1007/s11214-008-9478-1, Bibcode: 2009SSRv..148..363I
- Iorio, L. (2010), "On the Lense–Thirring test with the Mars Global Surveyor in the gravitational field of Mars", Central European Journal of Physics 8 (3): 509–513, doi:10.2478/s11534-009-0117-6, Bibcode: 2010CEJPh...8..509I
- Isham, Christopher J. (1994), "Prima facie questions in quantum gravity", in Ehlers, Jürgen; Friedrich, Helmut, Canonical Gravity: From Classical to Quantum, Springer, ISBN 978-3-540-58339-4
- Israel, Werner (1971), "Event Horizons and Gravitational Collapse", General Relativity and Gravitation 2 (1): 53–59, doi:10.1007/BF02450518, Bibcode: 1971GReGr...2...53I
- Israel, Werner (1987), "Dark stars: the evolution of an idea", in Hawking, Stephen W.; Israel, Werner, 300 Years of Gravitation, Cambridge University Press, pp. 199–276, ISBN 978-0-521-37976-2
- Janssen, Michel (2005), "Of pots and holes: Einstein's bumpy road to general relativity" (PDF), Annalen der Physik 14 (S1): 58–85, doi:10.1002/andp.200410130, Bibcode: 2005AnP...517S..58J, https://netfiles.umn.edu/xythoswfs/webui/_xy-15267453_1-t_ycAqaW0A, retrieved 28 August 2010
- Jaranowski, Piotr; Królak, Andrzej (2005), "Gravitational-Wave Data Analysis. Formalism and Sample Applications: The Gaussian Case", Living Reviews in Relativity 8 (1): 3, doi:10.12942/lrr-2005-3, PMID 28163647, Bibcode: 2005LRR.....8....3J
- Kahn, Bob (1996–2012), Gravity Probe B Website, Stanford University, http://einstein.stanford.edu/, retrieved 20 April 2012
- Kahn, Bob (14 April 2007), Was Einstein right? Scientists provide first public peek at Gravity Probe B results (Stanford University Press Release), Stanford University News Service, http://einstein.stanford.edu/content/press_releases/SU/pr-aps-041807.pdf
- Kamionkowski, Marc; Kosowsky, Arthur; Stebbins, Albert (1997), "Statistics of Cosmic Microwave Background Polarization", Phys. Rev. D55 (12): 7368–7388, doi:10.1103/PhysRevD.55.7368, Bibcode: 1997PhRvD..55.7368K
- Kennefick, Daniel (2005), "Astronomers Test General Relativity: Light-bending and the Solar Redshift", in Renn, Jürgen, One hundred authors for Einstein, Wiley-VCH, pp. 178–181, ISBN 978-3-527-40574-9
- Kennefick, Daniel (2007), "Not Only Because of Theory: Dyson, Eddington and the Competing Myths of the 1919 Eclipse Expedition", Proceedings of the 7th Conference on the History of General Relativity, Tenerife, 2005, 0709, p. 685, doi:10.1016/j.shpsa.2012.07.010, Bibcode: 2007arXiv0709.0685K
- Kenyon, I. R. (1990), General Relativity, Oxford University Press, ISBN 978-0-19-851996-6
- Kochanek, C.S.; Falco, E.E.; Impey, C.; Lehar, J. (2007), CASTLES Survey Website, Harvard-Smithsonian Center for Astrophysics, http://cfa-www.harvard.edu/castles, retrieved 21 August 2007
- Komar, Arthur (1959), "Covariant Conservation Laws in General Relativity", Phys. Rev. 113 (3): 934–936, doi:10.1103/PhysRev.113.934, Bibcode: 1959PhRv..113..934K
- Kramer, Michael (2004). "Millisecond Pulsarsas Tools of Fundamental Physics". in Karshenboim, S. G.; Peik, E.. Astrophysics, Clocks and Fundamental Constants. Lecture Notes in Physics. 648. pp. 33–54. doi:10.1007/978-3-540-40991-5_3. ISBN 978-3-540-21967-5. Bibcode: 2004LNP...648...33K.
- Kramer, M.; Stairs, I. H.; Manchester, R. N.; McLaughlin, M. A.; Lyne, A. G.; Ferdman, R. D.; Burgay, M.; Lorimer, D. R. et al. (2006), "Tests of general relativity from timing the double pulsar", Science 314 (5796): 97–102, doi:10.1126/science.1132305, PMID 16973838, Bibcode: 2006Sci...314...97K
- Kraus, Ute (1998), "Light Deflection Near Neutron Stars", Relativistic Astrophysics, Vieweg, pp. 66–81, ISBN 978-3-528-06909-4
- Kuchař, Karel (1973), "Canonical Quantization of Gravity", in Israel, Werner, Relativity, Astrophysics and Cosmology, D. Reidel, pp. 237–288, ISBN 978-90-277-0369-9
- Künzle, H. P. (1972), "Galilei and Lorentz Structures on spacetime: comparison of the corresponding geometry and physics", Annales de l'Institut Henri Poincaré A 17: 337–362, http://www.numdam.org/item?id=AIHPA_1972__17_4_337_0
- Lahav, Ofer; Suto, Yasushi (2004), "Measuring our Universe from Galaxy Redshift Surveys", Living Reviews in Relativity 7 (1): 8, doi:10.12942/lrr-2004-8, PMID 28163643, Bibcode: 2004LRR.....7....8L
- Landau, L. D.; Lifshitz, E. M. (1975), The Classical Theory of Fields, v. 2, Elsevier Science, Ltd., ISBN 978-0-08-018176-9
- Lehner, Luis (2001), "Numerical Relativity: A review", Class. Quantum Grav. 18 (17): R25–R86, doi:10.1088/0264-9381/18/17/202, Bibcode: 2001CQGra..18R..25L
- Lehner, Luis (2002). "General Relativity and Gravitation". General Relativity and Gravitation: Proceedings of the 16th International Conference, Durban, South Africa, 15–21 July 2001. p. 210. doi:10.1142/9789812776556_0010. ISBN 978-981-238-171-2. Bibcode: 2002grg..conf..210L.
- Linde, Andrei (2005), "Particle Physics and Inflationary Cosmology", Contemp.concepts Phys 5: 1–362, ISBN 978-3-7186-0489-0, Bibcode: 2005hep.th....3203L
- Linde, Andrei (2006), "Towards inflation in string theory", J. Phys. Conf. Ser. 24 (1): 151–160, doi:10.1088/1742-6596/24/1/018, Bibcode: 2005JPhCS..24..151L
- Loll, Renate (1998), "Discrete Approaches to Quantum Gravity in Four Dimensions", Living Reviews in Relativity 1 (1): 13, doi:10.12942/lrr-1998-13, PMID 28191826, Bibcode: 1998LRR.....1...13L
- Lovelock, David (1972), "The Four-Dimensionality of Space and the Einstein Tensor", J. Math. Phys. 13 (6): 874–876, doi:10.1063/1.1666069, Bibcode: 1972JMP....13..874L
- MacCallum, M. (2006), "Finding and using exact solutions of the Einstein equations", in Mornas, L.; Alonso, J. D., AIP Conference Proceedings, 841, pp. 129–143, doi:10.1063/1.2218172, Bibcode: 2006AIPC..841..129M
- Maddox, John (1998), What Remains To Be Discovered, Macmillan, ISBN 978-0-684-82292-1, https://archive.org/details/whatremainstobed00madd
- Mannheim, Philip D. (2006), "Alternatives to Dark Matter and Dark Energy", Prog. Part. Nucl. Phys. 56 (2): 340–445, doi:10.1016/j.ppnp.2005.08.001, Bibcode: 2006PrPNP..56..340M
- Mather, J. C.; Cheng, E. S.; Cottingham, D. A.; Eplee, R. E.; Fixsen, D. J.; Hewagama, T.; Isaacman, R. B.; Jensen, K. A. et al. (1994), "Measurement of the cosmic microwave spectrum by the COBE FIRAS instrument", Astrophysical Journal 420: 439–444, doi:10.1086/173574, Bibcode: 1994ApJ...420..439M
- Mermin, N. David (2005), It's About Time. Understanding Einstein's Relativity, Princeton University Press, ISBN 978-0-691-12201-4, https://archive.org/details/itsabouttimeunde0000merm
- Messiah, Albert (1999), Quantum Mechanics, Dover Publications, ISBN 978-0-486-40924-5
- Miller, Cole (2002), Stellar Structure and Evolution (Lecture notes for Astronomy 606), University of Maryland, http://www.astro.umd.edu/~miller/teaching/astr606/, retrieved 25 July 2007
- Misner, Charles W.; Thorne, Kip. S.; Wheeler, John A. (1973), Gravitation, W. H. Freeman, ISBN 978-0-7167-0344-0
- Narayan, Ramesh (2006), "Black holes in astrophysics", New Journal of Physics 7 (1): 199, doi:10.1088/1367-2630/7/1/199, Bibcode: 2005NJPh....7..199N
- Narayan, Ramesh; Bartelmann, Matthias (1997). "Lectures on Gravitational Lensing". arXiv:astro-ph/9606001.
- Narlikar, Jayant V. (1993), Introduction to Cosmology, Cambridge University Press, ISBN 978-0-521-41250-6
- Nordström, Gunnar (1918), "On the Energy of the Gravitational Field in Einstein's Theory", Verhandl. Koninkl. Ned. Akad. Wetenschap. 26: 1238–1245, Bibcode: 1918KNAB...20.1238N
- Nordtvedt, Kenneth (2003). "Lunar Laser Ranging—a comprehensive probe of post-Newtonian gravity". arXiv:gr-qc/0301024.
- Norton, John D. (1985), "What was Einstein's principle of equivalence?", Studies in History and Philosophy of Science 16 (3): 203–246, doi:10.1016/0039-3681(85)90002-0, Bibcode: 1985SHPSA..16..203N, http://www.pitt.edu/~jdnorton/papers/ProfE_re-set.pdf, retrieved 11 June 2007
- Ohanian, Hans C.; Ruffini, Remo (1994), Gravitation and Spacetime, W. W. Norton & Company, ISBN 978-0-393-96501-8
- Olive, K. A.; Skillman, E. A. (2004), "A Realistic Determination of the Error on the Primordial Helium Abundance", Astrophysical Journal 617 (1): 29–49, doi:10.1086/425170, Bibcode: 2004ApJ...617...29O
- O'Meara, John M.; Tytler, David; Kirkman, David; Suzuki, Nao; Prochaska, Jason X.; Lubin, Dan; Wolfe, Arthur M. (2001), "The Deuterium to Hydrogen Abundance Ratio Towards a Fourth QSO: HS0105+1619", Astrophysical Journal 552 (2): 718–730, doi:10.1086/320579, Bibcode: 2001ApJ...552..718O
- Oppenheimer, J. Robert; Snyder, H. (1939), "On continued gravitational contraction", Physical Review 56 (5): 455–459, doi:10.1103/PhysRev.56.455, Bibcode: 1939PhRv...56..455O
- Overbye, Dennis (1999), Lonely Hearts of the Cosmos: the story of the scientific quest for the secret of the Universe, Back Bay, ISBN 978-0-316-64896-7
- Pais, Abraham (1982), 'Subtle is the Lord ...' The Science and life of Albert Einstein, Oxford University Press, ISBN 978-0-19-853907-0, https://archive.org/details/subtleislordscie00pais
- Peacock, John A. (1999), Cosmological Physics, Cambridge University Press, ISBN 978-0-521-41072-4
- Peebles, P. J. E. (1966), "Primordial Helium abundance and primordial fireball II", Astrophysical Journal 146: 542–552, doi:10.1086/148918, Bibcode: 1966ApJ...146..542P
- Peebles, P. J. E. (1993), Principles of physical cosmology, Princeton University Press, ISBN 978-0-691-01933-8, https://archive.org/details/principlesofphys00pjep
- Peebles, P.J.E.; Schramm, D.N.; Turner, E.L.; Kron, R.G. (1991), "The case for the relativistic hot Big Bang cosmology", Nature 352 (6338): 769–776, doi:10.1038/352769a0, Bibcode: 1991Natur.352..769P
- Penrose, Roger (1965), "Gravitational collapse and spacetime singularities", Physical Review Letters 14 (3): 57–59, doi:10.1103/PhysRevLett.14.57, Bibcode: 1965PhRvL..14...57P
- Penrose, Roger (1969), "Gravitational collapse: the role of general relativity", Rivista del Nuovo Cimento 1: 252–276, Bibcode: 1969NCimR...1..252P
- Penrose, Roger (2004), The Road to Reality, A. A. Knopf, ISBN 978-0-679-45443-4, https://archive.org/details/roadtorealitycom00penr_0
- Penzias, A. A.; Wilson, R. W. (1965), "A measurement of excess antenna temperature at 4080 Mc/s", Astrophysical Journal 142: 419–421, doi:10.1086/148307, Bibcode: 1965ApJ...142..419P
- Peskin, Michael E.; Schroeder, Daniel V. (1995), An Introduction to Quantum Field Theory, Addison-Wesley, ISBN 978-0-201-50397-5, https://archive.org/details/introductiontoqu0000pesk
- Peskin, Michael E. (2007), "Dark Matter and Particle Physics", Journal of the Physical Society of Japan 76 (11): 111017, doi:10.1143/JPSJ.76.111017, Bibcode: 2007JPSJ...76k1017P
- Poincaré, M. H. (1905), "Sur la dynamique de l'électron", Comptes rendus hebdomadaires des séances de l'Académie des sciences 140: 1504-1508
- Poisson, Eric (27 May 2004a). "The Motion of Point Particles in Curved Spacetime". Living Reviews in Relativity 7 (1): 6. doi:10.12942/lrr-2004-6. PMID 28179866. Bibcode: 2004LRR.....7....6P.
- Poisson, Eric (2004), A Relativist's Toolkit. The Mathematics of Black-Hole Mechanics, Cambridge University Press, ISBN 978-0-521-83091-1, Bibcode: 2004rtmb.book.....P
- Polchinski, Joseph (1998a), String Theory Vol. I: An Introduction to the Bosonic String, Cambridge University Press, ISBN 978-0-521-63303-1
- Polchinski, Joseph (1998b), String Theory Vol. II: Superstring Theory and Beyond, Cambridge University Press, ISBN 978-0-521-63304-8
- Pound, R. V.; Rebka, G. A. (1959), "Gravitational Red-Shift in Nuclear Resonance", Physical Review Letters 3 (9): 439–441, doi:10.1103/PhysRevLett.3.439, Bibcode: 1959PhRvL...3..439P
- Pound, R. V.; Rebka, G. A. (1960), "Apparent weight of photons", Phys. Rev. Lett. 4 (7): 337–341, doi:10.1103/PhysRevLett.4.337, Bibcode: 1960PhRvL...4..337P
- Pound, R. V.; Snider, J. L. (1964), "Effect of Gravity on Nuclear Resonance", Phys. Rev. Lett. 13 (18): 539–540, doi:10.1103/PhysRevLett.13.539, Bibcode: 1964PhRvL..13..539P
- Ramond, Pierre (1990), Field Theory: A Modern Primer, Addison-Wesley, ISBN 978-0-201-54611-8
- Rees, Martin (1966), "Appearance of Relativistically Expanding Radio Sources", Nature 211 (5048): 468–470, doi:10.1038/211468a0, Bibcode: 1966Natur.211..468R
- Reissner, H. (1916), "Über die Eigengravitation des elektrischen Feldes nach der Einsteinschen Theorie", Annalen der Physik 355 (9): 106–120, doi:10.1002/andp.19163550905, Bibcode: 1916AnP...355..106R, https://zenodo.org/record/1447315
- Remillard, Ronald A.; Lin, Dacheng; Cooper, Randall L.; Narayan, Ramesh (2006), "The Rates of Type I X-Ray Bursts from Transients Observed with RXTE: Evidence for Black Hole Event Horizons", Astrophysical Journal 646 (1): 407–419, doi:10.1086/504862, Bibcode: 2006ApJ...646..407R
- Renn, Jürgen, ed. (2007), The Genesis of General Relativity (4 Volumes), Dordrecht: Springer, ISBN 978-1-4020-3999-7
- Renn, Jürgen, ed. (2005), Albert Einstein—Chief Engineer of the Universe: Einstein's Life and Work in Context, Berlin: Wiley-VCH, ISBN 978-3-527-40571-8
- Reula, Oscar A. (1998), "Hyperbolic Methods for Einstein's Equations", Living Reviews in Relativity 1 (1): 3, doi:10.12942/lrr-1998-3, PMID 28191833, Bibcode: 1998LRR.....1....3R
- Rindler, Wolfgang (2001), Relativity. Special, General and Cosmological, Oxford University Press, ISBN 978-0-19-850836-6
- Rindler, Wolfgang (1991), Introduction to Special Relativity, Clarendon Press, Oxford, ISBN 978-0-19-853952-0, https://archive.org/details/introductiontosp0000rind
- Robson, Ian (1996), Active galactic nuclei, John Wiley, ISBN 978-0-471-95853-6
- Roulet, E.; Mollerach, S. (1997), "Microlensing", Physics Reports 279 (2): 67–118, doi:10.1016/S0370-1573(96)00020-8, Bibcode: 1997PhR...279...67R
- Rovelli, Carlo, ed. (2015), General Relativity: The most beautiful of theories (de Gruyter Studies in Mathematical Physics), Boston: Walter de Gruyter GmbH, ISBN 978-3-11-034042-6
- Rovelli, Carlo (2000). "Notes for a brief history of quantum gravity". arXiv:gr-qc/0006061.
- Rovelli, Carlo (1998), "Loop Quantum Gravity", Living Reviews in Relativity 1 (1): 1, doi:10.12942/lrr-1998-1, PMID 28937180, Bibcode: 1998LRR.....1....1R
- Schäfer, Gerhard (2004), "Gravitomagnetic Effects", General Relativity and Gravitation 36 (10): 2223–2235, doi:10.1023/B:GERG.0000046180.97877.32, Bibcode: 2004GReGr..36.2223S
- Schödel, R.; Ott, T.; Genzel, R.; Eckart, A.; Mouawad, N.; Alexander, T. (2003), "Stellar Dynamics in the Central Arcsecond of Our Galaxy", Astrophysical Journal 596 (2): 1015–1034, doi:10.1086/378122, Bibcode: 2003ApJ...596.1015S
- Schutz, Bernard F. (1985), A first course in general relativity, Cambridge University Press, ISBN 978-0-521-27703-7
- Schutz, Bernard F. (2003), Gravity from the ground up, Cambridge University Press, ISBN 978-0-521-45506-0
- Schwarz, John H. (2007), "String Theory: Progress and Problems", Progress of Theoretical Physics Supplement 170: 214–226, doi:10.1143/PTPS.170.214, Bibcode: 2007PThPS.170..214S
- Schwarzschild, Karl (1916a), "Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie", Sitzungsber. Preuss. Akad. D. Wiss.: 189–196, Bibcode: 1916SPAW.......189S
- Schwarzschild, Karl (1916b), "Über das Gravitationsfeld einer Kugel aus inkompressibler Flüssigkeit nach der Einsteinschen Theorie", Sitzungsber. Preuss. Akad. D. Wiss.: 424–434, Bibcode: 1916skpa.conf..424S
- Seidel, Edward (1998), "Numerical Relativity: Towards Simulations of 3D Black Hole Coalescence", in Narlikar, J. V.; Dadhich, N., Gravitation and Relativity: At the turn of the millennium (Proceedings of the GR-15 Conference, held at IUCAA, Pune, India, December 16–21, 1997), IUCAA, p. 6088, ISBN 978-81-900378-3-9, Bibcode: 1998gr.qc.....6088S
- Seljak, Uros̆; Zaldarriaga, Matias (1997), "Signature of Gravity Waves in the Polarization of the Microwave Background", Phys. Rev. Lett. 78 (11): 2054–2057, doi:10.1103/PhysRevLett.78.2054, Bibcode: 1997PhRvL..78.2054S
- Shapiro, S. S.; Davis, J. L.; Lebach, D. E.; Gregory, J. S. (2004), "Measurement of the solar gravitational deflection of radio waves using geodetic very-long-baseline interferometry data, 1979–1999", Phys. Rev. Lett. 92 (12): 121101, doi:10.1103/PhysRevLett.92.121101, PMID 15089661, Bibcode: 2004PhRvL..92l1101S
- Shapiro, Irwin I. (1964), "Fourth test of general relativity", Phys. Rev. Lett. 13 (26): 789–791, doi:10.1103/PhysRevLett.13.789, Bibcode: 1964PhRvL..13..789S
- Singh, Simon (2004), Big Bang: The Origin of the Universe, Fourth Estate, ISBN 978-0-00-715251-3, Bibcode: 2004biba.book.....S
- Sorkin, Rafael D. (2005), "Causal Sets: Discrete Gravity", in Gomberoff, Andres; Marolf, Donald, Lectures on Quantum Gravity, Springer, p. 9009, ISBN 978-0-387-23995-8, Bibcode: 2003gr.qc.....9009S
- Sorkin, Rafael D. (1997), "Forks in the Road, on the Way to Quantum Gravity", Int. J. Theor. Phys. 36 (12): 2759–2781, doi:10.1007/BF02435709, Bibcode: 1997IJTP...36.2759S
- Spergel, D. N.; Verde, L.; Peiris, H. V.; Komatsu, E.; Nolta, M. R.; Bennett, C. L.; Halpern, M.; Hinshaw, G. et al. (2003), "First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters", Astrophys. J. Suppl. Ser. 148 (1): 175–194, doi:10.1086/377226, Bibcode: 2003ApJS..148..175S
- Spergel, D. N. (2007), "Wilkinson Microwave Anisotropy Probe (WMAP) Three Year Results: Implications for Cosmology", Astrophysical Journal Supplement 170 (2): 377–408, doi:10.1086/513700, Bibcode: 2007ApJS..170..377S
- Springel, Volker; White, Simon D. M.; Jenkins, Adrian; Frenk, Carlos S.; Yoshida, Naoki; Gao, Liang; Navarro, Julio; Thacker, Robert et al. (2005), "Simulations of the formation, evolution and clustering of galaxies and quasars", Nature 435 (7042): 629–636, doi:10.1038/nature03597, PMID 15931216, Bibcode: 2005Natur.435..629S
- Stairs, Ingrid H. (2003), "Testing General Relativity with Pulsar Timing", Living Reviews in Relativity 6 (1): 5, doi:10.12942/lrr-2003-5, PMID 28163640, Bibcode: 2003LRR.....6....5S
- Stephani, H.; Kramer, D.; MacCallum, M.; Hoenselaers, C.; Herlt, E. (2003), Exact Solutions of Einstein's Field Equations (2 ed.), Cambridge University Press, ISBN 978-0-521-46136-8
- Synge, J. L. (1972), Relativity: The Special Theory, North-Holland Publishing Company, ISBN 978-0-7204-0064-9
- Szabados, László B. (2004), "Quasi-Local Energy–Momentum and Angular Momentum in GR", Living Reviews in Relativity 7 (1): 4, doi:10.12942/lrr-2004-4, PMID 28179865, Bibcode: 2004LRR.....7....4S
- Taylor, Joseph H. (1994), "Binary pulsars and relativistic gravity", Rev. Mod. Phys. 66 (3): 711–719, doi:10.1103/RevModPhys.66.711, Bibcode: 1994RvMP...66..711T, https://cds.cern.ch/record/1974220
- Thiemann, Thomas (2007), "Loop Quantum Gravity: An Inside View", Approaches to Fundamental Physics, Lecture Notes in Physics, 721, pp. 185–263, doi:10.1007/978-3-540-71117-9_10, ISBN 978-3-540-71115-5, Bibcode: 2007LNP...721..185T
- Thiemann, Thomas (2003). "Lectures on Loop Quantum Gravity". Quantum Gravity: From Theory to Experimental Search. Lecture Notes in Physics. 631. pp. 41–135. doi:10.1007/978-3-540-45230-0_3. ISBN 978-3-540-40810-9. Bibcode: 2003LNP...631...41T.
- 't Hooft, Gerard; Veltman, Martinus (1974), "One Loop Divergencies in the Theory of Gravitation", Annales de l'Institut Henri Poincaré A 20 (1): 69, Bibcode: 1974AIHPA..20...69T
- Thorne, Kip S. (1972), "Nonspherical Gravitational Collapse—A Short Review", in Klauder, J., Magic without Magic, W. H. Freeman, pp. 231–258
- Thorne, Kip S. (1994), Black Holes and Time Warps: Einstein's Outrageous Legacy, W W Norton & Company, ISBN 978-0-393-31276-8
- Thorne, Kip S. (1995), "Gravitational radiation", Particle and Nuclear Astrophysics and Cosmology in the Next Millennium: 160, ISBN 978-0-521-36853-7, Bibcode: 1995pnac.conf..160T
- Thorne, Kip (2003). "Warping spacetime". The future of theoretical physics and cosmology: celebrating Stephen Hawking's 60th birthday. Cambridge University Press. ISBN 978-0-521-82081-3. https://books.google.com/books?id=yLy4b61rfPwC.
- Townsend, Paul K. (1997). "Black Holes (Lecture notes)". arXiv:gr-qc/9707012.
- Townsend, Paul K. (1996). "Four Lectures on M-Theory". High Energy Physics and Cosmology 13: 385. Bibcode: 1997hepcbconf..385T.
- Traschen (2000), Bytsenko, A.; Williams, F., eds., "An Introduction to Black Hole Evaporation", Mathematical Methods of Physics (Proceedings of the 1999 Londrina Winter School) (World Scientific): 180, Bibcode: 2000mmp..conf..180T
- Trautman, Andrzej (2006), "Einstein–Cartan theory", in Françoise, J.-P.; Naber, G. L.; Tsou, S. T., Encyclopedia of Mathematical Physics, Vol. 2, Elsevier, pp. 189–195, Bibcode: 2006gr.qc.....6062T
- Unruh, W. G. (1976), "Notes on Black Hole Evaporation", Phys. Rev. D 14 (4): 870–892, doi:10.1103/PhysRevD.14.870, Bibcode: 1976PhRvD..14..870U
- Veltman, Martinus (1975), "Quantum Theory of Gravitation", in Balian, Roger; Zinn-Justin, Jean, Methods in Field Theory – Les Houches Summer School in Theoretical Physics., 77, North Holland
- Wald, Robert M. (1975), "On Particle Creation by Black Holes", Commun. Math. Phys. 45 (3): 9–34, doi:10.1007/BF01609863, Bibcode: 1975CMaPh..45....9W, http://projecteuclid.org/euclid.cmp/1103899393
- Wald, Robert M. (1984), General Relativity, University of Chicago Press, ISBN 978-0-226-87033-5
- Wald, Robert M. (1994), Quantum field theory in curved spacetime and black hole thermodynamics, University of Chicago Press, ISBN 978-0-226-87027-4, Bibcode: 1994qftc.book.....W
- Wald, Robert M. (2001), "The Thermodynamics of Black Holes", Living Reviews in Relativity 4 (1): 6, doi:10.12942/lrr-2001-6, PMID 28163633, Bibcode: 2001LRR.....4....6W
- Walsh, D.; Carswell, R. F.; Weymann, R. J. (1979), "0957 + 561 A, B: twin quasistellar objects or gravitational lens?", Nature 279 (5712): 381–4, doi:10.1038/279381a0, PMID 16068158, Bibcode: 1979Natur.279..381W
- Wambsganss, Joachim (1998), "Gravitational Lensing in Astronomy", Living Reviews in Relativity 1 (1): 12, doi:10.12942/lrr-1998-12, PMID 28937183, Bibcode: 1998LRR.....1...12W
- Weinberg, Steven (1972), Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity, John Wiley, ISBN 978-0-471-92567-5, https://archive.org/details/gravitationcosmo00stev_0
- Weinberg, Steven (1995), The Quantum Theory of Fields I: Foundations, Cambridge University Press, ISBN 978-0-521-55001-7, https://archive.org/details/quantumtheoryoff00stev
- Weinberg, Steven (1996), The Quantum Theory of Fields II: Modern Applications, Cambridge University Press, ISBN 978-0-521-55002-4, https://archive.org/details/quantumtheoryoff00stev
- Weinberg, Steven (2000), The Quantum Theory of Fields III: Supersymmetry, Cambridge University Press, ISBN 978-0-521-66000-6, https://archive.org/details/quantumtheoryoff00stev
- Weisberg, Joel M.; Taylor, Joseph H. (2003), "The Relativistic Binary Pulsar B1913+16"", in Bailes, M.; Nice, D. J.; Thorsett, S. E., Proceedings of "Radio Pulsars," Chania, Crete, August, 2002, ASP Conference Series
- Weiss, Achim (2006), "Elements of the past: Big Bang Nucleosynthesis and observation", Einstein Online (Max Planck Institute for Gravitational Physics), http://www.einstein-online.info/en/spotlights/BBN_obs/index.html, retrieved 24 February 2007
- Wheeler, John A. (1990), A Journey Into Gravity and Spacetime, Scientific American Library, San Francisco: W. H. Freeman, ISBN 978-0-7167-6034-4
- Will, Clifford M. (1993), Theory and experiment in gravitational physics, Cambridge University Press, ISBN 978-0-521-43973-2
- Will, Clifford M. (2006), "The Confrontation between General Relativity and Experiment", Living Reviews in Relativity 9 (1): 3, doi:10.12942/lrr-2006-3, PMID 28179873, Bibcode: 2006LRR.....9....3W
- Zwiebach, Barton (2004), A First Course in String Theory, Cambridge University Press, ISBN 978-0-521-83143-7
Further reading
Popular books
- Einstein, A. (1916), Relativity: The Special and the General Theory, Berlin, ISBN 978-3-528-06059-6
- Geroch, R. (1981), General Relativity from A to B, Chicago: University of Chicago Press, ISBN 978-0-226-28864-2
- Lieber, Lillian (2008), The Einstein Theory of Relativity: A Trip to the Fourth Dimension, Philadelphia: Paul Dry Books, Inc., ISBN 978-1-58988-044-3
- Schutz, Bernard F. (2001), "Gravitational radiation", in Murdin, Paul, Encyclopedia of Astronomy and Astrophysics, ISBN 978-1-56159-268-5
- Thorne, Kip; Hawking, Stephen (1994). Black Holes and Time Warps: Einstein's Outrageous Legacy. New York: W. W. Norton. ISBN 0-393-03505-0.
- Wald, Robert M. (1992), Space, Time, and Gravity: the Theory of the Big Bang and Black Holes, Chicago: University of Chicago Press, ISBN 978-0-226-87029-8
- Wheeler, John; Ford, Kenneth (1998), Geons, Black Holes, & Quantum Foam: a life in physics, New York: W. W. Norton, ISBN 978-0-393-31991-0
Beginning undergraduate textbooks
- Callahan, James J. (2000), The Geometry of Spacetime: an Introduction to Special and General Relativity, New York: Springer, ISBN 978-0-387-98641-8
- Taylor, Edwin F.; Wheeler, John Archibald (2000), Exploring Black Holes: Introduction to General Relativity, Addison Wesley, ISBN 978-0-201-38423-9
Advanced undergraduate textbooks
- Cheng, Ta-Pei (2005), Relativity, Gravitation and Cosmology: a Basic Introduction, Oxford and New York: Oxford University Press, ISBN 978-0-19-852957-6
- Dirac, Paul (1996), General Theory of Relativity, Princeton University Press, ISBN 978-0-691-01146-2
- Gron, O.; Hervik, S. (2007), Einstein's General theory of Relativity, Springer, ISBN 978-0-387-69199-2
- Hartle, James B. (2003), Gravity: an Introduction to Einstein's General Relativity, San Francisco: Addison-Wesley, ISBN 978-0-8053-8662-2
- Hughston, L. P.; Tod, K. P. (1991), Introduction to General Relativity, Cambridge: Cambridge University Press, ISBN 978-0-521-33943-8
- d'Inverno, Ray (1992), Introducing Einstein's Relativity, Oxford: Oxford University Press, ISBN 978-0-19-859686-8, https://archive.org/details/introducingeinst0000dinv
- Ludyk, Günter (2013). Einstein in Matrix Form (1st ed.). Berlin: Springer. ISBN 978-3-642-35797-8.
- Møller, Christian (1955), The Theory of Relativity, Oxford University Press, OCLC 7644624, https://archive.org/details/theoryofrelativi029229mbp
- Schutz, B. F. (2009), A First Course in General Relativity (Second ed.), Cambridge University Press, ISBN 978-0-521-88705-2, https://archive.org/details/firstcourseingen00bern_0
Graduate textbooks
- Carroll, Sean M. (2004), Spacetime and Geometry: An Introduction to General Relativity, San Francisco: Addison-Wesley, ISBN 978-0-8053-8732-2
- Grøn, Øyvind; Hervik, Sigbjørn (2007), Einstein's General Theory of Relativity, New York: Springer, ISBN 978-0-387-69199-2
- Landau, Lev D.; Lifshitz, Evgeny F. (1980), The Classical Theory of Fields (4th ed.), London: Butterworth-Heinemann, ISBN 978-0-7506-2768-9
- Stephani, Hans (1990), General Relativity: An Introduction to the Theory of the Gravitational Field, Cambridge: Cambridge University Press, ISBN 978-0-521-37941-0
- Will, Clifford; Poisson, Eric (2014). Gravity: Newtonian, Post-Newtonian, Relativistic. Cambridge University Press. ISBN 978-1-107-03286-6.
- Charles W. Misner; Kip S. Thorne; John Archibald Wheeler (1973), Gravitation, W. H. Freeman, Princeton University Press, ISBN 0-7167-0344-0
- R.K. Sachs; H. Wu (1977), General Relativity for Mathematicians, Springer-Verlag, ISBN 1461299055
- Wald, Robert M. (1984). General Relativity. Chicago: University of Chicago Press. ISBN 0-226-87032-4. OCLC 10018614.
Specialists' books
- Hawking, Stephen; Ellis, George (1975). The Large Scale Structure of Space-time. Cambridge University Press. ISBN 978-0-521-09906-6.
- Poisson, Eric (2007). A Relativist's Toolkit: The Mathematics of Black-Hole Mechanics. Cambridge University Press. ISBN 978-0-521-53780-3.
Journal articles
- Einstein, Albert (1916), "Die Grundlage der allgemeinen Relativitätstheorie", Annalen der Physik 49 (7): 769–822, doi:10.1002/andp.19163540702, Bibcode: 1916AnP...354..769E, https://einsteinpapers.press.princeton.edu/vol6-doc/311 See also English translation at Einstein Papers Project
- Flanagan, Éanna É.; Hughes, Scott A. (2005), "The basics of gravitational wave theory", New J. Phys. 7 (1): 204, doi:10.1088/1367-2630/7/1/204, Bibcode: 2005NJPh....7..204F
- Landgraf, M.; Hechler, M.; Kemble, S. (2005), "Mission design for LISA Pathfinder", Class. Quantum Grav. 22 (10): S487–S492, doi:10.1088/0264-9381/22/10/048, Bibcode: 2005CQGra..22S.487L
- Nieto, Michael Martin (2006), "The quest to understand the Pioneer anomaly", Europhysics News 37 (6): 30–34, doi:10.1051/epn:2006604, Bibcode: 2006ENews..37f..30N, http://www.europhysicsnews.org/articles/epn/pdf/2006/06/epn06604.pdf
- Shapiro, I. I.; Pettengill, Gordon; Ash, Michael; Stone, Melvin; Smith, William; Ingalls, Richard; Brockelman, Richard (1968), "Fourth test of general relativity: preliminary results", Phys. Rev. Lett. 20 (22): 1265–1269, doi:10.1103/PhysRevLett.20.1265, Bibcode: 1968PhRvL..20.1265S
- Valtonen, M. J. et al. (2008), "A massive binary black-hole system in OJ 287 and a test of general relativity", Nature 452 (7189): 851–853, doi:10.1038/nature06896, PMID 18421348, Bibcode: 2008Natur.452..851V
External links
- Einstein Online – Articles on a variety of aspects of relativistic physics for a general audience; hosted by the Max Planck Institute for Gravitational Physics
- GEO600 home page, the official website of the GEO600 project.
- LIGO Laboratory
- NCSA Spacetime Wrinkles – produced by the numerical relativity group at the NCSA, with an elementary introduction to general relativity
- Courses
- Lectures
- Tutorials
- Einstein's General Theory of Relativity on YouTube (lecture by Leonard Susskind recorded 22 September 2008 at Stanford University).
- Series of lectures on General Relativity given in 2006 at the Institut Henri Poincaré (introductory/advanced).
- General Relativity Tutorials by John Baez.
- Brown, Kevin. "Reflections on relativity". Mathpages.com. http://www.mathpages.com/rr/rrtoc.htm.
- Carroll, Sean M. (1997). "Lecture Notes on General Relativity". arXiv:gr-qc/9712019.
- Moor, Rafi. "Understanding General Relativity". http://www.rafimoor.com/english/GRE.htm.
- Waner, Stefan. "Introduction to Differential Geometry and General Relativity". http://www.zweigmedia.com/diff_geom/tc.html.
- The Feynman Lectures on Physics Vol. II Ch. 42: Curved Space
 |