Physics:Hexatic phase

From HandWiki

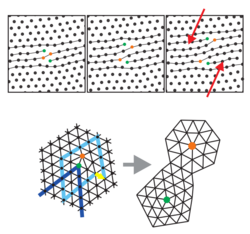
The hexatic phase is a state of matter that is between the solid and the isotropic liquid phases in two dimensional systems of particles. It is characterized by two order parameters: a short-range positional and a quasi-long-range orientational (sixfold) order. More generally, a hexatic is any phase that contains sixfold orientational order, in analogy with the nematic phase (with twofold orientational order). It is a fluid phase, since the shear modulus and the Young's modulus vanish due to the dissociation of dislocations. It is an anisotropic phase, since there exists a director field with sixfold symmetry. The existence of the director field implies that an elastic modulus against drilling or torsion exists within the plane, that is usually called Frank's constant after Frederick C. Frank in analogy to liquid crystals. The ensemble becomes an isotropic liquid (and Frank's constant becomes zero) after the dissociation of disclinations at a higher temperature (or lower density). Therefore, the hexatic phase contains dislocations but no disclinations.

The KTHNY theory of two-step melting by i) destroying positional order and ii) destroying orientational order was developed by John Michael Kosterlitz, David J. Thouless, Bertrand Halperin, David Robert Nelson and A. P. Young in theoretical studies about topological defect unbinding two dimensions. In 2016, M. Kosterlitz and D. Thouless were awarded with the Nobel prize in physics (together with Duncan Haldane) for the idea that melting in 2D is mediated by topological defects. The hexatic phase was predicted by D. Nelson and B. Halperin; it does not have a strict analogue in three dimensions.

Order parameter

The hexatic phase can be described by two order parameters, where the translational order is short ranged (exponential decay) and the orientational order is quasi-long ranged (algebraic decay).

phase translational order orientational order defects
crystalline quasi-long range: [math]\displaystyle{ G_{\vec{G}}(\vec{R}) \propto R^{-\eta_{\vec{G}}} }[/math] long range: [math]\displaystyle{ \lim_{r \to \infty}G_6(\vec{r}) \propto const. }[/math] no defects
hexatic (anisotropic fluid) short range: [math]\displaystyle{ G_{\vec{G}}(\vec{R}) \propto e^{-R/\xi_{\vec{G}}} }[/math] quasi-long range: [math]\displaystyle{ G_6(\vec{r}) \propto r^{-\eta_6} }[/math] dislocations
isotropic fluid short range: [math]\displaystyle{ G_{\vec{G}}(\vec{R}) \propto e^{-R/\xi_{\vec{G}}} }[/math] short range: [math]\displaystyle{ G_6(\vec{r}) \propto e^{-r/\xi_6} }[/math] dislocations and disclinations

Translational order

Dislocations destroy translational order (shearing along the red arrows), but orientational order is still visible, indicated by black lines in one direction (upper part). Disclinations additionally destroy orientational order (lower part).

If the position of atoms or particles is known, then the translational order can be determined with the translational correlation function [math]\displaystyle{ G_{\vec{G}}(\vec{R}) }[/math] as function of the distance between lattice site at place [math]\displaystyle{ \vec{R} }[/math] and the place [math]\displaystyle{ \vec{0} }[/math], based on the two-dimensional density function [math]\displaystyle{ \rho_{\vec{G}}(\vec{R}) = e^{i\vec{G}\cdot [\vec{R}+\vec{u}(\vec{R})]} }[/math] in reciprocal space:

[math]\displaystyle{ G_{\vec{G}}(\vec{R}) = \langle \rho_{\vec{G}}(\vec{R}) \cdot \rho^\ast_{\vec{G}}(\vec{0}) \rangle }[/math]

The vector [math]\displaystyle{ \vec{R} }[/math] points to a lattice site within the crystal, where the atom is allowed to fluctuate with an amplitude [math]\displaystyle{ \vec{u}(\vec{R}) }[/math] by thermal motion. [math]\displaystyle{ \vec{G} }[/math] is a reciprocal vector in Fourier space. The brackets denote a statistical average about all pairs of atoms with distance R an.

The translational correlation function decays fast, i. e. exponential, in the hexatic phase. In a 2D crystal, the translational order is quasi-long range and the correlation function decays rather slow, i. e. algebraic; It is not perfect long range, as in three dimensions, since the displacements [math]\displaystyle{ \vec{u}(\vec{R}) }[/math] diverge logarithmically with systems size at temperatures above T=0 due to the Mermin-Wagner theorem.

A disadvantage of the translational correlation function is, that it is strictly spoken only well defined within the crystal. In the isotropic fluid, at the latest, disclinations are present and the reciprocal lattice vector is not defined any more.

Orientational order

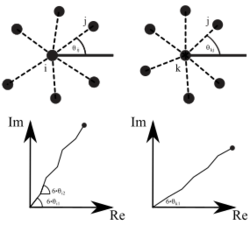
The j nearest neighbours of the i-th particle define the sixfold director field.

The orientational order can be determined by the local director field of a particle at place [math]\displaystyle{ \vec{r}_i }[/math], if the angles [math]\displaystyle{ \theta_{ij} }[/math] are taken, given by the bond to the [math]\displaystyle{ N_i }[/math] nearest neighbours in sixfolded space, normalized with the number of nearest neighbours:

[math]\displaystyle{ \Psi(\vec{r}_i) = \frac{1}{N_i}\sum_{j=1}^{N_i}e^{i6\theta_{ij}} }[/math]

[math]\displaystyle{ \Psi }[/math] is a complex number of magnitude [math]\displaystyle{ |\Psi(\vec{r})| \leq 1 }[/math] and the orientation of the six-folded director is given by the phase. In a hexagonal crystal, this is nothing else but the crystal-axes. The local director field disappears for a particle with five or seven nearest neighbours, as given by dislocations and disclinations [math]\displaystyle{ \Psi \sim 0 }[/math], except a small contribution due to thermal motion. The orientational correlation function between two particles i and k at distance [math]\displaystyle{ \vec{r} = \vec{r}_i - \vec{r}_k }[/math] is now defined using the local director field:

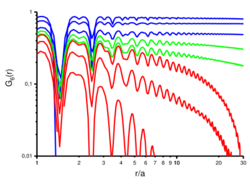
[math]\displaystyle{ G_6(\vec{r}) = \langle \Psi(\vec{r}_i) \cdot \Psi^\ast(\vec{r}_k) \rangle }[/math]

Again, the brackets denote the statistical average about all pairs of particles with distance [math]\displaystyle{ |\vec{r}| = r }[/math]. All three thermodynamic phases can be identified with this orientational correlation function: it does not decay in the 2D crystal but takes a constant value (shown in blue in the figure). The stiffness against local torsion is arbitrarily large, Franks's constant is infinity. In the hexatic phase, the correlation decays with a power law (algebraic). This gives straight lines in a log-log-plot, shown in green in the Figure. In the isotropic phase, the correlations decay exponentially fast, this are the red curved lines in the log-log-plot (in a lin-log-plot, it would be straight lines). The discrete structure of the atoms or particles superimposes the correlation function, given by the minima at half integral distances [math]\displaystyle{ a }[/math]. Particles which are poorly correlated in position, are also poorly correlated in their director.

Orientational correlation of the local director field as function of distance, plotted in blue for the crystal, green for the hexatic phase and red for the isotropic fluid.

See also

External links

References



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Hexatic_phase&oldid=3280928"