Physics:Huygens principle of double refraction

From HandWiki
Short description: Optical principle


Calcite crystal on graph paper.

Huygens principle of double refraction, named after Dutch physicist Christiaan Huygens, explains the phenomenon of double refraction observed in uniaxial anisotropic material such as calcite. When unpolarized light propagates in such materials (along a direction different from the optical axis), it splits into two different rays, known as ordinary and extraordinary rays.[1] The principle states that every point on the wavefront of birefringent material produces two types of wavefronts or wavelets: spherical wavefronts and ellipsoidal wavefronts. These secondary wavelets, originating from different points, interact and interfere with each other. As a result, the new wavefront is formed by the superposition of these wavelets.[1]

Huygens principle of double refraction
Huygens' principle of double refraction.

History

Double refraction in calcite.

The systematic exploration of light polarization began during the 17th century. In 1669, Bartholin made an observation of double refraction in a calcite crystal and documented it in a published work in 1670.[2] Later, in 1690, Huygens identified polarization as a characteristic of light and provided a demonstration using two identical blocks of calcite placed in succession. Each crystal divided an incoming ray of light into two, which Huygens referred to as "regular" and "irregular" (in modern terminology: ordinary and extraordinary). However, if the two crystals were aligned in the same orientation, no further division of the light occurred.[3]

Huygens–Fresnel principle

Huygens–Fresnel principle.

While the Huygens' principle of double refraction explains the phenomenon of double refraction in an optically anisotropic medium, the Huygens–Fresnel principle pertains to the propagation of waves in an optically isotropic medium.[3][4] According to the Huygens–Fresnel principle, each point on a wavefront can be considered a secondary point source of waves, so a new wavefront is formed after the secondary wavelets have traveled for a period equal to one vibration cycle. This new wavefront can be described as an envelope or tangent surface to these secondary wavelets.[5] Understanding and forecasting the classical wave propagation of light is based on the Huygens-Fresnel principle.[3]

Refraction - Huygens-Fresnel principle.

Polarization of light

Electromagnetic wave of the light.

Electric and magnetic fields that are mutually perpendicular and fluctuating give rise to the transverse electromagnetic wave known as light. Electric and magnetic fields are perpendicular to the propagation direction of the wave. For example, if the wave propagation is in the z-direction, both the electric field and the magnetic field lie in the xy-plane. The electric field points in a specific direction in space since it is a vector. The direction of an electromagnetic wave's electric field vector E is referred to as polarization. If the electric field oscillates in the x-direction, the polarization of the light will be linear, along the x-direction.[1][6]

Plane wave equation of the light

The electromagnetic wave equation's sinusoidal solution has the following form:[7][math]\displaystyle{ \begin{align} \mathbf{E} (\mathbf{r}, t) &= \mathbf{E}_0 \cos(\omega t - \mathbf{k} \cdot \mathbf{r} + \phi_0) \\ \mathbf{B} (\mathbf{r}, t) &= \mathbf{B}_0 \cos(\omega t - \mathbf{k} \cdot \mathbf{r} + \phi_0) \end{align} }[/math]where

  • t is time (in seconds),
  • ω is the angular frequency (in radians per second),
  • [math]\displaystyle{ \phi_0 }[/math] is the phase angle constant (in rad), and
  • k = (kx, ky, kz) is the wave vector of the wave (in rad/m).

The wave vector is related to the angular frequency and speed of light c by[math]\displaystyle{ k = | \mathbf{k} | = { \omega \over c } = { 2 \pi \over \lambda } }[/math]

where k is the wavenumber (the magnitude of the wave vector) and λ is the wavelength.

Unpolarized light

If we were able to observe a light wave originating from an ordinary source and directed toward us, such as the light emitted by an incandescent bulb, we would find that it consists of mixture of light waves. These waves exhibit electric field components that fluctuate at a rapid pace, nearly matching the optical frequency itself, with a time scale of approximately 10−14 seconds. Consequently, the direction of oscillation of the electric field vector occurs in all possible planes perpendicular to the direction of the light beam. Unpolarized light is a type of light wave where the electric field vector oscillates in multiple planes. Light emitted by the sun, incandescent lamps, or candle flames is considered to be unpolarized.[1][5]

Types of polarization

The light wave polarization specifies the form and location of the electric field vector's direction at a particular point in space as a function of time (in the plane perpendicular to the propagation direction). There are three possible polarization states for light, depending on where the [math]\displaystyle{ \mathbf{E} }[/math] vector's direction is located. The first is plane or linear polarization, the second is elliptical polarization, and the third is circular polarization.

The light may also be partially polarized in addition to these. The polarization of light cannot be determined by the human eye on its own. However, some animals and insects have a vision that is sensitive to polarization.[1]

Plane linear polarized light

Polarization state of linear polarized light parallel to x axis.

Light waves that exhibit oscillation in a single plane are referred to as plane-polarized light waves. In such waves, the electric field vector (E) oscillates exclusively within a single plane that is perpendicular to the direction of wave propagation. This type of wave is also called a linearly polarized wave since the orientation of the field vector at any given point in space and time lies along a line within a plane perpendicular to the wave's direction of propagation.[1][8]

Isotropic and anisotropic materials

Materials can be classified into two categories based on their isotropy. Materials that are isotropic have the same physical characteristics throughout. In other words, regardless of the direction in which they are measured, their characteristics, such as optical, electrical, and mechanical, stay constant. Gases, liquids, and amorphous solids like glass are instances of isotropic materials.[9] On the other hand, anisotropic materials show various physical characteristics depending on the direction of measurement. Their characteristics are not constant throughout the substance. Crystal structure, molecule orientation, or the presence of preferred axes can all be causes of anisotropy. Crystals, certain polymers, calcite, and numerous minerals are typical examples of anisotropic materials. The physical characteristics of anisotropic materials, such as refractive index, electrical conductivity, and mechanical qualities, can differ depending on the direction of measurement.[9]

Optical axis and types of anisotropic materials

A frequent notion in the study of anisotropic materials, particularly in the context of optics, is the optical axis. It refers to a particular axis within the material along which certain optical characteristics remain unaltered. To put it in another way, the light that travels along the optical axis does not experience anisotropic behaviours on the transverse plane.[10]

Uniaxial birefringence, with the right side representing the negative uniaxial material and the left side representing the positive uniaxial material.

It is possible to further divide anisotropic materials into two categories: uniaxial anisotropic and biaxial anisotropic materials. One optical axis, also referred to as the extraordinary axis, exists in uniaxially anisotropic materials. In these materials, light propagating along the optical axis experience the same effects independently of the polarization. The optical plane, also known as the plane of polarization, is perpendicular to the optical axis. Light exhibits birefringence within this plane, which means that the refractive index and all the phenomena associated to that, depend on the polarization. A common effect that can be observed is the splitting of an incident ray into two rays when propagating in a birefringent medium.[9][10] Due to the presence of two independent optical axes in biaxial anisotropic materials, light travelling in two different directions will experience different optical characteristics.[9]

Positive and negative uniaxial material

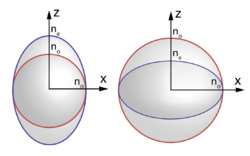
There are two types of uniaxial material depending on the value of index of refraction for the e-ray and o-ray. When the value of the refractive index of the e-ray (ne) is larger than the index of refraction index of the o-ray(n0), the material is positive uniaxial. On the other hand, when the value of refractive index of the e-ray (ne) is less than index of refraction index of the o-ray (n0), the material is negative uniaxial material. Ice and quartz are examples for positive uniaxial material. Calcite and tourmaline are examples of negative uniaxial materials.[1]

Huygens' explanation of double refraction

The ordinary ray (o-ray) has a spherical wavefront because the o-ray has a constant refractive index (n0) independent of propagation direction inside the uniaxial material and the same velocity in all directions. On the other hand, the extraordinary ray (E-ray) has an ellipsoidal wavefront due to its refractive index, which varies with the propagation direction within the uniaxial material, leading to different velocities in different directions. The two wavefronts come into contact at the points where they intersect with the optical axis.[1]

Double refraction in uniaxial material.

When unpolarized light incidents on the birefringent material, the o-ray and e-ray will generate new wavefronts. The new wavefront for the o-ray will be tangent to the spherical wavelets, while the new wavefront for the e-ray will be tangent to the ellipsoidal wavelets. Each plane wavefront propagates straight ahead but with different velocities: V0 for the o-ray and Ve for the e-ray. The direction of the k-vector is always perpendicular to the wavefronts and is calculated from Snell's law. For normal incidence, the o-ray and e-ray having the same k-vector direction. However, the Poynting vector, describing the direction of propagation of optical power, is different for the two rays. The power direction for each ray is determined by connecting the line from the imaginary source on the old wavefront to the intersection point between the new wavefront and the spherical or ellipsoidal wavefront. As a result, the o-ray and e-ray will propagate in different directions with different velocities inside the material. For the e-ray, the angle between the k-vector and the power direction is called walk-off angle.[11]

When a light travels through the crystal, these two wave surfaces follow distinct paths within the crystal. Eventually, two refracted rays emerge as a result of this propagation.[12]

See also

References

  1. ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 al, N. Subrahmanyam et (2012) (in en). A Textbook of Optics. S. Chand Publishing. pp. 492; 498-499; 480-482; 482-483; 484-485; 500-501; 504-507. ISBN 978-81-219-2611-9. https://books.google.com/books?id=6Rrx6HvBtVkC. 
  2. ↑ Shurcliff, William A. (1962-12-31). Polarized Light. doi:10.4159/harvard.9780674424135. ISBN 9780674424111. http://dx.doi.org/10.4159/harvard.9780674424135. 
  3. ↑ 3.0 3.1 3.2 Huygens, Christiaan (1913-04-18). "Treatise on Light.". Science 37 (955): 610–611. doi:10.1126/science.37.955.610. ISSN 0036-8075. http://dx.doi.org/10.1126/science.37.955.610. 
  4. ↑ Wünsch, V. (1988), "Huygens' Principle for Spin Tensor Equations", Huygens' Principle and Hyperbolic Equations (Elsevier): pp. 825–829, doi:10.1016/b978-0-12-307330-3.50022-2, ISBN 9780123073303, http://dx.doi.org/10.1016/b978-0-12-307330-3.50022-2, retrieved 2023-07-04 
  5. ↑ 5.0 5.1 Serway, Raymond A.; Jewett, John W. (2013-01-08) (in en). Physics for Scientists and Engineers. Cengage Learning. pp. 1071–1072, 1175–1177. ISBN 978-1-285-53187-8. https://books.google.com/books?id=bfoWAAAAQBAJ. 
  6. ↑ Born -Wolf, Max - Emil. "Principles of Optics: 60th Anniversary Edition" (in en). pp. 25–30. https://www.ibs.it/principles-of-optics-60th-anniversary-libro-inglese-max-born-emil-wolf/e/9781108477437. 
  7. ↑ "VIII. A dynamical theory of the electromagnetic field". Philosophical Transactions of the Royal Society of London 155: 459–512. 1865-12-31. doi:10.1098/rstl.1865.0008. ISSN 0261-0523. http://dx.doi.org/10.1098/rstl.1865.0008. 
  8. ↑ Shipman, James; Wilson, Jerry D.; Higgins, Charles A. (2012-01-01) (in en). An Introduction to Physical Science. Cengage Learning. pp. 1175–1177. ISBN 978-1-133-10409-4. https://books.google.com/books?id=dxoM93eNPVEC. 
  9. ↑ 9.0 9.1 9.2 9.3 Malgrange, Cécile; Ricolleau, Christian; Schlenker, Michel (2014). "Symmetry and Physical Properties of Crystals". Springer: 187–200. doi:10.1007/978-94-017-8993-6. ISBN 978-94-017-8992-9. http://dx.doi.org/10.1007/978-94-017-8993-6. 
  10. ↑ 10.0 10.1 Chekhova, Maria; Banzer, Peter (2021-03-17). "Polarization of Light". Degruyter: 29–40. doi:10.1515/9783110668025. ISBN 9783110668025. http://dx.doi.org/10.1515/9783110668025. 
  11. ↑ Dmitriev, Valentin G.; Gurzadyan, Gagik G.; Nikogosyan, David N. (1999) (in en). Handbook of Nonlinear Optical Crystals. Springer Series in Optical Sciences. 64. Springer. pp. 9–12. doi:10.1007/978-3-540-46793-9. ISBN 978-3-642-08472-0. https://link.springer.com/book/10.1007/978-3-540-46793-9. 
  12. ↑ Kumar, Arun; Ghatak, Ajoy (2011-01-18). 9780819482167/10.1117/3.861761 Polarization of Light with Applications in Optical Fibers. 1000 20th Street, Bellingham, WA 98227-0010 USA: SPIE. pp. 62–66. doi:10.1117/3.861761. ISBN 978-0-8194-8215-0. https://www.spiedigitallibrary.org/ebooks/TT/Polarization-of-Light-with-Applications-in-Optical-Fibers/eISBN 9780819482167/10.1117/3.861761. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Huygens_principle_of_double_refraction&oldid=3284688"