Physics:Internal resistance

Short description: Impedance of a linear circuit's Thévenin representation

Internal resistance model of a source of voltage, where ε is the electromotive force of the source, R is the load resistance, V is the voltage drop across the load, I is the current delivered by the source, and r is the internal resistance.

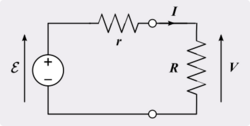
In electrical engineering, a practical electric power source which is a linear circuit may, according to Thévenin's theorem, be represented as an ideal voltage source in series with an impedance. This impedance is termed the internal resistance of the source. When the power source delivers current, the measured voltage output is lower than the no-load voltage; the difference is the voltage drop (the product of current and resistance) caused by the internal resistance. The concept of internal resistance applies to all kinds of electrical sources and is useful for analyzing many types of circuits.

Battery

A battery may be modeled as a voltage source in series with a resistance. These types of models are known as equivalent circuit models. Another common model being physiochemical models that are physical in nature involving concentrations and reaction rates. In practice, the internal resistance of a battery is dependent on its size, state of charge, chemical properties, age, temperature, and the discharge current. It has an electronic component due to the resistivity of the component materials and an ionic component due to electrochemical factors such as electrolyte conductivity, ion mobility, speed of electrochemical reaction and electrode surface area. Measurement of the internal resistance of a battery is a guide to its condition, but may not apply at other than the test conditions. Measurement with an alternating current, typically at a frequency of 1 kHz, may underestimate the resistance, as the frequency may be too high to take into account slower electrochemical processes. Internal resistance depends on temperature; for example, a fresh Energizer E91 AA alkaline primary battery drops from about 0.9 Ω at -40 °C, when the low temperature reduces ion mobility, to about 0.15 Ω at room temperature and about 0.1 Ω at 40 °C. A large part of this drop is due to the increase in the magnitude of the electrolyte diffusion coefficient.

The internal resistance of a battery may be calculated from its open circuit voltage V_NL, load voltage V_FL, and the load resistance R_L:

[math]\displaystyle{ R_{\text{int}} = \left({\frac{ V_{\text{NL}} } { V_{\text{FL}} } - 1 } \right) { R_{\text{L}} } }[/math]

This can also be expressed in terms of the Overpotential η and the current I:

[math]\displaystyle{ R_{int}= \frac{\eta}{I} }[/math]

Many equivalent series resistance (ESR) meters, essentially AC milliohm-meters normally used to measure the ESR of capacitors, can be used to estimate battery internal resistance, particularly to check the state of discharge of a battery rather than obtain an accurate DC value. Some chargers for rechargeable batteries indicate the ESR.

In use, the voltage across the terminals of a disposable battery driving a load decreases until it drops too low to be useful; this is largely due to an increase in internal resistance rather than a drop in the voltage of the equivalent source.

In rechargeable lithium polymer batteries, the internal resistance is largely independent of the state of charge but increases as the battery ages due to the build up of a passivation layer on the electrodes called the solid electrolyte interphase; thus, it is a good indicator of expected life.

See also

• Norton's theorem
• Output impedance

References

• Student Reference Manual for Electronic Instrumentation Laboratories (2nd Edition) - Stanley Wolf & Richard F.M. Smith
• Fundamentals of Electric Circuits (4th Edition) - Charles Alexander & Matthew Sadiku

External links

• Interconnection of two audio units - Output impedance and input impedance

es:Impedancia de salida ja:内部抵抗 tr:İç direnç