Physics:Maxwell–Jüttner distribution

In physics, the Maxwell–Jüttner distribution, sometimes called Jüttner–Synge distribution, is the distribution of speeds of particles in a hypothetical gas of relativistic particles. Similar to the Maxwell–Boltzmann distribution, the Maxwell–Jüttner distribution considers a classical ideal gas where the particles are dilute and do not significantly interact with each other. The distinction from Maxwell–Boltzmann's case is that effects of special relativity are taken into account. In the limit of low temperatures [math]\displaystyle{ T }[/math] much less than [math]\displaystyle{ mc^2/k_\text{B} }[/math] (where [math]\displaystyle{ m }[/math] is the mass of the kind of particle making up the gas, [math]\displaystyle{ c }[/math] is the speed of light and [math]\displaystyle{ k_\text{B} }[/math] is Boltzmann constant), this distribution becomes identical to the Maxwell–Boltzmann distribution. The distribution can be attributed to Ferencz Jüttner, who derived it in 1911. It has become known as the Maxwell–Jüttner distribution by analogy to the name Maxwell–Boltzmann distribution that is commonly used to refer to Maxwell's or Maxwellian distribution.

Definition

Maxwell–Jüttner distribution over Lorentz factor (relativistic Maxwell–Boltzmann), for a gas at different temperatures. Speed is represented in terms of the Lorentz factor.

As the gas becomes hotter and [math]\displaystyle{ k_\text{B}T }[/math] approaches or exceeds [math]\displaystyle{ mc^2 }[/math], the probability distribution for [math]\displaystyle{ \gamma=1/\sqrt{1-v^2/c^2} }[/math] in this relativistic Maxwellian gas is given by the Maxwell–Jüttner distribution:

[math]\displaystyle{ f(\gamma) = \frac{\gamma^2 \,\beta(\gamma)}{\theta \operatorname{K}_2\!\left(\frac{1}{\theta}\right)} e^{-{\gamma}/{\theta}} }[/math]

where [math]\displaystyle{ \beta = \frac {v}{c} = \sqrt{1-1/\gamma^2}, }[/math] [math]\displaystyle{ \theta=\frac{k_\text{B}T}{mc^2}, }[/math] and [math]\displaystyle{ \operatorname{K}_2 }[/math] is the modified Bessel function of the second kind.

Alternatively, this can be written in terms of the momentum as [math]\displaystyle{ f(\mathbf{p}) = \frac{1}{4\pi m^3c^3\theta\operatorname{K}_2\!\left(\frac{1}{\theta}\right)} e^{-\frac{\gamma(p)}{\theta}} }[/math] where [math]\displaystyle{ \gamma(p) = \sqrt{1+\left(\frac{p}{mc}\right)^2} }[/math]. The Maxwell–Jüttner equation is covariant, but not manifestly so, and the temperature of the gas does not vary with the gross speed of the gas.

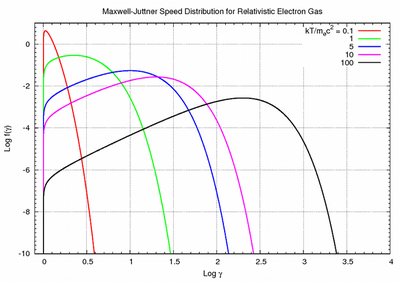
Jüttner distribution graph

A visual representation of the distribution in particle velocities for plasmas at four different temperatures:

Where thermal parameter has been defined as [math]\displaystyle{ \mu = \frac{mc^2}{k_\text{B}T} = \frac{1}{\theta} }[/math].

The four general limits are:

• ultrarelativistic temperatures [math]\displaystyle{ \mu \ll 1 \iff \theta \gg 1 }[/math]
• relativistic temperatures: [math]\displaystyle{ \mu \lt 1 \iff \theta \gt 1 }[/math],
• weakly (or mildly) relativistic temperatures: [math]\displaystyle{ \mu \gt 1 \iff \theta \lt 1 }[/math],
• low temperatures: [math]\displaystyle{ \mu \gg 1 \iff \theta \ll 1 }[/math],

Limitations

Some limitations of the Maxwell–Jüttner distributions are shared with the classical ideal gas: neglect of interactions, and neglect of quantum effects. An additional limitation (not important in the classical ideal gas) is that the Maxwell–Jüttner distribution neglects antiparticles.

If particle-antiparticle creation is allowed, then once the thermal energy [math]\displaystyle{ k_\text{B}T }[/math] is a significant fraction of [math]\displaystyle{ mc^2 }[/math], particle-antiparticle creation will occur and begin to increase the number of particles while generating antiparticles (the number of particles is not conserved, but instead the conserved quantity is the difference between particle number and antiparticle number). The resulting thermal distribution will depend on the chemical potential relating to the conserved particle–antiparticle number difference. A further consequence of this is that it becomes necessary to incorporate statistical mechanics for indistinguishable particles, because the occupation probabilities for low kinetic energy states becomes of order unity. For fermions it is necessary to use Fermi–Dirac statistics and the result is analogous to the thermal generation of electron–hole pairs in semiconductors. For bosonic particles, it is necessary to use the Bose–Einstein statistics.

Perhaps most significantly, the basic [math]\displaystyle{ \text{MB} }[/math] distribution has two main issues: it does not extend to particles moving at relativistic speeds, and  it assumes anisotropic temperature (where each DoF does not have the same translational kinetic energy). While the classic Maxwell–Jüttner distribution generalizes for the case of special relativity, it fails to consider the anisotropic description.

Derivation

The Maxwell–Boltzmann ([math]\displaystyle{ \text{MB} }[/math]) distribution [math]\displaystyle{ \operatorname{pdf}_\text{MB} }[/math] describes the velocities [math]\displaystyle{ \mathbf{u} }[/math] or the kinetic energy [math]\displaystyle{ \varepsilon = \frac{1}{2} m\mathbf{u}^2 }[/math] of the particles at thermal equilibrium, far from the limit of the speed of light, i.e:

[math]\displaystyle{ \operatorname{pdf}_\text{MB}( \mathbf{p};\theta) = \left(\pi m^2 \theta^2\right)^{-d/2} e^{-\frac{\mathbf{p}^2/2m}{k_\text{B}T}} }[/math]

(1a)

[math]\displaystyle{ \theta \equiv \sqrt{2{k_\text{B}T}/{m}},\ \ u \ll c }[/math]

Or, in terms of the kinetic energy:

[math]\displaystyle{ \operatorname{pdf}_\text{MB}(\varepsilon;T) = \frac{(k_\text{B}T)^{-d/2}}{\Gamma\left(\frac{d}{2}\right)} e^{-{\varepsilon}/{k_\text{B}T}} \varepsilon^{\frac{1}{2}d-1} }[/math]

(1b)

[math]\displaystyle{ \varepsilon \ll mc^2 }[/math]

where [math]\displaystyle{ \theta }[/math] is the temperature in speed dimensions, called thermal speed, and d denotes the kinetic degrees of freedom of each particle. (Note that the temperature is defined in the fluid’s rest frame, where the bulk speed [math]\displaystyle{ \mathbf{u}_b }[/math] is zero. In the non-relativistic case, this can be shown by using [math]\displaystyle{ \varepsilon = \frac{1}{2} m (\mathbf{u}-\mathbf{u}_b)^2 }[/math].

The relativistic generalization of Eq. (1a), that is, the Maxwell–Jüttner ([math]\displaystyle{ \text{MJ} }[/math]) distribution, is given by:

[math]\displaystyle{ \operatorname{pdf}_\text{MJ}(\gamma)\propto\gamma^2\beta(\gamma ) \, e^{-\frac{\gamma}{\theta}},\theta \equiv \frac{k_\text{B}T}{E_0},\ E_0 = mc^2 }[/math]

(2)

where [math]\displaystyle{ \beta \equiv {\mathbf{u}}/{c} }[/math] and [math]\displaystyle{ \gamma(\beta) = (1-\beta^2)^{-{1}/{2}} }[/math]. (Note that the inverse of the unitless temperature [math]\displaystyle{ \theta }[/math] is the relativistic coldness [math]\displaystyle{ \zeta }[/math], Rezzola and Zanotti, 2013.) This distribution (Eq. 2) can be derived as follows. According to the relativistic formalism for the particle momentum and energy, one has

[math]\displaystyle{ \mathbf{p =}mc \, \gamma\left( \beta \right) \, \mathbf{\beta},\ E\left( \beta \right) = \gamma(\beta) \, E_0 }[/math]

(3)

While the kinetic energy is given by [math]\displaystyle{ \varepsilon = E - E_0 = (\gamma - 1) \, E_0 }[/math]. The Boltzmann distribution of a Hamiltonian is [math]\displaystyle{ \operatorname{pdf}_\text{MJ}(H) \propto e^{- \frac{H}{k_\text{B}T} }. }[/math] In the absence of a potential energy, [math]\displaystyle{ H }[/math] is simply given by the particle energy [math]\displaystyle{ E }[/math], thus:

[math]\displaystyle{ \operatorname{pdf}_\text{MJ}\left( E \right)\propto e^{- \frac{E}{k_\text{B}T}} \propto e^{- \frac{\gamma}{\theta}} }[/math]

(4a)

(Note that [math]\displaystyle{ E }[/math] is the sum of the kinetic [math]\displaystyle{ \varepsilon }[/math] and inertial energy [math]\displaystyle{ E_0,\frac{\varepsilon}{k_\text{B}T} = \frac{\gamma - \ 1}{\theta} }[/math]). Then, when one includes the [math]\displaystyle{ d }[/math]-dimensional density of states:

[math]\displaystyle{ \operatorname{pdf}_\text{MJ}(\gamma) \propto p( \gamma)^{d - 1}\frac{ \mathrm{d}p(\gamma)} \mathrm{d}\gamma \, e^{-\frac{\gamma}{\theta}} }[/math]

(4b)

So that:

[math]\displaystyle{ \begin{align} \int \operatorname{pdf}_\text{MJ}(\mathbf{p}) \mathrm{d}p_1\cdots \mathrm{d}p_d &\propto\int e^{-\frac{E(\mathbf{p})}{k_\text{B}T}} \mathrm{d}p_1\cdots \mathrm{d}p_d \\[1ex] &= \int e^{-\frac{E( \gamma\Omega_d)}{k_\text{B}T} } \mathrm{d}\Omega_d p^{d-1} \mathrm{d}p \\[1ex] &= \int\limits_{\Omega_d} e^{- \frac{E(\gamma\Omega_d)}{k_\text{B}T} } \, \left(p(\gamma)^{d-1}\frac{ \mathrm{d}p(\gamma)}{\mathrm{d}\gamma} \right)\mathrm{d}\Omega_d\mathrm{d}\gamma \end{align} }[/math]

Where [math]\displaystyle{ \mathrm{d}\Omega_d }[/math] denotes the [math]\displaystyle{ d }[/math]-dimensional solid angle. For isotropic distributions, one has

[math]\displaystyle{ \int \operatorname{pdf}_\text{MJ}(p) \mathrm{d}p_1\cdots \mathrm{d}p_d\propto \int e^{-\frac{E(p)}{k_\text{B}T}} \left(p(\gamma)^{d-1}\frac{ \mathrm{d}p(\gamma)}{ \mathrm{d}\gamma}\right) \mathrm{d}\Omega_d \mathrm{d}\gamma\equiv \int\limits_{\Omega_d} \mathrm{d}\Omega_d\, \int P_{MJ}(\gamma) \mathrm{d}\gamma }[/math]

(5a)

or

[math]\displaystyle{ \operatorname{pdf}_\text{MJ}(\gamma)\propto e^{-\frac{E(\gamma)}{k_\text{B}T}}\, p(\gamma)^{d-1}\frac{ \mathrm{d}p(\gamma)}{ \mathrm{d}\gamma} }[/math]

(5b)

Then, [math]\displaystyle{ \mathrm{d}(\gamma\beta) = \gamma (\gamma^2-1)^{- \frac{1}{2}} \mathrm{d}\gamma = \beta^{-1}\mathrm{d}\gamma }[/math] so that:

[math]\displaystyle{ \begin{align} p\left(\gamma\right)^{d-1}\frac{ \mathrm{d}p\left(\gamma\right)}{ \mathrm{d}\gamma} &= (mc)^d (\gamma\beta)^{d-1} \frac{\mathrm{d}( \gamma\beta)}{\mathrm{d}\gamma} \\ &= ( mc )^d \gamma^{d - 1}\beta^{d - 2}, \end{align} }[/math]

(6)

Or:

[math]\displaystyle{ \operatorname{pdf}_\text{MJ}(\gamma)\propto \gamma^{d-1}\beta^{d-2} e^{-\frac{\gamma}{\theta}} \propto\gamma(\gamma^2-1)^{\frac{d}{2}-1}\, e^{-\frac{\gamma}{\theta}} }[/math]

(7)

Now, because [math]\displaystyle{ \frac{E}{k_\text{B}T} = \frac{\gamma}{\theta} }[/math]. Then, one normalises the distribution Eq. (7). One sets

[math]\displaystyle{ \operatorname{pdf}_\text{MJ}(p,\theta) \mathrm{d}p_1\cdots \mathrm{d}p_d =N\, e^{-{\gamma(p)}/{\theta}} \mathrm{d}p_1\cdots \mathrm{d}p_d }[/math]

(8)

And the angular integration: [math]\displaystyle{ \mathrm{d}p_1 \cdots \mathrm{d}p_d = B_d p^{d - 1} \mathrm{d}p = \frac{1}{2} B_d\left( mc \right)^d\left(\left( \frac{p}{mc} \right)^2 \right)^{\frac{d}{2}-1} \mathrm{d}\left( \frac{p}{mc} \right)^2, }[/math]

Where [math]\displaystyle{ B_d = \frac{2\pi^{d}/{2}}{\Gamma\left( \frac{d}{2} \right)} }[/math] is the surface of the unit d-dimensional sphere. Then, using the identity [math]\displaystyle{ \gamma^2 = \left( \frac{p}{mc} \right)^2 + 1 }[/math] one has:

[math]\displaystyle{ \operatorname{pdf}_\text{MJ}(\mathbf{p};\theta) \mathrm{d}p_1 \cdots \mathrm{d}p_d = N \, \frac{1}{2} B_d\left( mc \right)^{d} \, e^{-\frac{\gamma}{\theta}} (\gamma^2-1)^{\frac{d}{2}-1} \mathrm{d}(\gamma^2-1). }[/math]

(9)

and

[math]\displaystyle{ \begin{align} 1 &= \int_{-\infty}^\infty \operatorname{pdf}_\text{MJ}(\mathbf{p};\theta ) \mathrm{d}p_1\cdots \mathrm{d}p_d \\[1ex] &= N \, \frac{1}{2}B_d(mc)^d \, \int_1^\infty e^{- \frac{\gamma}{\theta} } (\gamma^2-1)^{\frac{d}{2}-1} \mathrm{d}(\gamma^2-1) \\[1ex] &= N \, \frac{1}{2} B_d \left( \frac{d}{2}\right)^{-1} (mc)^d \theta^{- 1} \, \int_1^\infty e^\frac{\gamma}{\theta} (\gamma^2-1)^\frac{d}{2} \mathrm{d}\gamma \\[1ex] &= N \, \frac{1}{2}B_d\left( \frac{d}{2} \right)^{- 1}(mc)^d\theta^{- 1} \, I_d, \end{align} }[/math]

(10)

Where one has defined the integral:

[math]\displaystyle{ I_d \equiv \int_1^\infty e^{- {\gamma}/{\theta}} (\gamma^2-1)^{{d}/{2}} \mathrm{d}\gamma. }[/math]

(11)

The Macdonald function (Modified Bessel function of the II kind) (Abramowitz and Stegun, 1972, p.376) is defined by:

[math]\displaystyle{ \operatorname{K}_n(z)\equiv \frac{\pi^\frac{1}{2}(\frac{1}{2}z)^n}{\Gamma(n+\frac{1}{2})} \int_1^\infin e^{-z\gamma}(\gamma^2-1)^{n-\frac{1}{2}} \mathrm{d}\gamma }[/math]

(12)

So that, by setting [math]\displaystyle{ n = \frac{d + 1}{2},\ z = \frac{1}{\theta} }[/math] one obtains:

[math]\displaystyle{ I_d = \Gamma\left(\frac{d}{2}+1\right) \pi^{-\frac{1}{2}} \operatorname{K}_\frac{d+1}{2} \left(\frac{1}{\theta}\right) (2\theta)^\frac{d+1}{2} }[/math]

(13)

Hence,

[math]\displaystyle{ N^{-1} = \frac{\pi^\frac{d}{2}}{\Gamma\left(\frac{d}{2}\right)} \left( \frac{d}{2}\right)^{-1} \Gamma\left( \frac{d}{2}+1\right )\pi^{-\frac{1}{2}}\operatorname{K}_\frac{d+1}{2}\left( \frac{1}{\theta}\right) (mc)^d (2\theta )^\frac{d+1}{2} = \pi^\frac{d-1}{2} 2^{-\frac{d+1}{2}}(mc)^d \, \theta^\frac{d-1}{2} \operatorname{K}_\frac{d+1}{2} \left(\frac{1}{\theta} \right), }[/math]

(14a)

Or

[math]\displaystyle{ N = \ \pi^\frac{1-d}{2}2^{-\frac{d + 1}{2}}(mc)^{-d} \, \theta^\frac{1-d}{2}\operatorname{K}_\frac{d+1}{2}\left( \frac{1}{\theta} \right)^{- 1} , }[/math]

(14b)

The inverse of the normalization constant gives the partition function [math]\displaystyle{ Z \equiv \frac{1}{N}: }[/math]

[math]\displaystyle{ Z = \pi^\frac{d-1}{2} 2^{- \frac{d+1}{2}}(mc)^d \, \theta^\frac{d-1}{2} \operatorname{K}_\frac{d+1}{2} \left( \frac{1}{\theta} \right), }[/math]

(14c)

Therefore, the normalized distribution is:

[math]\displaystyle{ \operatorname{pdf}_\text{MJ}(p;\theta) \mathrm{d}p_1\cdots \mathrm{d}p_d = \pi^\frac{1-d}{2}2^{-\frac{d+1}{2}}(mc)^{-d}\, \theta^\frac{1-d}{2}\operatorname{K}_\frac{d+1}{2}\left(\frac{1}{\theta}\right)^{-1} e^{-\frac{\gamma(p)}{\theta}} \mathrm{d}p_1\cdots \mathrm{d}p_d }[/math]

(15a)

Or one may derive the normalised distribution in terms of:

[math]\displaystyle{ \operatorname{pdf}_\text{MJ}(\gamma;\theta) \mathrm{d}\gamma = \frac{\pi^\frac{1}{2}2^\frac{1-d}{2}}{{\Gamma{\left(\frac{d}{2}\right)}}}\operatorname{K}_\frac{d+1}{2}\left(\frac{1}{\theta}\right)^{-1}\theta^\frac{1-d}{2}e^{-\frac{\gamma}{\theta}}(\gamma^2-1)^{\frac{d}{2}-1} \gamma \mathrm{d}\gamma }[/math]

(15b)

Note that [math]\displaystyle{ \theta }[/math] can be shown to coincide with the thermodynamic definition of temperature.

Also useful is the expression of the distribution in the velocity space. Given that [math]\displaystyle{ \frac{\mathrm{d}(\beta\gamma)}{\mathrm{d}\beta} = \gamma^3 }[/math], one has:

[math]\displaystyle{ \begin{align} \mathrm{d}p_1 \cdots \mathrm{d}p_d = p^{d-1} \mathrm{d}p \mathrm{d}\Omega_d &= (mc)^d \gamma^{d - 1}\beta^{d - 1}\frac{\mathrm{d}(\beta\gamma)}{\mathrm{d}\beta}\mathrm{d}\beta\mathrm{d}\Omega_d \\ &= (mc)^d \gamma^{d + 2}\beta^{d - 1}\text{dβd}\Omega_d\\[1ex] &= (mc)^d \gamma^{d+2} \mathrm{d}\beta_1\cdots \mathrm{d}\beta_d \end{align} }[/math]

Hence

[math]\displaystyle{ \operatorname{pdf}_\text{MJ}( \mathbf{\beta};\theta ) \mathrm{d}\beta_1 \cdots \mathrm{d}\beta_d = \pi^\frac{1-d}{2}2^{-\frac{d+1}{2}} \, \theta^\frac{1-d}{2}\operatorname{K}_\frac{d+1}{2}\left( \frac{1}{\theta}\right)^{-1} e^{-\frac{\gamma(\beta)}{\theta}} \gamma( \beta)^{d+2} \mathrm{d}\beta_1\cdots \mathrm{d}\beta_d }[/math]

(15c)

Take [math]\displaystyle{ d = 3 }[/math] (the “classic case” in our world):

[math]\displaystyle{ \operatorname{pdf}_\text{MJ}(p;\theta) \mathrm{d}p_1 \cdots \mathrm{d}p_d = \frac{1}{4\pi}(mc)^{-3} \, \frac{1}{\theta}\operatorname{K}_2\left( \frac{1}{\theta} \right)^{-1} \, e^{- \frac{\gamma(\mathbf{p)}\ }{\theta}} \mathrm{d}p_1 \mathrm{d}p_2 \mathrm{d}p_3 }[/math]

(16a)

And

[math]\displaystyle{ \operatorname{pdf}_\text{MJ}(\gamma;\theta) \mathrm{d}\gamma = \frac{1}{\theta}\operatorname{K}_2\left( \frac{1}{\theta} \right)^{- 1} \, e^{- \frac{\gamma}{\theta}}(\gamma^2-1 )^\frac{1}{2} \gamma\mathrm{d}\gamma }[/math]

(16b)

[math]\displaystyle{ \operatorname{pdf}_\text{MJ}(\beta;\theta) \mathrm{d}\beta_1 \mathrm{d}\beta_2 \mathrm{d}\beta_3 = \frac{4}{\pi} \, \frac{1}{\theta}\operatorname{K}_2\left( \frac{1}{\theta} \right)^{-1} \, e^{- \frac{\gamma(\beta)}{\theta}} \gamma( \beta)^5 \mathrm{d}\beta_1 \mathrm{d}\beta_2 \mathrm{d}\beta_3 }[/math]

(16c)

Note that when the [math]\displaystyle{ \text{MB} }[/math] distribution clearly deviates from the [math]\displaystyle{ \text{MJ} }[/math] distribution of the same temperature and dimensionality, one can misinterpret and deduce a different [math]\displaystyle{ \text{MB} }[/math]distribution that will give a good approximation to the [math]\displaystyle{ \text{MJ} }[/math] distribution. This new [math]\displaystyle{ \text{MB} }[/math]distribution can be either:

• a convected [math]\displaystyle{ \text{MB} }[/math] distribution, that is, an [math]\displaystyle{ \text{MB} }[/math] distribution with the same dimensionality, but with different temperature [math]\displaystyle{ T_\text{MB} }[/math] and bulk speed [math]\displaystyle{ \mathbf{u}_b }[/math] (or bulk energy [math]\displaystyle{ E_b\equiv \frac{1}{2} m\left(\mathbf{u} + \mathbf{u}_b\right)^2 }[/math])
• an [math]\displaystyle{ \text{MB} }[/math] distribution with the same bulk speed, but with different temperature [math]\displaystyle{ T_\text{MB} }[/math] and degrees of freedom [math]\displaystyle{ d_\text{MB} }[/math]. These two types of approximations are illustrated.

Other properties

The [math]\displaystyle{ \text{MJ} }[/math] probability density function is given by:

[math]\displaystyle{ \operatorname{pdf}_\text{MJ}(\gamma) = \frac{1}{\theta \operatorname{K}_2\!\left(\frac{1}{\theta}\right)} \gamma^2 \,\beta(\gamma) e^{-{\gamma}/{\theta}} }[/math]

This means that a relativistic non-quantum particle with parameter [math]\displaystyle{ \theta }[/math] has a probability of [math]\displaystyle{ \operatorname{pdf}_\text{MJ}(\gamma)\mathrm{d}\gamma }[/math] of having its Lorentz factor in the interval [math]\displaystyle{ [\gamma,\gamma+\mathrm{d}\gamma] }[/math].

The [math]\displaystyle{ \text{MJ} }[/math] cumulative distribution function is given by:

[math]\displaystyle{ \operatorname{cdf}_\text{MJ}(\gamma) = \frac{1}{\theta \operatorname{K}_2\left(\dfrac{1}{\theta}\right)} \int_1^\gamma {\gamma^\prime}^2 \sqrt{1-\frac{1}{{\gamma^\prime}^2}} \, e^{-\gamma' / \theta} \mathrm{d}\gamma' }[/math]

That has a series expansion at [math]\displaystyle{ \gamma = 1 }[/math]:

[math]\displaystyle{ \operatorname{cdf}_\text{MJ}(\gamma) = \frac{2\sqrt{2}}{3} \frac{e^{-{1}/{\theta}}}{\theta \operatorname{K}_2\left(\frac{1}{\theta}\right)} {\sqrt{\gamma-1}}^3 + \frac{1}{5\sqrt{2}} \frac{(5\theta-4) e^{-{1}/{\theta}}}{\theta^2\operatorname{K}_2\left(\frac{1}{\theta}\right)} {\sqrt{\gamma-1}}^5 + \mathcal{O}\left({\sqrt{\gamma-1}}^7 \right) }[/math]

By definition [math]\displaystyle{ \lim_{\gamma\to\infty} \operatorname{cdf}_\text{MJ}(\gamma) = 1 }[/math], regardless of the parameter [math]\displaystyle{ \theta }[/math] .

To find the average speed, [math]\displaystyle{ \langle v\rangle_\text{MJ} }[/math] , one must compute [math]\displaystyle{ \int_1^\infty \operatorname{pdf}_\text{MJ}(\gamma) \, v(\gamma) \,\mathrm{d}\gamma }[/math] , where [math]\displaystyle{ v(\gamma) = c\sqrt{1-{1}/{\gamma^2}} }[/math] is the speed in terms of its Lorentz factor. The integral simplifies to the closed- form expression:

[math]\displaystyle{ \langle v\rangle_\text{MJ} = 2c \frac{\theta(\theta+1) e^{-{1}/{\theta}}}{\operatorname{K}_2\left(\frac{1}{\theta}\right)} }[/math]

This closed formula for [math]\displaystyle{ \langle v\rangle_\text{MJ} }[/math] has a series expansion at [math]\displaystyle{ \theta = 0 }[/math]:

[math]\displaystyle{ \frac{1}{c}\langle v\rangle_\text{MJ} = \sqrt{\frac{8}{\pi}}\sqrt{\theta} -\frac{7}{2\sqrt{2\pi}}{\sqrt{\theta}}^3 + \mathcal{O}\left({\sqrt{\theta}}^5\right) }[/math]

Or substituting the definition for the parameter [math]\displaystyle{ \theta }[/math] : [math]\displaystyle{ \langle v\rangle_\text{MJ} = \sqrt{\frac{8}{\pi}\frac{k_\text{B}T}{m}\;} -\frac{7}{2\sqrt{2\pi}} \frac{1}{c^2}{\sqrt{\frac{k_\text{B}T}{m}\;}}^3 + \cdots }[/math]

Where the first term of the expansion, which is independently of [math]\displaystyle{ c }[/math] , corresponds to the average speed in the Maxwell–Boltzmann distribution, [math]\displaystyle{ \langle v\rangle_\text{MB} = \sqrt{\frac{8}{\pi}\frac{k_\text{B}T}{m}\;} }[/math], whilst the following are relativistic corrections.

This closed formula for [math]\displaystyle{ \langle v\rangle_\text{MJ} }[/math] has a series expansion at [math]\displaystyle{ \theta = \infty }[/math]:

[math]\displaystyle{ \frac{1}{c}\langle v\rangle_\text{MJ} = 1 - \frac{1}{4}\frac{1}{\theta^2} + \mathcal{O}\left(\frac{1}{\theta^3}\right) }[/math]

Or substituting the definition for the parameter [math]\displaystyle{ \theta }[/math]:

[math]\displaystyle{ \langle v\rangle_\text{MJ} = c -\frac{1}{4} c^5 \frac{m^2}{{k_\text{B}}^2T^2} + \cdots }[/math]

Where it follows that [math]\displaystyle{ c }[/math] is an upper limit to the particle's speed, something only present in a relativistic context, and not in the Maxwell–Boltzmann distribution.