Physics:Moving heat source model for thin plates

File:Thinplate.webm Moving heat sources is a topic in transient heat transfer that is applicable to engineering problems, particularly welding engineering. In the early 20th Century, welding engineers began studying moving heat sources, both empirically and theoretically. Depending on welding parameters, plate geometry and material properties, the solution takes three different forms: semi-infinite, intermediate, or thin plate. The temperature distribution and cooling rates can be determined from theoretical solutions to the problem, allowing engineers to better understand the consequences of heat sources on weldability and end item performance.

Empirical Solutions

In the 1930s, Portevin and Seferian attempted to experimentally determine heat transfer characteristics in welding. They correlated the effects of several factors—material properties, welding process, and part dimensions—on temperature distribution, by performing oxyacetylene (gas) and covered electrode (arc) welds on plates and bars of various profiles, and multiple materials, including steel, copper, and aluminum. Their work showed that arc welding temperature gradients were steeper and cooling rates were faster than those of gas welding, which were more sensitive to material thickness than those of arc welding. In addition to process, material properties, and dimensions, the authors noted that preheat played a role in temperature distribution.

Claussen and Sparagen did not detail other attempts to determine temperature distribution in welding, because the variety of approaches employed by the investigators resulted in data that were not comparable. They did note that the data generally revealed the effect of weld process on heat affected zone (HAZ) width, with gas welding having the widest HAZ, bare electrode arc processes the narrowest, and covered electrode falling in the middle.

Theoretical Solutions

Until the mid-1930s, the study of the theory of heat transfer from a moving source was neglected, and temperature distribution due to moving heat sources could only be calculated approximately. In 1935, Daniel Rosenthal published the first literature applying the exact theory of heat flow from a moving source to arc welding. Rosenthal's theoretical model included several assumptions:

• Material properties are constant,
• The heat source is a point source,
• The surface of the work piece does not lose heat to the atmosphere,
• Heat created by the Joule effect is neglected

Rosenthal's solution has been shown to agree well with measured results over a wide range of parameters, although with some scattering of data. The assumption of a point, line, or plane heat source leads to inaccuracy in the vicinity of the fusion zone (where temperature is within about 20% of the melting temperature) and prohibits predicting the shape of the weld pool. Following Rosenthal, researchers were able to approximate weld pool shape by assuming a Gaussian heat source defined by the equation:

[math]\displaystyle{ Q(x,y)= {q\over 2\pi\sigma^2}e^{-{(x^2+y^2)\over2\sigma^2}} }[/math]

where:

• Q = heat source,
• q = net power input,
• σ = distribution parameter.

and later, other heat source distributions, such as semi-ellipsoidal and double ellipsoidal.

Governing Heat Transfer Problem

The governing equation for three-dimensional transient heat transfer in a solid of semi-infinite dimensions, no heat generation, and no surface losses is:

[math]\displaystyle{ \lambda{\partial^2\theta\over\partial x^2}+\lambda{\partial^2\theta\over\partial y^2}+\lambda{\partial^2\theta\over\partial z^2} = {\rho C}{\partial\theta\over\partial t} }[/math]

where:

• θ = temperature,
• x = direction parallel to weld travel,
• y = direction in plane and perpendicular to weld travel,
• z = through-thickness direction,
• λ = thermal conductivity,
• ρ = density,
• t = time,
• C = specific heat.

In the case of a moving heat source applied to a plate that is so thin that temperature does not vary in the through-thickness dimension, the third term becomes zero, and the problem is two-dimensional conduction. The factors that determine whether temperature varies through the thickness include:

• welding speed (increases thermal gradient in through thickness direction),
• thermal diffusivity (decreases thermal gradient in through thickness direction),
• thickness (increases thermal gradient in through thickness direction).

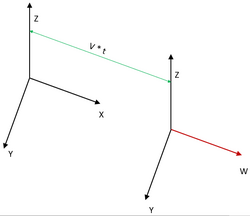
The problem is further simplified by taking advantage of the quasi-stationary state in welding, where temperature distribution from the perspective of a coordinate system that moves with the heat source is constant in time. The through thickness direction and direction perpendicular to the direction of travel are unchanged in the moving coordinate system, but the direction parallel to travel is related to the longitudinal direction of the fixed coordinate system by the equation:

[math]\displaystyle{ w=x-Vt }[/math]

Moving coordinate system at time, t, traveling at speed, V, parallel to the x-direction of a fixed coordinate system.

where:

• w = moving coordinate system longitudinal direction,
• V = weld feed speed,
• x = fixed coordinate system longitudinal direction.

A heat flux boundary condition attributed to Rosenthal is to consider the rate of energy (power) transferred from the arc to the plate as equal to the heat transferred outward from a cylinder with height equal to the plate thickness and an infinitely small radius at the origin:

[math]\displaystyle{ P=\lim_{r \to 0}-{\partial\theta \over \partial r}2\pi r\lambda h }[/math]

where:

• P = power,
• r = distance from point source,
• h = plate thickness.

Another boundary condition is that temperature remains constant at distances far from the point source. Because the boundary conditions and two-dimensional differential equation can be satisfied by a solution that is dependent on distance from the source, a cylindrical coordinate system is used, with:

[math]\displaystyle{ r=(w^2+y^2)^{1\over2} }[/math]

The resulting cylindrical differential equation is:

[math]\displaystyle{ {\partial^2\varphi\over\partial r^2}+{1\over r}{\partial\varphi\over\partial r} - {\Bigl({V\over 2\kappa}\Bigr)}^2\varphi=0 }[/math]

where φ is a function that will be determined later.

Solution

Plots of modified Bessel functions of the second kind for orders 0, 1, and 2.

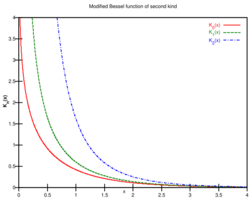
The solution of the radial "quasi-stationary" equation is the modified Bessel function of the second kind and zeroth order:

[math]\displaystyle{ \varphi=K_0\Bigl({Vr\over 2\kappa}\Bigl) }[/math]

Substituting φ into the equation Rosenthal assumed for the solution of the original differential equation:

[math]\displaystyle{ \theta=\theta_0+\Biggl(\frac{P}{2\pi\lambda h}\Biggr)e^{\Bigl(-\frac{Vw}{2\kappa}\Bigr)}K_0\Biggl(\frac{Vr}{2\kappa}\Biggr) }[/math]

Finite Element Analysis

Finite element analysis (FEA) eliminates the assumption of non-constant material properties, and allows the use of non-axisymmetric, three-dimensional heat sources such as ellipsoidal and double ellipsoidal distributions.

The double ellipsoidal heat source distribution presented by Goldak is intended to be flexible, to be used to analyze deep or shallow welds, and asymmetric geometry. The Goldak model has been shown to agree well with experimental results on thick section submerged arc weld (SAW) on steel plate, partial penetration electron beam weld (EBW) on steel plate, and gas tungsten arc weld (GTAW) on thin austenitic stainless steel plate.

Applications

Solution of temperature distribution and cooling rate due to a moving heat source has several practical uses in welding engineering, including:

• microstructure,
• joint strength,
• residual stress,
• cold cracking,
• size of HAZ,
• distortion.

which are dependent on cooling time through temperature ranges (800C - 500C and 400C - 150C) for steels, as well as time spent at elevated temperatures. Rosenthal's solution can be manipulated to determine critical cooling rates, and select optimal preheat and interpass temperatures. Goldak's method has been shown to more accurately calculate 800C - 500C cooling rate than Rosenthal's for Goldak's SAW and EBW experiments. Goldak's method has been shown to be comparable to Gaussian and semi-ellipsoidal FEM models of Hashemzadeh's GTAW expirment.

See also

• Moving Heat Source Model for Semi-infinite Plate