Physics:Multipole magnet
Multipole magnets are magnets built from multiple individual magnets, typically used to control beams of charged particles. Each type of magnet serves a particular purpose.
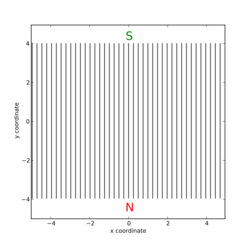
- Dipole magnets are used to bend the trajectory of particles
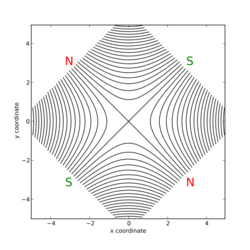
- Quadrupole magnets are used to focus particle beams
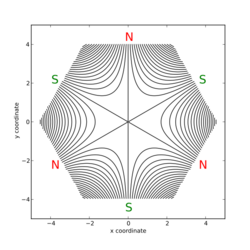
- Sextupole magnets are used to correct for chromaticity introduced by quadrupole magnets[1]
Magnetic field equations
The magnetic field of an ideal multipole magnet in an accelerator is typically modeled as having no (or a constant) component parallel to the nominal beam direction ([math]\displaystyle{ z }[/math] direction) and the transverse components can be written as complex numbers:[2]
[math]\displaystyle{ B_x + i B_y = C_n \cdot ( x - iy )^{n-1} }[/math]
where [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] are the coordinates in the plane transverse to the nominal beam direction. [math]\displaystyle{ C_n }[/math] is a complex number specifying the orientation and strength of the magnetic field. [math]\displaystyle{ B_x }[/math] and [math]\displaystyle{ B_y }[/math] are the components of the magnetic field in the corresponding directions. Fields with a real [math]\displaystyle{ C_n }[/math] are called 'normal' while fields with [math]\displaystyle{ C_n }[/math] purely imaginary are called 'skewed'.
| n | name | magnetic field lines | example device |
|---|---|---|---|
| 1 | dipole | ||
| 2 | quadrupole | ||
| 3 | sextupole |
Stored energy equation
For an electromagnet with a cylindrical bore, producing a pure multipole field of order [math]\displaystyle{ n }[/math], the stored magnetic energy is:
[math]\displaystyle{ U_n = \frac{n!^2}{2n} \pi \mu_0 \ell N^2 I^2 . }[/math]
Here, [math]\displaystyle{ \mu_0 }[/math] is the permeability of free space, [math]\displaystyle{ \ell }[/math] is the effective length of the magnet (the length of the magnet, including the fringing fields), [math]\displaystyle{ N }[/math] is the number of turns in one of the coils (such that the entire device has [math]\displaystyle{ 2nN }[/math] turns), and [math]\displaystyle{ I }[/math] is the current flowing in the coils. Formulating the energy in terms of [math]\displaystyle{ NI }[/math] can be useful, since the magnitude of the field and the bore radius do not need to be measured.
Note that for a non-electromagnet, this equation still holds if the magnetic excitation can be expressed in Amperes.
Derivation
The equation for stored energy in an arbitrary magnetic field is:[3]
[math]\displaystyle{ U = \frac{1}{2}\int \left(\frac{B^2}{\mu_0} \right)\,d\tau. }[/math]
Here, [math]\displaystyle{ \mu_0 }[/math] is the permeability of free space, [math]\displaystyle{ B }[/math] is the magnitude of the field, and [math]\displaystyle{ d\tau }[/math] is an infinitesimal element of volume. Now for an electromagnet with a cylindrical bore of radius [math]\displaystyle{ R }[/math], producing a pure multipole field of order [math]\displaystyle{ n }[/math], this integral becomes:
[math]\displaystyle{ U_{n} = \frac{1}{2\mu_0} \int^\ell\int^R_0\int^{2\pi}_0 B^2 \,d\tau. }[/math]
Ampere's Law for multipole electromagnets gives the field within the bore as:[4]
[math]\displaystyle{ B(r) = \frac{n!\mu_0 NI}{R^n} r^{n-1}. }[/math]
Here, [math]\displaystyle{ r }[/math] is the radial coordinate. It can be seen that along [math]\displaystyle{ r }[/math] the field of a dipole is constant, the field of a quadrupole magnet is linearly increasing (i.e. has a constant gradient), and the field of a sextupole magnet is parabolically increasing (i.e. has a constant second derivative). Substituting this equation into the previous equation for [math]\displaystyle{ U_{n} }[/math] gives:
[math]\displaystyle{ U_{n} = \frac{1}{2\mu_0} \int^\ell\int^R_0\int^{2\pi}_0 \left(\frac{n!\mu_0NI}{R^n}r^{n-1}\right)^2 \,d\tau, }[/math]
[math]\displaystyle{ U_{n} = \frac{1}{2\mu_0} \int^R_0 \left(\frac{n!\mu_0NI}{R^n}r^{n-1}\right)^2 (2\pi\ell r\,dr), }[/math]
[math]\displaystyle{ U_{n} = \frac{\pi\mu_0\ell n!^2 N^2 I^2}{R^{2n}} \int^R_0 r^{2n-1}\,dr, }[/math]
[math]\displaystyle{ U_{n} = \frac{\pi\mu_0\ell n!^2 N^2 I^2}{R^{2n}} \left( \frac{R^{2n}}{2n} \right), }[/math]
[math]\displaystyle{ U_{n} = \frac{n!^2}{2n} \pi\mu_0\ell N^2 I^2. }[/math]
References
- ↑ "Varna 2010 | the CERN Accelerator School". http://cas.web.cern.ch/cas/Bulgaria-2010/Talks-web/Brandt-1-web.pdf.
- ↑ "Wolski, Maxwell's Equations for Magnets – CERN Accelerator School 2009". https://cds.cern.ch/record/1333874?ln=de.
- ↑ Griffiths, David (2013). Introduction to Electromagnetism (4th ed.). Illinois: Pearson. p. 329.
- ↑ Tanabe, Jack (2005). Iron Dominated Electromagnets - Design, Fabrication, Assembly and Measurements (4th ed.). Singapore: World Scientific.
 |