Physics:Nuclear Overhauser effect

From HandWiki
Short description: Nuclear magnetic resonance spectroscopy effect

The nuclear Overhauser effect (NOE) is the transfer of nuclear spin polarization from one population of spin-active nuclei (e.g. 1H, 13C, 15N etc.) to another via cross-relaxation. A phenomenological definition of the NOE in nuclear magnetic resonance spectroscopy (NMR) is the change in the integrated intensity (positive or negative) of one NMR resonance that occurs when another is saturated by irradiation with an RF field. The change in resonance intensity of a nucleus is a consequence of the nucleus being close in space to those directly affected by the RF perturbation.

The NOE is particularly important in the assignment of NMR resonances, and the elucidation and confirmation of the structures or configurations of organic and biological molecules. The 1H two-dimensional NOE spectroscopy (NOESY) experiment and its extensions are important tools to identify stereochemistry of proteins and other biomolecules in solution, whereas in solid form crystal x-ray diffraction typically used to identify stereochemistry.[1] [2] [3] The heteronuclear NOE is particularly important in 13C NMR spectroscopy to identify carbons bonded to protons, to provide polarization enhancements to such carbons to increase signal-to-noise, and to ascertain the extent the relaxation of these carbons is controlled by the dipole-dipole relaxation mechanism.[4]

History

The NOE developed from the theoretical work of American physicist Albert Overhauser who in 1953 proposed that nuclear spin polarization could be enhanced by the microwave irradiation of the conduction electrons in certain metals.[5] The electron-nuclear enhancement predicted by Overhauser was experimentally demonstrated in 7Li metal by T. R. Carver and C. P. Slichter also in 1953. [6] A general theoretical basis and experimental observation of an Overhauser effect involving only nuclear spins in the HF molecule was published by Ionel Solomon in 1955.[7] Another early experimental observation of the NOE was used by Kaiser in 1963 to show how the NOE may be used to determine the relative signs of scalar coupling constants, and to assign spectral lines in NMR spectra to transitions between energy levels. In this study, the resonance of one population of protons (1H) in an organic molecule was enhanced when a second distinct population of protons in the same organic molecule was saturated by RF irradiation.[8] The application of the NOE was used by Anet and Bourn in 1965 to confirm the assignments of the NMR resonances for β,β-dimethylacrylic acid and dimethyl formamide, thereby showing that conformation and configuration information about organic molecules in solution can be obtained. [9] Bell and Saunders reported direct correlation between NOE enhancements and internuclear distances in 1970 [10] while quantitative measurements of internuclear distances in molecules with three or more spins was reported by Schirmer et al. [11]

Richard R. Ernst was awarded the 1991 Nobel Prize in Chemistry for developing Fourier transform and two-dimensional NMR spectroscopy, which was soon adapted to the measurement of the NOE, particularly in large biological molecules.[12] In 2002, Kurt Wuthrich won the Nobel Prize in Chemistry for the development of nuclear magnetic resonance spectroscopy for determining the three-dimensional structure of biological macromolecules in solution, demonstrating how the 2D NOE method (NOESY) can be used to constrain the three-dimensional structures of large biological macromolecules.[13] Professor Anil Kumar was the first to apply the two-dimensional Nuclear Overhauser Effect (2D-NOE now known as NOESY) experiment to a biomolecule, which opened the field for the determination of three-dimensional structures of biomolecules in solution by NMR spectroscopy.[14]

Relaxation

Nuclear spin energy level diagram for two spin ​1⁄2 nuclei.[3]
Steady-state pulse sequence for 1H NOE experiments

The NOE and nuclear spin-lattice relaxation are closely related phenomena. For a single spin-​1⁄2 nucleus in a magnetic field there are two energy levels that are often labeled α and β, which correspond to the two possible spin quantum states, +​1⁄2 and -​1⁄2, respectively. At thermal equilibrium, the population of the two energy levels is determined by the Boltzmann distribution with spin populations given by Pα and Pβ. If the spin populations are perturbed by an appropriate RF field at the transition energy frequency, the spin populations return to thermal equilibrium by a process called spin-lattice relaxation. The rate of transitions from α to β is proportional to the population of state α, Pα, and is a first order process with rate constant W. The condition where the spin populations are equalized by continuous RF irradiation (Pα = Pβ) is called saturation and the resonance disappears since transition probabilities depend on the population difference between the energy levels.

In the simplest case where the NOE is relevant, the resonances of two spin-​1⁄2 nuclei, I and S, are chemically shifted but not J-coupled. The energy diagram for such a system has four energy levels that depend on the spin-states of I and S corresponding to αα, αβ, βα, and ββ, respectively. The W's are the probabilities per unit time that a transition will occur between the four energy levels, or in other terms the rate at which the corresponding spin flips occur. There are two single quantum transitions, W1I, corresponding to αα ➞ βα and αβ ➞ ββ; W1S, corresponding to αα ➞ αβ and βα ➞ ββ; a zero quantum transition, W0, corresponding to βα ➞ αβ, and a double quantum transition corresponding to αα ➞ ββ.

While rf irradiation can only induce single-quantum transitions (due to so-called quantum mechanical selection rules) giving rise to observable spectral lines, dipolar relaxation may take place through any of the pathways. The dipolar mechanism is the only common relaxation mechanism that can cause transitions in which more than one spin flips. Specifically, the dipolar relaxation mechanism gives rise to transitions between the αα and ββ states (W2) and between the αβ and the βα states (W0).

Expressed in terms of their bulk NMR magnetizations, the experimentally observed steady-state NOE for nucleus I when the resonance of nucleus S is saturated ([math]\displaystyle{ M_{S} = 0 }[/math]) is defined by the expression:

[math]\displaystyle{ \eta_{I}^{S} = \left(\frac{M_{I}^{S}-M_{0I}}{M_{0I}}\right) }[/math]

where [math]\displaystyle{ M_{0I} }[/math] is the magnetization (resonance intensity) of nucleus [math]\displaystyle{ I }[/math] at thermal equilibrium. An analytical expression for the NOE can be obtained by considering all the relaxation pathways and applying the Solomon equations to obtain

[math]\displaystyle{ \eta_{I}^{S}=\frac{M_{I}^{S}-M_{0I}}{M_{0I}} = \frac{\gamma_S }{\gamma_I }\frac{\sigma_{IS}}{\rho_{I}} = \frac{\gamma_S}{\gamma_I}\left(\frac{W_{2}-W_{0}}{2W_{1}^{I}+W_{0}+W_{2}}\right) }[/math]

where

[math]\displaystyle{ \rho_{I} = 2W_{1}^{I}+W_{0}+W_{2} }[/math] and [math]\displaystyle{ \sigma_{IS} = W_{2} - W_{0} }[/math].

[math]\displaystyle{ \rho_{I} }[/math] is the total longitudinal dipolar relaxation rate ([math]\displaystyle{ 1/T_{1} }[/math]) of spin I due to the presence of spin s, [math]\displaystyle{ \sigma_{IS} }[/math] is referred to as the cross-relaxation rate, and [math]\displaystyle{ \gamma_{I} }[/math] and [math]\displaystyle{ \gamma_{S} }[/math] are the magnetogyric ratios characteristic of the [math]\displaystyle{ I }[/math] and [math]\displaystyle{ S }[/math] nuclei, respectively.

Saturation of the degenerate W1S transitions disturbs the equilibrium populations so that Pαα = Pαβ and Pβα = Pββ. The system's relaxation pathways, however, remain active and act to re-establish an equilibrium, except that the W1S transitions are irrelevant because the population differences across these transitions are fixed by the RF irradiation while the population difference between the WI transitions does not change from their equilibrium values. This means that if only the single quantum transitions were active as relaxation pathways, saturating the [math]\displaystyle{ S }[/math] resonance would not affect the intensity of the [math]\displaystyle{ I }[/math] resonance. Therefore to observe an NOE on the resonance intensity of I, the contribution of [math]\displaystyle{ W_{0} }[/math] and [math]\displaystyle{ W_{2} }[/math] must be important. These pathways, known as cross-relaxation pathways, only make a significant contribution to the spin-lattice relaxation when the relaxation is dominated by dipole-dipole or scalar coupling interactions, but the scalar interaction is rarely important and is assumed to be negligible. In the homonuclear case where [math]\displaystyle{ \gamma_{I} = \gamma_{S} }[/math], if [math]\displaystyle{ W_{2} }[/math] is the dominant relaxation pathway, then saturating [math]\displaystyle{ S }[/math] increases the intensity of the [math]\displaystyle{ I }[/math] resonance and the NOE is positive, whereas if [math]\displaystyle{ W_0 }[/math] is the dominant relaxation pathway, saturating [math]\displaystyle{ S }[/math] decreases the intensity of the [math]\displaystyle{ I }[/math] resonance and the NOE is negative.

Molecular motion

Whether the NOE is positive or negative depends sensitively on the degree of rotational molecular motion. [3] The three dipolar relaxation pathways contribute to differing extents to the spin-lattice relaxation depending a number of factors. A key one is that the balance between ω2, ω1 and ω0 depends crucially on molecular rotational correlation time, [math]\displaystyle{ \tau_{c} }[/math], the time it takes a molecule to rotate one radian. NMR theory shows that the transition probabilities are related to [math]\displaystyle{ \tau_{c} }[/math] and the Larmor precession frequencies, [math]\displaystyle{ \omega }[/math], by the relations:

[math]\displaystyle{ W_{1}^{I} \propto \frac {3\tau_c }{(1+\omega_{I}^2\tau_{c}^2)} \frac {1}{r^{6}} }[/math]
[math]\displaystyle{ W_{0} \propto \frac {2\tau_c }{(1+(\omega_{I}-\omega_S)^2\tau_{c}^2)} \frac {1}{r^{6}} }[/math]
[math]\displaystyle{ W_{2} \propto \frac {12\tau_c }{(1+(\omega_{I}+\omega_S)^2\tau_{c}^2)} \frac {1}{r^{6}} }[/math]

where [math]\displaystyle{ r }[/math] is the distance separating two spin-​1⁄2 nuclei. For relaxation to occur, the frequency of molecular tumbling must match the Larmor frequency of the nucleus. In mobile solvents, molecular tumbling motion is much faster than [math]\displaystyle{ \omega }[/math]. The so-called extreme-narrowing limit where [math]\displaystyle{ \omega\tau_{c} \ll 1 }[/math]). Under these conditions the double-quantum relaxation W2 is more effective than W1 or W0, because τc and 2ω0 match better than τc and ω1. When ω2 is the dominant relaxation process, a positive NOE results.

[math]\displaystyle{ W_{1}^{I} \propto \gamma_{I}^{2}\gamma_{S}^{2}\frac {3\tau_{c}}{r^{6} } }[/math]
[math]\displaystyle{ W_{0} \propto \gamma_{I}^{2}\gamma_{S}^{2}\frac {2\tau_{c}}{r^{6} } }[/math]
[math]\displaystyle{ W_{2}\propto \gamma_{I}^{2}\gamma_{S}^{2}\frac {12\tau_{c}}{r^{6} } }[/math]
[math]\displaystyle{ \eta_{I}^{S}(max) = \frac{\gamma_S }{\gamma_I }\left[\frac { \frac {12\tau_{c}}{r^{6}} - \frac{2\tau_{c}}{r^{6}} } { \frac {2\tau_{c}}{r^{6}} + 2\frac{3\tau_{c}}{r^{6}} + \frac {12\tau_{c}}{r^{6}} } \right] =\frac{\gamma_S }{\gamma_I }\left[ \frac {12-2 }{2+6+12 } \right] = \frac{\gamma_S }{\gamma_I }\frac{1}{2} }[/math]

This expression shows that for the homonuclear case where I = S, most notably for 1H NMR, the maximum NOE that can be observed is 1\2 irrespective of the proximity of the nuclei. In the heteronuclear case where I ≠ S, the maximum NOE is given by 1\2 (γS/γI), which, when observing heteronuclei under conditions of broadband proton decoupling, can produce major sensitivity improvements. The most important example in organic chemistry is observation of 13C while decoupling 1H, which also saturates the 1J resonances. The value of γS/γI is close to 4, which gives a maximum NOE enhancement of 200% yielding resonances 3 times as strong as they would be without NOE. [15] In many cases, carbon atoms have an attached proton, which causes the relaxation to be dominated by dipolar relaxation and the NOE to be near maximum. For non-protonated carbon atoms the NOE enhancement is small while for carbons that relax by relaxation mechanisms by other than dipole-dipole interactions the NOE enhancement can be significantly reduced. This is one motivation for using deuteriated solvents (e.g. CDCl3) in 13C NMR. Since deuterium relaxes by the quadrupolar mechanism, there are no cross-relaxation pathways and NOE is non-existent. Another important case is 15N, an example where the value of its magnetogyric ratio is negative. Often 15N resonances are reduced or the NOE may actually null out the resonance when 1H nuclei are decoupled. It is usually advantageous to take such spectra with pulse techniques that involve polarization transfer from protons to the 15N to minimize the negative NOE.

Structure elucidation

First NOE's reported by Anet and Bourne [9]

While the relationship of the steady-state NOE to internuclear distance is complex, depending on relaxation rates and molecular motion, in many instances for small rapidly tumbling molecules in the extreme-narrowing limit, the semiquantitative nature of positive NOE's is useful for many structural applications often in combination with the measurement of J-coupling constants. For example, NOE enhancements can be used to confirm NMR resonance assignments, distinguish between structural isomers, identify aromatic ring substitution patterns and aliphatic substituent configurations, and determine conformational preferences.[3]

Nevertheless, the inter-atomic distances derived from the observed NOE can often help to confirm the three-dimensional structure of a molecule.[3][15] In this application, the NOE differs from the application of J-coupling in that the NOE occurs through space, not through chemical bonds. Thus, atoms that are in close proximity to each other can give a NOE, whereas spin coupling is observed only when the atoms are connected by 2–3 chemical bonds. However, the relation ηIS(max)=​1⁄2 obscures how the NOE is related to internuclear distances because it applies only for the idealized case where the relaxation is 100% dominated by dipole-dipole interactions between two nuclei I and S. In practice, the value of ρI contains contributions from other competing mechanisms, which serve only to reduce the influence of W0 and W2 by increasing W1. Sometimes, for example, relaxation due to electron-nuclear interactions with dissolved oxygen or paramagnetic metal ion impurities in the solvent can prohibit the observation of weak NOE enhancements. The observed NOE in the presence of other relaxation mechanisms is given by

[math]\displaystyle{ \eta_{I} = \frac {\sigma_{IS}} {\rho_{I}+\rho^{*}} }[/math]

where ρ⋇ is the additional contribution to the total relaxation rate from relaxation mechanisms not involving cross relaxation. Using the same idealized two-spin model for dipolar relaxation in the extreme narrowing limit:

[math]\displaystyle{ \rho_{I} \propto \frac {\tau_{c}} {r^{6}} }[/math]

It is easy to show [15] that

[math]\displaystyle{ \eta_{I}^{S} \propto \left( \frac {\tau_{c}} {\rho^{*}} \right)\frac {1}{r^{6}} }[/math]

Thus, the two-spin steady-state NOE depends on internuclear distance only when there is a contribution from external relaxation. Bell and Saunders showed that following strict assumptions ρ⋇/τc is nearly constant for similar molecules in the extreme narrowing limit.[10] Therefore, taking ratio's of steady-state NOE values can give relative values for the internuclear distance r. While the steady-state experiment is useful in many cases, it can only provide information on relative internuclear distances. On the other hand, the initial rate at which the NOE grows is proportional to rIS−6, which provides other more sophisticated alternatives for obtaining structural information via transient experiments such as 2D-NOESY.

Two-dimensional NMR

Pulse sequence for the standard two-dimensional NOESY experiment
2D NOESY spectrum of codeine

The motivations for using two-dimensional NMR for measuring NOE's are similar as for other 2-D methods. The maximum resolution is improved by spreading the affected resonances over two dimensions, therefore more peaks are resolved, larger molecules can be observed and more NOE's can be observed in a single measurement. More importantly, when the molecular motion is in the intermediate or slow motional regimes when the NOE is either zero or negative, the steady-state NOE experiment fails to give results that can be related to internuclear distances.[3]

Codeine molecule

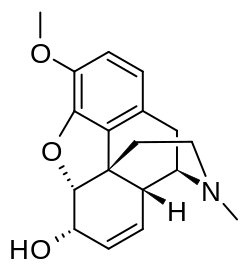
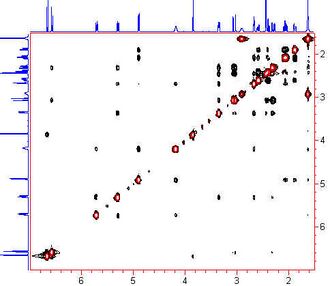
Nuclear Overhauser Effect Spectroscopy (NOESY) is a 2D NMR spectroscopic method used to identify nuclear spins undergoing cross-relaxation and to measure their cross-relaxation rates. Since 1H dipole-dipole couplings provide the primary means of cross-relaxation for organic molecules in solution, spins undergoing cross-relaxation are those close to one another in space. Therefore, the cross peaks of a NOESY spectrum indicate which protons are close to each other in space. In this respect, the NOESY experiment differs from the COSY experiment that relies on J-coupling to provide spin-spin correlation, and whose cross peaks indicate which 1H's are close to which other 1H's through the chemical bonds of the molecule.

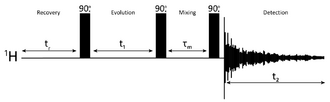
The basic NOESY sequence consists of three 90° pulses. The first pulse creates transverse spin magnetization. The spins precess during the evolution time t1, which is incremented during the course of the 2D experiment. The second pulse produces longitudinal magnetization equal to the transverse magnetization component orthogonal to the pulse direction. Thus, the idea is to produce an initial condition for the mixing period τm. During the NOE mixing time, magnetization transfer via cross-relaxation can take place. For the basic NOESY experiment, τm is kept constant throughout the 2D experiment, but chosen for the optimum cross-relaxation rate and build-up of the NOE. The third pulse creates transverse magnetization from the remaining longitudinal magnetization. Data acquisition begins immediately following the third pulse and the transverse magnetization is observed as a function of the pulse delay time t2. The NOESY spectrum is generated by a 2D Fourier transform with respect to t1 and t2. A series of experiments are carried out with increasing mixing times, and the increase in NOE enhancement is followed. The closest protons show the most rapid build-up rates of the NOE.

Inter-proton distances can be determined from unambiguously assigned, well-resolved, high signal-to-noise NOESY spectra by analysis of cross peak intensities. These may be obtained by volume integration and can be converted into estimates of interproton distances. The distance between two atoms [math]\displaystyle{ i }[/math] and [math]\displaystyle{ j }[/math] can be calculated from the cross-peak volumes [math]\displaystyle{ V }[/math] and a scaling constant [math]\displaystyle{ c }[/math]

[math]\displaystyle{ r_{\text{NOE}} = \left(\frac{c}{V_{ij}}\right)^{1/6} }[/math]

where [math]\displaystyle{ c }[/math] can be determined based on measurements of known fixed distances. The range of distances can be reported based on known distances and volumes in the spectrum, which gives a mean [math]\displaystyle{ c }[/math] and a standard deviation [math]\displaystyle{ c_{SD} }[/math], a measurement of multiple regions in the NOESY spectrum showing no peaks, i.e. noise [math]\displaystyle{ V_{\rm err} }[/math], and a measurement error [math]\displaystyle{ m_v }[/math]. The parameter [math]\displaystyle{ x }[/math] is set so that all known distances are within the error bounds. This shows that the lower range of the NOESY volume can be shown

[math]\displaystyle{ r_{\text{NOE lower}} = \left(\frac{c-xc_{SD}}{\frac{1}{m_v}V_{ij}+V_{\rm err}}\right)^{1/6} }[/math]

and that the upper bound is

[math]\displaystyle{ r_{\text{NOE higher}} = \left(\frac{c+xc_{SD}}{\frac{1}{m_v}V_{ij}-V_{\rm err}}\right)^{1/6} }[/math]

Such fixed distances depend on the system studied. For example, locked nucleic acids have many atoms whose distance varies very little in the sugar, which allows estimation of the glycosidic torsion angles, which allowed NMR to benchmark LNA molecular dynamics predictions.[16] RNAs, however, have sugars that are much more conformationally flexible, and require wider estimations of low and high bounds.[17]

In protein structural characterization, NOEs are used to create constraints on intramolecular distances. In this method, each proton pair is considered in isolation and NOESY cross peak intensities are compared with a reference cross peak from a proton pair of fixed distance, such as a geminal methylene proton pair or aromatic ring protons. This simple approach is reasonably insensitive to the effects of spin diffusion or non-uniform correlation times and can usually lead to definition of the global fold of the protein, provided a sufficiently large number of NOEs have been identified. NOESY cross peaks can be classified as strong, medium or weak and can be translated into upper distance restraints of around 2.5, 3.5 and 5.0 Å, respectively. Such constraints can then be used in molecular mechanics optimizations to provide a picture of the solution state conformation of the protein.[18] Full structure determination relies on a variety of NMR experiments and optimization methods utilizing both chemical shift and NOESY constraints.

Heteronuclear NOE


Some experimental methods

Some examples of one and two-dimensional NMR experimental techniques exploiting the NOE include:

  • NOESY, Nuclear Overhauser effect Spectroscopy
  • HOESY, Heteronuclear Overhauser effect spectroscopy
  • ROESY, Rotational frame nuclear Overhauser effect spectroscopy
  • TRNOE, Transferred nuclear Overhauser effect
  • DPFGSE-NOE, Double pulsed field gradient spin echo NOE experiment

NOESY is the determination of the relative orientations of atoms in a molecule, for example a protein or other large biological molecule, producing a three-dimensional structure. HOESY is NOESY cross-correlation between atoms of different elements. ROESY involves spin-locking the magnetization to prevent it from going to zero, applied for molecules for which regular NOESY is not applicable. TRNOE measures the NOE between two different molecules interacting in the same solution, as in a ligand binding to a protein. [19] In a DPFGSE-NOE experiment, a transient experiment that allows for suppression of strong signals and thus detection of very small NOEs.

Examples of nuclear Overhauser effect

Nuclear Overhauser effect[20]

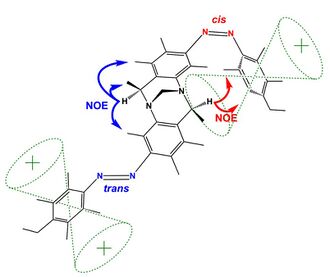
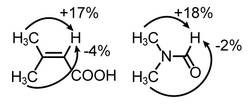
The figure (top) displays how Nuclear Overhauser Effect Spectroscopy can elucidate the structure of a switchable compound. In this example,[20] the proton designated as {H} shows two different sets of NOEs depending on the isomerization state (cis or trans) of the switchable azo groups. In the trans state proton {H} is far from the phenyl group showing blue coloured NOEs; while the cis state holds proton {H} in the vicinity of the phenyl group resulting in the emergence of new NOEs (show in red).

Another example (bottom) where application where the NOE is useful to assign resonances and determine configuration is polysaccharides. For instance, complex glucans possess a multitude of overlapping signals, especially in a proton spectrum. Therefore, it is advantageous to utilize 2D NMR experiments including NOESY for the assignment of signals. See, for example, NOE of carbohydrates.

Homonuclear NMR techniques in carbohydrate studies.

See also


References

  1. ↑ Noggle, Joseph H.; Schirmer, Roger E. (1971). The Nuclear Overhauser Effect: Chemical Applications. Academic Press. ISBN 9780125206501. https://archive.org/details/nuclearoverhause0000nogg. 
  2. ↑ Neuhaus, David; Williamson, Michael P. (2000). The Nuclear Overhauser Effect in Structural and Conformational Analysis, 2nd ed.. Wiley-VCH. 
  3. ↑ 3.0 3.1 3.2 3.3 3.4 3.5 Claridge, Timothy D.W. (2016). High Resolution NMR Techniques in Organic Chemistry, 3rd ed.. Elsevier. p. 315. ISBN 978-0080999869. 
  4. ↑ Kulhmann, Karl F.; Grant, David M.; Harris, Robin K. (1970). "Nuclear Overhauser Effects and 13C Relaxation Times in 13C {H} Double Resonance Spectra". Journal of Chemical Physics 52 (7): 3439–3448. doi:10.1063/1.1673508. 
  5. ↑ Overhauser, Albert W. (1953). "Polarization of Nuclei in Metals". Physical Review 92 (2): 411–5. doi:10.1103/PhysRev.92.411. Bibcode: 1953PhRv...92..411O. 
  6. ↑ Carver, T.R.; Slichter, C.P. (1953). "Polarization of Nuclear Spins in Metals". Physical Review 92 (1): 212–213. doi:10.1103/PhysRev.92.212.2. Bibcode: 1953PhRv...92..212C. 
  7. ↑ Solomon, I (1955). "Relaxation Processes in a System of Two Spins". Phys. Rev. 99 (2): 559. doi:10.1103/PhysRev.99.559. Bibcode: 1955PhRv...99..559S. http://www.mmrrcc.upenn.edu/mediawiki/images/d/df/A08.pdf. 
  8. ↑ Kaiser, R. (1962). "Use of the Nuclear Overhauser Effect in the Analysis of High‐Resolution Nuclear Magnetic Resonance Spectra". The Journal of Chemical Physics 39 (1): 2435–2442. doi:10.1063/1.1734045. 
  9. ↑ 9.0 9.1 Anet, F. A. L.; Bourn, A. J. R (1965). "Nuclear Magnetic Resonance Spectral Assignments from Nuclear Overhauser Effects". Journal of the American Chemical Society 87 (22): 5250–5251. doi:10.1021/ja00950a048. 
  10. ↑ 10.0 10.1 R.A., Bell; Saunders, J.K. (1970). "Correlation of the intramolecular nuclear Overhauser effect with internuclear distance". Can. J. Chem. 48 (7): 1114–1122. doi:10.1139/v70-184. 
  11. ↑ Schirmer, R.E.; Noggle, J.H.; Davis, J.P.; Hart, P.A. (1970). "Determination of molecular geometry by quantitative application of the nuclear Overhauser effect". J. Am. Chem. Soc. 92 (11): 3266–3273. doi:10.1021/ja00714a005. 
  12. ↑ "The Nobel Prize in Chemistry 1991". Nobelprize.org. http://nobelprize.org/nobel_prizes/chemistry/laureates/1991/. 
  13. ↑ "The Nobel Prize in Chemistry 2002". Nobelprize.org. http://nobelprize.org/nobel_prizes/chemistry/laureates/2002/. 
  14. ↑ Kumar, Anil; Ernst, R.R.; Wüthrich, K. (July 1980). "A two-dimensional nuclear Overhauser enhancement (2D NOE) experiment for the elucidation of complete proton-proton cross-relaxation networks in biological macromolecules". Biochemical and Biophysical Research Communications 95 (1): 1–6. doi:10.1016/0006-291X(80)90695-6. PMID 7417242. 
  15. ↑ 15.0 15.1 15.2 Derome, Andrew E. (1987). Modern NMR Techniques for Chemistry Research. Pergamon. p. 106. ISBN 978-0080325149. https://archive.org/details/modernnmrtechniq00dero. 
  16. ↑ David E. Condon; Ilyas Yildirim; Scott D. Kennedy; Brendan C. Mort; Ryszard Kierzek; Douglas H. Turner (December 2013). "Optimization of an AMBER Force Field for the Artificial Nucleic Acid, LNA, and Benchmarking with NMR of L(CAAU)". J. Phys. Chem. B 118 (5): 1216–1228. doi:10.1021/jp408909t. PMID 24377321. 
  17. ↑ "Stacking in RNA: NMR of Four Tetramers Benchmark Molecular Dynamics". Journal of Chemical Theory and Computation 11 (6): 2729–2742. June 2015. doi:10.1021/ct501025q. PMID 26082675. 
  18. ↑ Braun, W.; Gō, N. (1985). "Calculation of Protein Conformations by Proton-Proton Distance Constraints A New Efficient Algorithm". J. Mol. Biol. 186 (3): 611–626. doi:10.1016/0022-2836(85)90134-2. PMID 2419572. 
  19. ↑ Ni, Feng; Scheraga, Harold A. (1994). "Use of the Transferred Nuclear Overhauser Effect To Determine the Conformations of Ligands Bound to Proteins". Accounts of Chemical Research 27 (9): 257–264. doi:10.1021/ar00045a001. ISSN 0001-4842. 
  20. ↑ 20.0 20.1 M. Kazem-Rostami, N. G. Akhmedov and S. Faramarzi (2019). "Molecular lambda shape light-driven dual switches: spectroscopic and computational studies of the photoisomerization of bisazo Tröger base analogs". Journal of Molecular Structure 1178: 538–543. doi:10.1016/j.molstruc.2018.10.071. Bibcode: 2019JMoSt1178..538K. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Nuclear_Overhauser_effect&oldid=3279804"