Physics:Paraxial approximation

Short description: Small angle approximation in geometric optics

The error associated with the paraxial approximation. In this plot the cosine is approximated by 1 - θ²/2.

In geometric optics, the paraxial approximation is a small-angle approximation used in Gaussian optics and ray tracing of light through an optical system (such as a lens).

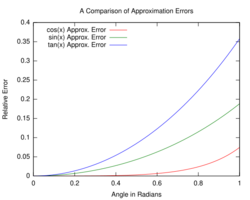
A paraxial ray is a ray which makes a small angle (θ) to the optical axis of the system, and lies close to the axis throughout the system. Generally, this allows three important approximations (for θ in radians) for calculation of the ray's path, namely:

[math]\displaystyle{ \sin \theta \approx \theta,\quad \tan \theta \approx \theta \quad \text{and}\quad\cos \theta \approx 1. }[/math]

The paraxial approximation is used in Gaussian optics and first-order ray tracing. Ray transfer matrix analysis is one method that uses the approximation.

In some cases, the second-order approximation is also called "paraxial". The approximations above for sine and tangent do not change for the "second-order" paraxial approximation (the second term in their Taylor series expansion is zero), while for cosine the second order approximation is

[math]\displaystyle{ \cos \theta \approx 1 - { \theta^2 \over 2 } \ . }[/math]

The second-order approximation is accurate within 0.5% for angles under about 10°, but its inaccuracy grows significantly for larger angles.

For larger angles it is often necessary to distinguish between meridional rays, which lie in a plane containing the optical axis, and sagittal rays, which do not.

External links

• Paraxial Approximation and the Mirror by David Schurig, The Wolfram Demonstrations Project.