Physics:Photoacoustic Doppler effect
The photoacoustic Doppler effect is a type of Doppler effect that occurs when an intensity modulated light wave induces a photoacoustic wave on moving particles with a specific frequency. The observed frequency shift is a good indicator of the velocity of the illuminated moving particles. A potential biomedical application is measuring blood flow. Specifically, when an intensity modulated light wave is exerted on a localized medium, the resulting heat can induce an alternating and localized pressure change. This periodic pressure change generates an acoustic wave with a specific frequency. Among various factors that determine this frequency, the velocity of the heated area and thus the moving particles in this area can induce a frequency shift proportional to the relative motion. Thus, from the perspective of an observer, the observed frequency shift can be used to derive the velocity of illuminated moving particles.[1]
Theory
To be simple, consider a clear medium firstly. The medium contains small optical absorbers moving with velocity vector [math]\displaystyle{ \vec{v} }[/math]. The absorbers are irradiated by a laser with intensity modulated at frequency [math]\displaystyle{ f_{0} }[/math]. Thus, the intensity of the laser could be described by:
[math]\displaystyle{ I={I }_{0 } \left[ 1+cos \left ( 2 \pi f_{0}t \right ) \right ] /2 }[/math][2]
When [math]\displaystyle{ \vec{v} }[/math] is zero, an acoustic wave with the same frequency [math]\displaystyle{ f_{0} }[/math] as the light intensity wave is induced. Otherwise, there is a frequency shift in the induced acoustic wave. The magnitude of the frequency shift depends on the relative velocity [math]\displaystyle{ \vec{v} }[/math], the angle [math]\displaystyle{ \alpha }[/math] between the velocity and the photon density wave propagation direction, and the angle [math]\displaystyle{ \theta }[/math] between the velocity and the ultrasonic wave propagation direction. The frequency shift is given by:
[math]\displaystyle{ f_{PAD}=-f_{0} \frac{ v}{ c_{0}} cos \alpha +f_{0} \frac{v}{c_{a}} cos \theta }[/math][2]
Where [math]\displaystyle{ c_{0} }[/math] is the speed of light in the medium and [math]\displaystyle{ c_{a} }[/math] is the speed of sound. The first term on the right side of the expression represents the frequency shift in the photon density wave observed by the absorber acting as a moving receiver. The second term represents the frequency shift in the photoacoustic wave due to the motion of the absorbers observed by the ultrasonic transducer.[2]
In practice, since [math]\displaystyle{ \frac{c_{0}}{c_{a}}\sim 10^{5} }[/math] and [math]\displaystyle{ v \ll c_{a} }[/math], only the second term is detectable. Therefore, the above equation reduces to:
[math]\displaystyle{ f_{PAD}= f_{0} \frac{v}{c_{a}} cos \theta = \frac{v}{\lambda} cos \theta }[/math][2][3]
In this approximation, the frequency shift is not affected by the direction of the optical radiation. It is only affected by the magnitude of velocity and the angle between the velocity and the acoustic wave propagation direction.[2]
This equation also holds for a scattering medium. In this case, the photon density wave becomes diffusive due to light scattering. Although the diffusive photon density wave has a slower phase velocity than the speed of light, its wavelength is still much longer than the acoustic wave.[3]
Experiment
In the first demonstration of the Photoacoustic Doppler effect, a continuous wave diode laser was used in a photoacoustic microscopy setup with an ultrasonic transducer as the detector. The sample was a solution of absorbing particles moving through a tube. The tube was in a water bath containing scattering particles[2]
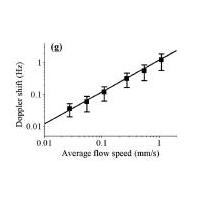
Figure 2 shows a relationship between average flow velocity and the experimental photoacoustic Doppler frequency shift. In a scattering medium, such as the experimental phantom, fewer photons reach the absorbers than in an optically clear medium. This affects the signal intensity but not the magnitude of the frequency shift. Another demonstrated feature of this technique is that it is capable of measuring flow direction relative to the detector based on the sign of the frequency shift.[2] The reported minimum detected flow rate is 0.027 mm/s in the scattering medium.[3]
Application
One promising application is the non-invasive measurement of flow. This is related to an important problem in medicine: the measurement of blood flow through arteries, capillaries, and veins.[3] Measuring blood velocity in capillaries is an important component to clinically determining how much oxygen is delivered to tissues and is potentially important to the diagnosis of a variety of diseases including diabetes and cancer. However, a particular difficulty of measuring flow velocity in capillaries is caused by the low blood flow rate and micrometre-scale diameter. Photoacoustic Doppler effect based imaging is a promising method for blood flow measurement in capillaries.
Existing techniques
Based on either ultrasound or light there are several techniques currently being used to measure blood velocity in a clinical setting or other types of flow velocities.
Doppler ultrasound
The Doppler ultrasound technique uses Doppler frequency shifts in ultrasound wave. This technique is currently used in biomedicine to measure blood flow in arteries and veins. It is limited to high flow rates ([math]\displaystyle{ \gt 1 }[/math]cm/s) generally found in large vessels due to the high background ultrasound signal from biological tissue.[3]
Laser doppler flowmetry
Laser Doppler Flowmetry utilizes light instead of ultrasound to detect flow velocity. The much shorter optical wavelength means this technology is able to detect low flow velocities out of the range of Doppler ultrasound. But this technique is limited by high background noise and low signal due to multiple scattering. Laser Doppler flowmetry can measure only the averaged blood speed within 1mm3 without information about flow direction.[3] Wideband laser Doppler imaging by digital holography with a high-speed camera can overcome some of the limitations of laser Doppler flowmetry and achieve blood flow measurements in superficial vessels at higher spatial and temporal resolution.
Doppler optical coherence tomography
Doppler Optical coherence tomography is an optical flow measurement technique that improves on the spatial resolution of laser Doppler flowmetry by rejecting multiple scattering light with coherent gating. This technique is able to detect flow velocity as low as [math]\displaystyle{ 100 \mu }[/math]m/s with the spatial resolution of [math]\displaystyle{ 5\times 5\times 15\mu }[/math]m[math]\displaystyle{ ^{3} }[/math]. The detection depth is usually limited by the high optical scattering coefficient of biological tissue to [math]\displaystyle{ \lt 1 }[/math]mm.[3]
Photoacoustic doppler flowmetry
Photoacoustic Doppler effect can be used to measure the blood flow velocity with the advantages of Photoacoustic imaging. Photoacoustic imaging combines the spatial resolution of ultrasound imaging with the contrast of optical absorption in deep biological tissue.[1] Ultrasound has good spatial resolution in deep biological tissue since ultrasonic scattering is much weaker than optical scattering, but it is insensitive to biochemical properties. Conversely, optical imaging is able to achieve high contrast in biological tissue via high sensitivity to small molecular optical absorbers, such as hemoglobin found in red blood cells, but its spatial resolution is compromised by the strong scattering of light in biological tissue. By combining the optical imaging with ultrasound, it is possible to achieve both high contrast and spatial resolution.[1]
The photoacoustic Doppler flowmetry could use the power of photoacoustics to measure flow velocities that are usually inaccessible to pure light-based or ultrasound techniques. The high spatial resolution could make it possible to pinpoint only a few absorbing particles localized to a single capillary. High contrast from the strong optical absorbers make it possible to clearly resolve the signal from the absorbers over the background.
See also
- Photoacoustic spectroscopy
- Photoacoustic imaging in biomedicine
- Photoacoustic tomography
- Doppler effect
- laser Doppler imaging
- Doppler optical coherence tomography
References
- ↑ 1.0 1.1 1.2 LV Wang; HI Wu (2007). Biomedical Optics: Principles and Imaging. Wiley. ISBN 978-0-471-74304-0.
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 H. Fang, K. Maslov, L.V. Wang. "Photoacoustic Doppler Effect from Flowing Small Light-Absorbing Particles." Physical Review Letters 99, 184501 (2007)
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 3.7 H. Fang, K. Maslov, L.V. Wang. "Photoacoustic Doppler flow measurement in optically scattering media." Applied Physics Letters 91 (2007) 264103
 |  |
