Physics:Photoemission orbital tomography

In physics and chemistry, photoemission orbital tomography (POT; sometimes called photoemission tomography) is a combined experimental / theoretical approach which reveals information about the spatial distribution of individual molecular orbitals. Experimentally, it uses angle-resolved photoemission spectroscopy (ARPES) to obtain constant binding energy photoemission angular distribution maps, so-called tomograms (also known as momentum maps or [math]\displaystyle{ k }[/math]-maps), to reveal information about the electron probability distribution in molecular orbitals. Theoretically, one rationalizes these tomograms as hemispherical cuts through the molecular orbital in momentum space. This interpretation relies on the assumption of a plane wave final state, i.e., the idea that the outgoing electron can be treated as a free electron, which can be further exploited to reconstruct real-space images of molecular orbitals on a sub-Ångström length scale in two or three dimensions. Presently, POT has been applied to various organic molecules forming well-oriented monolayers on single crystal surfaces or to two-dimensional materials.

Theory

A molecular orbital is transformed from real space to momentum space via a discrete Fourier transform. By taking a hemispherical cut, one obtains a so-called momentum map which corresponds to an intensity map of the photoelectron angular distribution

Within the framework of POT, the photo-excitation is treated as a single coherent process from an initial (molecular) orbital [math]\displaystyle{ \Psi_i }[/math] to the final state [math]\displaystyle{ \Psi_f }[/math], which is referred to as the one-step-model of photoemission. The intensity distribution in the tomograms, [math]\displaystyle{ I(k_x,k_y;E_\mathrm{kin}) }[/math], is then given from Fermi's golden rule as

[math]\displaystyle{ I(k_x,k_y;E_\mathrm{kin}) \propto \left| \langle \Psi_f(k_x,k_y;E_\mathrm{kin}) | \vec{A} \cdot \vec{p} | \Psi_i \rangle \right|^2 \times \delta \left(E_i + \Phi + E_\mathrm{kin} - \hbar \omega \right). }[/math]

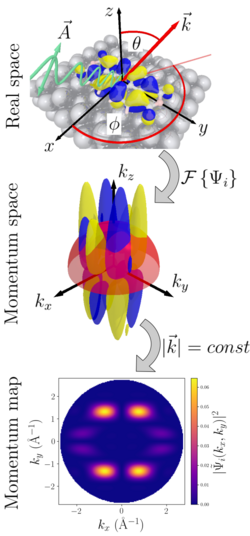
Here, [math]\displaystyle{ k_x }[/math] and [math]\displaystyle{ k_y }[/math] are the components of the emitted electron's wave vector parallel to the surface, which are related to the polar and azimuthal emission angles [math]\displaystyle{ \theta }[/math] and [math]\displaystyle{ \phi }[/math] defined in the figure as follows,

[math]\displaystyle{ k_x = k \sin \theta \cos \phi }[/math]

[math]\displaystyle{ k_y = k \sin \theta \sin \phi }[/math]

where [math]\displaystyle{ k }[/math] and [math]\displaystyle{ E_\mathrm{kin} = \frac{\hbar^2 k^2}{2m} }[/math] are the wave number and kinetic energy of the emitted electron, respectively, where [math]\displaystyle{ \hbar }[/math] is the reduced Planck constant and [math]\displaystyle{ m }[/math] is the electron mass. The transition matrix element is given in the dipole approximation, where [math]\displaystyle{ \vec{p} }[/math] and [math]\displaystyle{ \vec{A} }[/math], respectively, denote the momentum operator of the electron and the vector potential of the exciting electromagnetic wave. In the independent electron approximation, the spectral function reduces to a delta function and ensures energy conservation, where [math]\displaystyle{ \Phi }[/math] denotes the sample work function, [math]\displaystyle{ E_i }[/math] the binding energy of the initial state, and [math]\displaystyle{ \hbar \omega }[/math] the energy of the exciting photon.

In POT, the evaluation of the transition matrix element is further simplified by approximating the final state by a plane wave. Then, the photocurrent [math]\displaystyle{ I_i }[/math] arising from one particular initial state [math]\displaystyle{ i }[/math] is proportional to the Fourier transform [math]\displaystyle{ \tilde{\Psi}_{i} (\vec{k}) = \mathcal{F}\left\{ \Psi_i(\vec{r}) \right\} }[/math] of the initial state wave function modulated by the weakly angle-dependent polarization factor [math]\displaystyle{ \vec{A} \cdot \vec{k} }[/math]:

[math]\displaystyle{ I_i(k_x,k_y) \propto \left|\vec{A} \cdot \vec{k}\right|^2 \cdot \left| \tilde{\Psi}_{i} (k_x, k_y) \right|^2 \quad \textrm{with} \quad |\vec{k}|^2 = k_x^2 + k_y^2 + k_z^2 = \frac{2m}{\hbar^2} E_\mathrm{kin} }[/math]

As illustrated in the figure, the relationship between the real space orbital and its photoemission distribution can be represented by an Ewald's sphere-like construction. Thus, a one-to-one relation between the photocurrent and the molecular orbital density in reciprocal space can be established. Moreover, a reconstruction of molecular orbital densities in real space via an inverse Fourier transform and applying an iterative phase retrieval algorithm has also been demonstrated.

Experiment

The basic experimental requirements are a reasonably monoenergetic photon source (inert gas discharge lamps, synchrotron radiation or UV laser sources) and an angle-resolved photoelectron spectrometer. Ideally, a large angular distribution ([math]\displaystyle{ k }[/math]-area) should be collected. Much of the development of POT was made using a toroidal analyzer with [math]\displaystyle{ p }[/math]-polarized synchrotron radiation. Here the spectrometer collects the hemicircle of emissions ([math]\displaystyle{ -90^\circ \lt \theta \lt +90^\circ }[/math]) in the plane of incidence and polarization, and the momentum maps are obtained by rotating the sample azimuth ([math]\displaystyle{ \phi }[/math]). A number of commercially available electron spectrometers are now on the market which have been shown to be suited to POT. These include large acceptance angle hemispherical analysers, spectrometers with photoemission electron microscopy (PEEM) lenses and time of flight (TOF) spectrometers.

Applications and future developments

Experimental momentum map for the PTCDA HOMO (top left) and its reconstructed real space distribution (top right) compared to a simulated momentum map (bottom left) computed from a DFT orbital (bottom right).

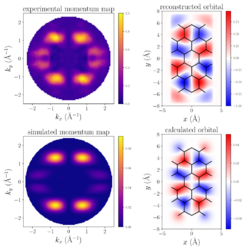
POT has found many interesting applications including the assignment of molecular orbital densities in momentum and real space, the deconvolution of spectra into individual orbital contributions beyond the limits of energy resolution, the extraction of detailed geometric information, or the identification of reaction products. Recently, the extension to the time-domain has been demonstrated by combining time-resolved photoemission using high laser harmonics and a momentum microscope to measure the full momentum-space distribution of transiently excited electrons in organic molecules.

The possibility to measure the spatial distribution of electrons in frontier molecular orbitals has stimulated discussions on the interpretation of the concept of orbitals itself. The present understanding is that the information retrieved from photoemission orbital tomography should be interpreted as Dyson orbitals.

Approximating the photoelectron's final state by a plane wave have been viewed critically. Indeed there are cases where the plane-wave final state approximation is problematic including a proper description of the photon energy dependence, the circular dichroism in the photoelectron angular distribution or certain experimental geometries. Nevertheless, the usefulness of the plane wave final state approximation has been extended beyond the originally suggested case of [math]\displaystyle{ \pi }[/math]-orbitals of large, planar [math]\displaystyle{ \pi }[/math]-conjugated molecules to three-dimensional molecules, small organic molecules and extended to two-dimensional materials. Theoretical approaches beyond the plane wave final state approximation have also been demonstrated including time-dependent density functional theory calculations or Green's function techniques.