Physics:Ewald's sphere
The Ewald sphere is a geometric construction used in electron, neutron, and x-ray diffraction which shows the relationship between:
- the wavevector of the incident and diffracted beams,
- the diffraction angle for a given reflection,
- the reciprocal lattice of the crystal.
It was conceived by Paul Peter Ewald, a German physicist and crystallographer.[1] Ewald himself spoke of the sphere of reflection.[2] It is often simplified to the two-dimensional "Ewald's circle" model or may be referred to as the Ewald sphere.
Ewald construction
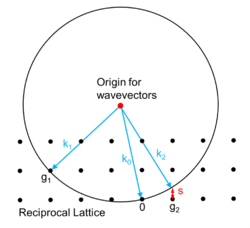
A crystal can be described as a lattice of atoms, which in turn this leads to the reciprocal lattice. With electrons, neutrons or x-rays there is diffraction by the atoms, and if there is an incident plane wave [math]\displaystyle{ \exp(2 \pi i \mathbf{k_0}\cdot \mathbf{r}) }[/math][lower-alpha 1] with a wavevector [math]\displaystyle{ \mathbf{k_0} }[/math], there will be outgoing wavevectors [math]\displaystyle{ \mathbf{k_1} }[/math] and [math]\displaystyle{ \mathbf{k_2} }[/math] as shown in the diagram[3] after the wave has been diffracted by the atoms.
The energy of the waves (electron, neutron or x-ray) depends upon the magnitude of the wavevector, so if there is no change in energy (elastic scattering) these have the same magnitude, that is they must all lie on the Ewald sphere. In the Figure the red dot is the origin for the wavevectors, the black spots are reciprocal lattice points (vectors) and shown in blue are three wavevectors. For the wavevector [math]\displaystyle{ \mathbf{k_1} }[/math] the corresponding reciprocal lattice point [math]\displaystyle{ \mathbf{g_1} }[/math] lies on the Ewald sphere, which is the condition for Bragg diffraction. For [math]\displaystyle{ \mathbf{k_2} }[/math] the corresponding reciprocal lattice point [math]\displaystyle{ \mathbf{g_2} }[/math] is off the Ewald sphere, so [math]\displaystyle{ \mathbf{k_2} = \mathbf{k_0} + \mathbf{g_2} + \mathbf{s} }[/math] where [math]\displaystyle{ \mathbf{s} }[/math] is called the excitation error. The amplitude and also intensity of diffraction into the wavevector [math]\displaystyle{ \mathbf{k_2} }[/math] depends upon the Fourier transform of the shape of the sample,[3][4] the excitation error [math]\displaystyle{ \mathbf{s} }[/math], the structure factor for the relevant reciprocal lattice vector, and also whether the scattering is weak or strong. For neutrons and x-rays the scattering is generally weak so there is mainly Bragg diffraction, but it is much stronger for electron diffraction.[3][5]
See also
References
- ↑ Ewald, P. P. (1921). "Die Berechnung optischer und elektrostatischer Gitterpotentiale". Annalen der Physik 369 (3): 253–287. doi:10.1002/andp.19213690304. Bibcode: 1921AnP...369..253E. https://zenodo.org/record/1424363.
- ↑ Ewald, P. P. (1969). "Introduction to the dynamical theory of X-ray diffraction". Acta Crystallographica Section A 25 (1): 103–108. doi:10.1107/S0567739469000155. Bibcode: 1969AcCrA..25..103E.
- ↑ 3.0 3.1 3.2 John M., Cowley (1995). Diffraction physics. Elsevier. ISBN 0-444-82218-6. OCLC 247191522. http://worldcat.org/oclc/247191522.
- ↑ Rees, A. L. G.; Spink, J. A. (1950). "The shape transform in electron diffraction by small crystals". Acta Crystallographica 3 (4): 316–317. doi:10.1107/s0365110x50000823. ISSN 0365-110X. http://dx.doi.org/10.1107/s0365110x50000823.
- ↑ Peng, L.-M.; Dudarev, S. L.; Whelan, M. J. (2011). High energy electron diffraction and microscopy. Oxford: Oxford University Press. ISBN 978-0-19-960224-7. OCLC 656767858. https://www.worldcat.org/oclc/656767858.
Notes
- ↑ In some physics texts the [math]\displaystyle{ 2 \pi }[/math] is omitted
External links
 |  |
