Physics:Pseudo Jahn–Teller effect
The pseudo Jahn–Teller effect (PJTE), occasionally also known as second-order JTE, is a direct extension of the Jahn–Teller effect (JTE) where spontaneous symmetry breaking in polyatomic systems (molecules and solids) occurs even when the relevant electronic states are not degenerate. The PJTE can occur under the influence of sufficiently low-lying electronic excited states of appropriate symmetry. "The pseudo Jahn–Teller effect is the only source of instability and distortions of high-symmetry configurations of polyatomic systems in nondegenerate states, and it contributes significantly to the instability in degenerate states".[1]
History
In their early 1957 paper on what is now called pseudo Jahn–Teller effect (PJTE), Öpik and Pryce[2] showed that a small splitting of the degenerate electronic term does not necessarily remove the instability and distortion of a polyatomic system induced by the Jahn–Teller effect (JTE), provided that the splitting is sufficiently small (the two split states remain "pseudo degenerate"), and the vibronic coupling between them is strong enough. From another perspective, the idea of a "mix" of different electronic states induced by low-symmetry vibrations was introduced in 1933 by Herzberg and Teller[3] to explore forbidden electronic transitions, and extended in the late 1950s by Murrell and Pople[4] and by Liehr.[5]
The role of excited states in softening the ground state with respect to distortions in benzene was demonstrated qualitatively by Longuet-Higgins and Salem[6] by analyzing the π electron levels in the Hückel approximation, while a general second-order perturbation formula for such vibronic softening was derived by Bader in 1960.[7] In 1961 Fulton and Gouterman[8] presented a symmetry analysis of the two-level case in dimers and introduced the term "pseudo Jahn–Teller effect". The first application of the PJTE to solving a major solid-state structural problem with regard to the origin of ferroelectricity was published in 1966 by Isaac Bersuker,[9] and the first book on the JTE covering the PJTE was published in 1972 by Englman.[10] The second-order perturbation approach was employed by Pearson in 1975 to predict instabilities and distortions in molecular systems;[11] he called it "second-order JTE" (SOJTE). The first explanation of PJT origin of puckering distortion as due to the vibronic coupling to the excited state, was given for the N3H32+ radical by Borden, Davidson, and Feller in 1980[12] (they called it "pyramidalization").
Methods of numerical calculation of the PJT vibronic coupling effect with applications to spectroscopic problems were developed in the early 1980s[13]
A significant step forward in this field was achieved in 1984 when it was shown by numerical calculations[14] that the energy gap to the active excited state may not be the ultimate limiting factor in the PJTE, as there are two other compensating parameters in the condition of instability. It was also shown that, in extension of the initial definition,[2] the PJT interacting electronic states are not necessarily components emerging from the same symmetry type (as in the split degenerate term). As a result, the applicability of the PJTE became a priory unlimited. Moreover, it was shown by Bersuker that the PJTE is the only source of instability of high-symmetry configurations of polyatomic systems in nondegenerate states (works cited in Refs.[1][15][16]), and degeneracy and pseudo degeneracy are the only source of spontaneous symmetry breaking in matter in all its forms.[17] The many applications of the PJTE to the study of a variety of properties of molecular systems and solids are reflected in a number of reviews and books [1][10][11][15][16][17][18][19]), as well as in proceedings of conferences on the JTE.
Theoretical background
General theory
The equilibrium geometry of any polyatomic system in nondegenerate states is defined as corresponding to the point of the minimum of the adiabatic potential energy surface (APES), where its first derivatives are zero and the second derivatives are positive. If we denote the energy of the system as a function of normal displacements [math]\displaystyle{ Q_\alpha }[/math] as [math]\displaystyle{ E(Q_\alpha) }[/math], at the minimum point of the APES ([math]\displaystyle{ Q_\alpha = 0 }[/math]), the curvature [math]\displaystyle{ K }[/math] of [math]\displaystyle{ E(Q_\alpha) }[/math] in direction [math]\displaystyle{ Q }[/math],
[math]\displaystyle{ K = \left(\frac{d^2E}{dQ_\alpha^2}\right)_0 }[/math] (1)
is positive, i.e., [math]\displaystyle{ K\gt 0 }[/math]. Very often the geometry of the system at this point of equilibrium on the APES does not coincide with the highest possible (or even with any high) symmetry expected from general symmetry considerations. For instance, linear molecules are bent at equilibrium, planar molecules are puckered, octahedral complexes are elongated, or compressed, or tilted, cubic crystals are tetragonally polarized (or have several structural phases), etc. The PJTE is the general driving force of all these distortions if they occur in the nondegenerate electronic states of the high-symmetry (reference) geometry. If at the reference configuration the system is structurally unstable with respect to some nuclear displacements [math]\displaystyle{ Q_\alpha }[/math], then [math]\displaystyle{ K\lt 0 }[/math] in this direction. The general formula for the energy is [math]\displaystyle{ E = \langle \psi_0 | H | \psi_0 \rangle }[/math], where [math]\displaystyle{ H }[/math] is the Hamiltonian and [math]\ce{ \psi_0 }[/math] is the wavefunction of the nondegenerate ground state. Substituting [math]\displaystyle{ E }[/math] in Eq. (1), we get (omitting the [math]\displaystyle{ \alpha }[/math] index for simplicity)[1]
[math]\displaystyle{ K = K_0 + K_v }[/math] (2)
[math]\displaystyle{ K_0 = \left\langle \psi_0 \Biggr| \left(\frac{d^2H}{dQ^2}\right)_0 \Biggr| \psi_0\right\rangle }[/math] (3)
[math]\displaystyle{ K_v = -\sum_n \frac{|\langle\psi_n|(\operatorname{d}H/\operatorname{d}Q)_0|\psi_n\rangle|^2}{E_n - E_0} }[/math] (4)
where [math]\displaystyle{ \psi_n }[/math] are the wavefunctions of the excited states, and the [math]\displaystyle{ K_v }[/math] expression, obtained as a second order perturbation correction, is always negative, [math]\displaystyle{ K_v \lt 0 }[/math]. Therefore, if [math]\displaystyle{ K_0 \gt 0 }[/math], the [math]\displaystyle{ K_v }[/math] contribution is the only source of instability. The matrix elements in Eq. (4) are off-diagonal vibronic coupling constants,[10][15][16]
[math]\displaystyle{ F_{0n} = \langle \psi_0 | (\operatorname{d}\!H/\operatorname{d}\!Q)_0 | \psi_n \rangle }[/math] (5)
These measure the mixing of the ground and excited states under the nuclear displacements [math]\displaystyle{ Q }[/math], and therefore [math]\displaystyle{ K_v }[/math] is termed the vibronic contribution. Together with the [math]\displaystyle{ K_0 }[/math] value and the energy gap [math]\displaystyle{ 2\Delta_{0n} = E_n - E_0 }[/math]between the mixing states, [math]\displaystyle{ F_{0n} }[/math] are the main parameters of the PJTE (see below). In a series of papers beginning in 1980 (see references in [1][15][16]) it was proved that for any polyatomic system in the high-symmetry configuration
[math]\displaystyle{ K_0 \gt 0 }[/math] (6)
and hence the vibronic contribution is the only source of instability of any polyatomic system in nondegenerate states. If [math]\displaystyle{ K_0 \gt 0 }[/math] for the high-symmetry configuration of any polyatomic system, then a negative curvature, [math]\displaystyle{ K = (K_0 + K_v) \lt 0 }[/math], can be achieved only due to the negative vibronic coupling component [math]\displaystyle{ K_v }[/math], and only if [math]\displaystyle{ |K_v| \gt K_0 }[/math]. It follows that any distortion of the high-symmetry configuration is due to, and only to the mixing of its ground state with excited electronic states by the distortive nuclear displacements realized via the vibronic coupling in Eq. (5). The latter softens the system with respect to certain nuclear displacements ([math]\displaystyle{ K_v \lt 0 }[/math]), and if this softening is larger than the original (nonvibronic) hardness [math]\displaystyle{ K_0 }[/math] in this direction, the system becomes unstable with respect to the distortions under consideration, leading to its equilibrium geometry of lower symmetry, or to dissociation. There are many cases when neither the ground state is degenerate, nor is there a significant vibronic coupling to the lowest excited states to realize PJTE instability of the high-symmetry configuration of the system, and still there is a ground state equilibrium configuration with lower symmetry. In such cases the symmetry breaking is produced by a hidden PJTE (similar to a hidden JTE); it takes place due to a strong PJTE mixing of two excited states, one of which crosses the ground state to create a new (lower) minimum of the APES with a distorted configuration.[1]
The two-level problem
The use of the second order perturbation correction, Eq. (4), for the calculation of the [math]\displaystyle{ K_v }[/math] value in the case of PJTE instability is incorrect because in this case [math]\displaystyle{ |K_v| \gt K_0 }[/math], meaning the first perturbation correction is larger than the main term, and hence the criterion of applicability of the perturbation theory in its simplest form does not hold. In this case, we should consider the contribution of the lowest excited states (that make the total curvature negative) in a pseudo degenerate problem of perturbation theory. For the simplest case when only one excited state creates the main instability of the ground state, we can treat the problem via a pseudo degenerate two-level problem, including the contribution of the higher, weaker-influencing states as a second order correction.[1] In the PJTE two-level problem we have two electronic states of the high-symmetry configuration, ground [math]\displaystyle{ \beta }[/math] and excited [math]\displaystyle{ \gamma }[/math], separated by an energy interval of [math]\displaystyle{ 2\Delta }[/math], that become mixed under nuclear displacements of certain symmetry [math]\displaystyle{ Q = Q_\alpha }[/math]; the denotations [math]\displaystyle{ \alpha }[/math], [math]\displaystyle{ \beta }[/math], and [math]\displaystyle{ \gamma }[/math] indicate, respectively, the irreducible representations to which the symmetry coordinate and the two states belong. In essence, this is the original formulation of the PJTE. Assuming that the excited state is sufficiently close to the ground one, the vibronic coupling between them should be treated as a perturbation problem for two near-degenerate states. With both interacting states non-degenerate the vibronic coupling constant [math]\displaystyle{ F }[/math] in Eq. (5) (omitting indices) is non-zero for only one coordinate [math]\displaystyle{ Q = Q_\alpha }[/math] with [math]\displaystyle{ \alpha = \beta\gamma }[/math]. This gives us directly the symmetry of the direction of softening and possible distortion of the ground state. Assuming that the primary force constants [math]\displaystyle{ K_0 }[/math] in the two states are the same (for different [math]\displaystyle{ K_0 }[/math] see [1]), we get a 2×2 secular equation with the following solution for the energies [math]\displaystyle{ \varepsilon_\pm }[/math] of the two states interacting under the linear vibronic coupling (energy is referred to the middle of the [math]\displaystyle{ 2\Delta }[/math] gap between the levels at the undistorted geometry):
[math]\displaystyle{ \varepsilon_\pm = \frac 1 2 Q^2 \pm (\Delta^2 + F^2Q^2)^{1/2} }[/math] (7)
It is seen from these expressions that, on taking into account the vibronic coupling, [math]\displaystyle{ F\neq 0 }[/math], the two APES curves change in different ways: in the upper sheet the curvature (the coefficient at [math]\displaystyle{ Q^2 }[/math] in the expansion on [math]\displaystyle{ Q }[/math]) increases, whereas in the lower one it decreases. But until [math]\displaystyle{ F^2/K_0 \lt \Delta }[/math] the minima of both states correspond to the point [math]\displaystyle{ Q=0 }[/math], as in the absence of vibronic mixing. However, if
[math]\displaystyle{ \frac{F^2}{K_0} \gt \Delta }[/math] (8)
the curvature of the lower curve of the APES becomes negative, and the system is unstable with respect to the [math]\displaystyle{ Q }[/math] displacements (Fig. 1). Under condition (8), the minima points on the APES are given by
[math]\displaystyle{ \pm Q_0 = \left(\frac{F^2}{K_0^2} - \frac{\Delta^2}{F^2}\right)^{1/2} }[/math] (9)
From these expressions and Fig. 1 it is seen that while the ground state is softened (destabilized) by the PJTE, the excited state is hardened (stabilized), and this effect is the larger, the smaller [math]\displaystyle{ \Delta }[/math] and the larger F. It takes place in any polyatomic system and influences many molecular properties, including the existence of stable excited states of molecular systems that are unstable in the ground state (e.g., excited states of intermediates of chemical reactions); in general, even in the absence of instability the PJTE softens the ground state and increases the vibrational frequencies in the excited state.
Comparison with the Jahn-Teller effect
The two branches of the APES for the case of strong PJTE resulting in the instability of the ground state (when the condition of instability (11) holds) are illustrated in Fig. 1b in comparison with the case when the two states have the same energy (Fig. 1a), i. e. when they are degenerate and the Jahn–Teller effect (JTE) takes place. We see that the two cases, degenerate and nondegenerate but close-in-energy (pseudo degenerate) are similar in generating two minima with distorted configurations, but there are important differences: while in the JTE there is a crossing of the two terms at the point of degeneracy (leading to conical intersections in more complicated cases), in the nondegenerate case with strong vibronic coupling there is an "avoided crossing" or "pseudo crossing". Even a more important difference between the two vibronic coupling effects emerges from the fact that the two interacting states in the JTE are components of the same symmetry type, whereas in the PJTE each of the two states may have any symmetry. For this reason, the possible kinds of distortion is very limited in the JTE, and unlimited in the PJTE. It is also noticeable that while the systems with JTE are limited by the condition of electron degeneracy, the applicability of the PJTE has no a priori limitations, as it includes also the cases of degeneracy. Even when the PJT coupling is weak and the inequality (11) does not hold, the PJTE is still significant in softening (lowering the corresponding vibrational frequency) of the ground state and increasing it in the excited state.[1] When considering the PJTE in an excited state, all the higher in energy states destabilize it, while the lower ones stabilize it.
File:Fig. 2 Illustration to the origin of the PJTE as due to added covalence bonding by distortion.tif For a better understanding it is important to follow up on how the PJTE is related to intramolecular interactions. In other words, what is the physical driving force of the PJTE distortions (transformations) in terms of well-known electronic structure and bonding? The driving force of the PJTE is added (improved) covalence: the PJTE distortion takes place when it results in an energy gain due to greater covalent bonding between the atoms in the distorted configuration.[1][16] Indeed, in the starting high-symmetry configuration the wavefunctions of the electronic states, ground and excited, are orthogonal by definition. When the structure is distorted, their orthogonality is violated, and a nonzero overlap between them occurs. If for two near-neighbor atoms the ground state wavefunction pertains (mainly) to one atom and the excited state wavefunction belongs (mainly) to the other, the orbital overlap resulting from the distortion adds covalency to the bond between them, so the distortion becomes energetically favorable (Fig. 2).
Applications
Examples of the PJTE being used to explain chemical, physical, biological, and materials science phenomena are innumerable; as stated above, the PJTE is the only source of instability and distortions in high-symmetry configurations of molecular systems and solids with nondegenerate states, hence any phenomenon stemming from such instability can be explained in terms of the PJTE. Below are some illustrative examples.
Linear systems
PJTE versus Renner–Teller effect in bending distortions. Linear molecules are exceptions from the JTE, and for a long time it was assumed that their bending distortions in degenerate states (observed in many molecules) is produced by the Renner–Teller effect (RTE) (the splitting of the generate state by the quadratic terms of the vibronic coupling). However, recently it was proved [1] that the RTE, by splitting the degenerate electronic state, just softens the lower branch of the APES, but this lowering of the energy is not enough to overcome the rigidity of the linear configuration and to produce bending distortions. It follows that the bending distortion of linear molecular systems is due to, and only to the PJTE that mixes the electronic state under consideration with higher in energy (excited) states. This statement is enhanced by the fact that many linear molecules in nondegenerate states (and hence with no RTE) are, too, bent in the equilibrium configuration. The physical reason for the difference between the PJTE and the RTE in influencing the degenerate term is that while in the former case the vibronic coupling with the excited state produces additional covalent bonding that makes the distorted configuration preferable (see above, section 2.3), the RTE has no such influence; the splitting of the degenerate term in the RTE takes place just because the charge distribution in the two states becomes nonequivalent under the bending distortion.
Peierls distortion in linear chains. In linear molecules with three or more atoms there may be PJTE distortions that do not violate the linearity but change the interatomic distances. For instance, as a result of the PJTE a centrosymmetric linear system may become non-centrosymmetric in the equilibrium configurations, as, for example, in the BNB molecule (see in [1]). An interesting extension of such distortions in sufficiently long (infinite) linear chains was first considered by Peierls.[20] In this case the electronic states, combinations of atomic states, are in fact band states, and it was shown that if the chain is composed by atoms with unpaired electrons, the valence band is only half filled, and the PJTE interaction between the occupied and unoccupied band states leads to the doubling of the period of the linear chain (see also in the books [15][16]).
Broken cylindrical symmetry. It was shown also that the PJTE not only produces the bending instability of linear molecules, but if the mixing electronic states involve a Δ state (a state with a nonzero momentum with respect to the axis of the molecule, its projection quantum number being Λ=2), the APES, simultaneously with the bending, becomes warped along the coordinate of rotations around the molecular axis, thus violating both the linear and cylindrical symmetry.[21] It happens because the PJTE, by mixing the wavefunctions of the two interacting states, transfers the high momentum of the electrons from states with Λ=2 to states with lower momentum, and this may alter significantly their expected rovibronic spectra.
Nonlinear molecules and two-dimensional (2D) systems
PJTE and combined PJTE plus JTE effects in molecular structures. There is a practically unlimited number of molecular systems for which the origin of their structural properties was revealed and/or rationalized based on the PJTE, or a combination of the PJTE and JTE. The latter stems from the fact that in any system with a JTE in the ground state the presence of a PJT active excited state is not excluded, and vice versa, the active excited state for the PJTE of the ground one may be degenerate, and hence JT active. Examples are shown, e.g., in Refs.,[1][10][11][15][17][18][19] including molecular systems like Na3, C3H3, C4X4 (X= H, F, Cl, Br), CO3, Si4R4 (with R as large ligands), planar cyclic CnHn, all kind of coordination systems of transition metals, mixed-valence compounds, biological systems, origin of conformations, geometry of ligands' coordination, and others. Indeed, it is difficult to find a molecular system for which the PJTE implications are a priori excluded, which is understandable in view of the mentioned above unique role of the PJTE in such instabilities. Three methods to quench the PJTE have been documented: changing the electronic charge of the molecule,[22] sandwiching the molecule with other ions and cyclic molecules,[23][24][25] and manipulating the environment of the molecule.[26]
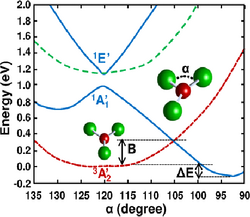
Hidden PJTE, spin crossover, and magnetic-dielectric bistability. As mentioned above, there are molecular systems in which the ground state in the high-symmetry configuration is neither degenerate to trigger the JTE, nor does it interact with the low-lying excited states to produce the PJTE (e.g., because of their different spin multiplicity). In these situations, the instability is produced by a strong PJTE in the excited states; this is termed "hidden PJTE" in the sense that its origin is not seen explicitly as a PJTE in the ground state. An interesting typical situation of hidden PJTE emerges in molecular and solid-state systems with valence half-filed closed shells electronic configurations e2 and t3. For instance, in the e2 case the ground state in the high-symmetry equilibrium geometry is an orbital non-degenerate triplet 3A, while the nearby low-lying two excited electronic states are close-in-energy singlets 1E and 1A; due to the strong PJT interaction between the latter, the lower component of 1E crosses the triplet state to produce a global minimum with lower symmetry. Fig. 3 illustrates the hidden PJTE in the CuF3 molecule, showing also the singlet-triplet spin crossover and the resulting two coexisting configurations of the molecule: high-symmetry (undistorted) spin-triplet state with a nonzero magnetic moment, and a lower in energy dipolar-distorted singlet state with zero magnetic moment. Such magnetic-dielectric bistability is inherent to a whole class of molecular systems and solids.[27]
Puckering in planar molecules and graphene-like 2D and quasi 2D systems. Special attention has been paid recently to 2D systems in view of a variety of their planar-surface-specific physical and chemical properties and possible graphene-like applications in electronics. Similar-to-graphene properties are sought for in silicene, phosphorene, boron nitride, zinc oxide, gallium nitride, as well as in 2D transition metal dichalkogenides and oxides, plus a number of other organic and inorganic 2D and quasi-2D compounds with expected similar properties. One of the main important features of these systems is their planarity or quasi-planarity, but many of the quasi-2D compounds are subject to out-of-plane deviations known as puckering (buckling). The instability and distortions of the planar configuration (as in any other systems in nondegenerate state) was shown to be due to the PJTE.[1][15][16] Detailed exploration of the PJTE in such systems allows one to identify the excited states that are responsible for the puckering, and suggest possible external influence that restores their planarity, including oxidation, reduction, substitutions, or coordination to other species.[16][28] Recent investigations have also extended to 3D compounds.[29]
Solid state and materials science
Cooperative PJTE in BaTiO3-type crystals and ferroelectricity. In crystals with PJTE centers the interaction between the local distortions may lead to their ordering to produce a phase transition to a regular crystal phase with lower symmetry. Such cooperative PJTE is quite similar to the cooperative JTE; it was shown in one of the first studies of the PJTE in solid state systems [9] that in the case of ABO3 crystals with perovskite structure the local dipolar PJTE distortions at the transition metal B center and their cooperative interactions lead to ferroelectric phase transitions. Provided the criterion for PJTE is met, each [BO6] center has an APES with eight equivalent minima along the trigonal axes, six orthorhombic, and (higher) twelve tetragonal saddle-points between them. With temperature, the gradually reached transitions between the minima via the different kind of saddle-points explains the origin of all the four phases (three ferroelectric and one paraelectric) in perovskites of the type BaTiO3 and their properties. The predicted by the theory trigonal displacement of the Ti ion in all four phases, the fully disordered PJTE distortions in the paraelectric phase, and their partially disordered state in two other phases was confirmed by a variety of experimental investigations (see in [1][9][15][16]).
Multiferroicity and magnetic-ferroelectric crossover. The PJTE theory of ferroelectricity in ABO3 crystals was expanded to show that, depending on the number of electrons in the dn shell of the transition metal ion B4+ and their low spin or high spin arrangement (which controls the symmetry and spin multiplicity of the ground and PJTE active excited states of the [BO6] center), the ferroelectricity may coexist with a magnetic moment (multiferroicity). Moreover, in combination with the temperature dependent spin crossover phenomenon (which changes the spin multiplicity), this kind of multiferroicity may lead to a novel effect known as a magnetic-ferroelectric crossover.[30]
Solid state magnetic-dielectric bistability. Similar to the above-mentioned molecular bistability induced by the hidden PJTE, a magnetic-dielectric bistability due to two coexisting equilibrium configurations with corresponding properties may take place also in crystals with transition metal centers, subject to the electronic configuration with half-filled e2 or t3 shells.[27] As in molecular systems, the latter produce a hidden PJTE and local bistability which, distinguished from the molecular case, are enhanced by the cooperative interactions, thus acquiring larger lifetimes. This crystal bistability was proved by calculations for LiCuO2 and NaCuO2 crystals, in which the Cu3+ ion has the electronic e2(d8) configuration (similar to the CuF3 molecule).[27]
Giant enhancement of observable properties in interaction with external perturbations. In a recent development it was shown that in inorganic crystals with PJTE centers, in which the local distortions are not ordered (before the phase transition to the cooperative phase), the effect of interaction with external perturbations contains an orientational contribution which enhances the observable properties by several orders of magnitude. This was demonstrated on the properties of crystals like paraelectric BaTiO3 in interaction with electric fields (in permittivity and electrostriction), or under a strain gradient (flexoelectricity). These giant enhancement effects occur due to the dynamic nature of the PJTE local dipolar distortions (their tunneling between the equivalent minima); the independently rotating dipole moments on each center become oriented (frozen) along the external perturbation resulting in an orientational polarization which is not there in the absence of the PJTE[31][32]
References
- ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 1.12 1.13 Bersuker, Isaac B. (9 January 2013). "Pseudo-Jahn–Teller Effect—A Two-State Paradigm in Formation, Deformation, and Transformation of Molecular Systems and Solids". Chemical Reviews (American Chemical Society (ACS)) 113 (3): 1351–1390. doi:10.1021/cr300279n. ISSN 0009-2665. PMID 23301718.
- ↑ 2.0 2.1 Öpik, U.; Pryce, M. H. L. (29 January 1957). "Studies of the Jahn-Teller effect. I. A survey of the static problem". Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences (The Royal Society) 238 (1215): 425–447. doi:10.1098/rspa.1957.0010. ISSN 2053-9169. Bibcode: 1957RSPSA.238..425O.
- ↑ Herzberg, G.; Teller, E. (1933). "Schwingungsstruktur der Elektronenübergänge bei mehratomigen Molekülen" (in de). Zeitschrift für Physikalische Chemie 21B (1): 410–446. doi:10.1515/zpch-1933-2136. ISSN 2196-7156.
- ↑ Murrell, J N; Pople, J A (1 February 1956). "The Intensities of the Symmetry-forbidden Electronic Bands of Benzene". Proceedings of the Physical Society. Section A (IOP Publishing) 69 (3): 245–252. doi:10.1088/0370-1298/69/3/307. ISSN 0370-1298. Bibcode: 1956PPSA...69..245M.
- ↑ Liehr, A. D. (1958). "Interaction of the vibrational and electronic motion in some simple conjugated hydrocarbons. I. Exact calculation of the intensity of the 1A1g → 1B1u, 1B2u, vibronic transitions of benzene". Zeitschrift für Naturforschung A 13 (6): 311. doi:10.1515/zna-1958-0601. http://zfn.mpdl.mpg.de/data/Reihe_A/13/ZNA-1958-13a-0311.pdf.
- ↑ Longuet-Higgins, H. C.; Salem, L. (26 May 1959). "The alternation of bond lengths in long conjugated chain molecules". Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences (The Royal Society) 251 (1265): 172–185. doi:10.1098/rspa.1959.0100. ISSN 2053-9169. Bibcode: 1959RSPSA.251..172L.
- ↑ Bader, R.F.W. (1960). "An interpretation of potential interaction constants in terms of low-lying excited states". Molecular Physics (Informa UK Limited) 3 (2): 137–151. doi:10.1080/00268976000100161. ISSN 0026-8976. Bibcode: 1960MolPh...3..137B.
- ↑ Fulton, Robert L.; Gouterman, Martin (1961). "Vibronic Coupling. I. Mathematical Treatment for Two Electronic States". The Journal of Chemical Physics (AIP Publishing) 35 (3): 1059–1071. doi:10.1063/1.1701181. ISSN 0021-9606. Bibcode: 1961JChPh..35.1059F.
- ↑ 9.0 9.1 9.2 Bersuker, I.B. (1966). "On the origin of ferroelectricity in perovskite-type crystals". Physics Letters (Elsevier BV) 20 (6): 589–590. doi:10.1016/0031-9163(66)91127-9. ISSN 0031-9163. Bibcode: 1966PhL....20..589B.
- ↑ 10.0 10.1 10.2 10.3 R. Englman "The Jahn–Teller Effect in Molecules and Crystals", Wiley-Interscience, (1972). ISBN:9780471241683
- ↑ 11.0 11.1 11.2 G. Pearson, "Symmetry Rules for Chemical Reactions. Orbital Topology for Elementary Processes", Wiley: New York, 1976.
- ↑ Borden, Weston Thatcher; Davidson, Ernest R.; Feller, David (1980). "Potential surfaces for (NH)32+ triaziridenyl dication". Journal of the American Chemical Society (American Chemical Society (ACS)) 102 (16): 5302–5311. doi:10.1021/ja00536a031. ISSN 0002-7863.
- ↑ Köuppel, H.; Domcke, W.; Cederbaum, L. S. (1 January 1984). "Multimode Molecular Dynamics Beyond the Born-Oppenheimer Approximation". Advances in Chemical Physics. Hoboken, NJ, USA: John Wiley & Sons, Inc.. pp. 59–246. doi:10.1002/9780470142813.ch2. ISBN 978-0-470-14281-3.
- ↑ Bersuker, Isaac B.; Gorinchoi, Natalia N.; Polinger, Victor Z. (1984). "On the origin of dynamic instability of molecular systems". Theoretica Chimica Acta (Springer Nature) 66 (3–4): 161–172. doi:10.1007/bf00549666. ISSN 0040-5744.
- ↑ 15.0 15.1 15.2 15.3 15.4 15.5 15.6 15.7 Bersuker, Isaac B.; Polinger, Victor Z. (1989). "Vibronic Interactions in Molecules and Crystals". Springer Series in Chemical Physics. 49. Berlin, Heidelberg: Springer Berlin Heidelberg. doi:10.1007/978-3-642-83479-0. ISBN 978-3-642-83481-3.
- ↑ 16.0 16.1 16.2 16.3 16.4 16.5 16.6 16.7 16.8 I. B. Bersuker, "The Jahn–Teller effect", Cambridge University Press, Cambridge UK, 2006.
- ↑ 17.0 17.1 17.2 Bersuker, Isaac B. (5 April 2016). "Spontaneous Symmetry Breaking in Matter Induced by Degeneracies and Pseudodegeneracies". Advances in Chemical Physics. 160. Hoboken, NJ: John Wiley & Sons, Inc. pp. 159–208. doi:10.1002/9781119165156.ch3. ISBN 978-1-119-16515-6.
- ↑ 18.0 18.1 J. K. Burdett, "Molecular Shapes. Theoretical Models of Inorganic Stereochemistry", Wiley: New York, 1980.
- ↑ 19.0 19.1 R. Hoffmann, "Solids and Surfaces: A Chemist's View of Bonding in Extended Structures", VCH: New York, 1988.
- ↑ R. E. Peierls "Quantum theory of solids", Oxford, Clarendon, 1955.
- ↑ Hermoso, Willian; Liu, Yang; Bersuker, Isaac B. (17 September 2014). "Novel Effect Induced by Pseudo-Jahn–Teller Interactions: Broken Cylindrical Symmetry in Linear Molecules". Journal of Chemical Theory and Computation (American Chemical Society (ACS)) 10 (10): 4377–4388. doi:10.1021/ct500626j. ISSN 1549-9618. PMID 26588135.
- ↑ Ilkhani, Ali R.; Gorinchoy, Natalia N.; Bersuker, Isaac B. (October 2015). "Pseudo Jahn–Teller effect in distortion and restoration of planar configurations of tetra-heterocyclic 1,2-diazetes C2N2E4, E=H, F, Cl, Br". Chemical Physics 460: 106–110. doi:10.1016/j.chemphys.2015.07.015. Bibcode: 2015CP....460..106I.
- ↑ Pokhodnya, Konstantin; Olson, Christopher; Dai, Xuliang; Schulz, Douglas L.; Boudjouk, Philip; Sergeeva, Alina P.; Boldyrev, Alexander I. (7 January 2011). "Flattening a puckered cyclohexasilane ring by suppression of the pseudo-Jahn–Teller effect". The Journal of Chemical Physics 134 (1): 014105. doi:10.1063/1.3516179. PMID 21218995. Bibcode: 2011JChPh.134a4105P.
- ↑ Ivanov, Alexander S.; Bozhenko, Konstantin V.; Boldyrev, Alexander I. (30 July 2012). "On the Suppression Mechanism of the Pseudo-Jahn–Teller Effect in Middle E (E = P, As, Sb) Rings of Triple-Decker Sandwich Complexes". Inorganic Chemistry 51 (16): 8868–8872. doi:10.1021/ic300786w. PMID 22845625.
- ↑ Ilkhani, Ali Reza (October 2015). "Pseudo Jahn-Teller origin of puckering in cyclohexahomoatomic molecules E6 (E = S, Se, Te) and restoring S6 planar ring configuration". Journal of Molecular Structure 1098: 21–25. doi:10.1016/j.molstruc.2015.05.029. Bibcode: 2015JMoSt1098...21I.
- ↑ Pratik, Saied Md; Datta, Ayan (25 June 2015). "1,4-Dithiine—Puckered in the Gas Phase but Planar in Crystals: Role of Cooperativity". The Journal of Physical Chemistry C 119 (27): 15770–15776. doi:10.1021/acs.jpcc.5b04908.
- ↑ 27.0 27.1 27.2 Garcia-Fernandez, Pablo; Bersuker, Isaac B. (17 June 2011). "Class of Molecular and Solid State Systems with Correlated Magnetic and Dielectric Bistabilities Induced by the Pseudo Jahn-Teller Effect". Physical Review Letters (American Physical Society (APS)) 106 (24): 246406. doi:10.1103/physrevlett.106.246406. ISSN 0031-9007. PMID 21770587. Bibcode: 2011PhRvL.106x6406G.
- ↑ Bersuker, I B (19 May 2017). "The Jahn-Teller and pseudo Jahn-Teller effect in materials science". Journal of Physics: Conference Series (IOP Publishing) 833 (1): 012001. doi:10.1088/1742-6596/833/1/012001. ISSN 1742-6588. Bibcode: 2017JPhCS.833a2001B.
- ↑ Ilkhani, Ali Reza; Wang, Zhibo (3 January 2019). "Instability in pyramidal–tetrahedral structure including elements from group 14 induced by pseudo-Jahn–Teller effect". Theoretical Chemistry Accounts 138 (1): 14. doi:10.1007/s00214-018-2402-1.
- ↑ Bersuker, Isaac B. (28 March 2012). "Pseudo Jahn-Teller Origin of Perovskite Multiferroics, Magnetic-Ferroelectric Crossover, and Magnetoelectric Effects: Thed0−d10 Problem". Physical Review Letters (American Physical Society (APS)) 108 (13): 137202. doi:10.1103/physrevlett.108.137202. ISSN 0031-9007. PMID 22540723. Bibcode: 2012PhRvL.108m7202B.
- ↑ Bersuker, Isaac B. (16 November 2015). "Giant permittivity and electrostriction induced by dynamic Jahn-Teller and pseudo Jahn-Teller effects". Applied Physics Letters (AIP Publishing) 107 (20): 202904. doi:10.1063/1.4936190. ISSN 0003-6951. Bibcode: 2015ApPhL.107t2904B.
- ↑ Bersuker, I. B. (12 January 2015). "Pseudo Jahn–Teller effect in the origin of enhanced flexoelectricity". Applied Physics Letters (AIP Publishing) 106 (2): 022903. doi:10.1063/1.4905679. ISSN 0003-6951. Bibcode: 2015ApPhL.106b2903B.
 |


