Physics:Jahn–Teller effect
The Jahn–Teller effect (JT effect or JTE) is an important mechanism of spontaneous symmetry breaking in molecular and solid-state systems which has far-reaching consequences in different fields, and is responsible for a variety of phenomena in spectroscopy, stereochemistry, crystal chemistry, molecular and solid-state physics, and materials science. The effect is named for Hermann Arthur Jahn and Edward Teller, who first reported studies about it in 1937.[1]:sec. 13.4
Simplified overview
The Jahn–Teller effect, sometimes also referred to as Jahn–Teller distortion, describes the geometrical distortion of molecules and ions that results from certain electron configurations. The Jahn–Teller theorem essentially states that any non-linear molecule with a spatially degenerate electronic ground state will undergo a geometrical distortion that removes that degeneracy, because the distortion lowers the overall energy of the species. For a description of another type of geometrical distortion that occurs in crystals with substitutional impurities see article off-center ions.
Transition metal chemistry


The Jahn–Teller effect is most often encountered in octahedral complexes of the transition metals.[3] The phenomenon is very common in six-coordinate copper(II) complexes.[4] The d9 electronic configuration of this ion gives three electrons in the two degenerate eg orbitals, leading to a doubly degenerate electronic ground state. Such complexes distort along one of the molecular fourfold axes (always labelled the z axis), which has the effect of removing the orbital and electronic degeneracies and lowering the overall energy. The distortion normally takes the form of elongating the bonds to the ligands lying along the z axis, but occasionally occurs as a shortening of these bonds instead (the Jahn–Teller theorem does not predict the direction of the distortion, only the presence of an unstable geometry). When such an elongation occurs, the effect is to lower the electrostatic repulsion between the electron-pair on the Lewis basic ligand and any electrons in orbitals with a z component, thus lowering the energy of the complex. The inversion centre is preserved after the distortion.
In octahedral complexes, the Jahn–Teller effect is most pronounced when an odd number of electrons occupy the eg orbitals. This situation arises in complexes with the configurations d9, low-spin d7 or high-spin d4 complexes, all of which have doubly degenerate ground states. In such compounds the eg orbitals involved in the degeneracy point directly at the ligands, so distortion can result in a large energetic stabilisation. Strictly speaking, the effect also occurs when there is a degeneracy due to the electrons in the t2g orbitals (i.e. configurations such as d1 or d2, both of which are triply degenerate). In such cases, however, the effect is much less noticeable, because there is a much smaller lowering of repulsion on taking ligands further away from the t2g orbitals, which do not point directly at the ligands (see the table below). The same is true in tetrahedral complexes (e.g. manganate: distortion is very subtle because there is less stabilisation to be gained because the ligands are not pointing directly at the orbitals.
The expected effects for octahedral coordination are given in the following table:
| Number of d electrons | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| High/Low Spin | HS | LS | HS | LS | HS | LS | HS | LS | ||||||
| Strength of J–T Effect | w | w | s | w | w | w | w | s | s | |||||
w: weak Jahn–Teller effect (t2g orbitals unevenly occupied)
s: strong Jahn–Teller effect expected (eg orbitals unevenly occupied)
blank: no Jahn–Teller effect expected.
The Jahn–Teller effect is manifested in the UV-VIS absorbance spectra of some compounds, where it often causes splitting of bands. It is readily apparent in the structures of many copper(II) complexes.[5] Additional, detailed information about the anisotropy of such complexes and the nature of the ligand binding can be however obtained from the fine structure of the low-temperature electron spin resonance spectra.

Related effects
The underlying cause of the Jahn–Teller effect is the presence of molecular orbitals that are both degenerate and open shell (i.e., incompletely occupied). This situation is not unique to coordination complexes and can be encountered in other areas of chemistry. In organic chemistry the phenomenon of antiaromaticity has the same cause and also often sees molecules distorting; as in the case of cyclobutadiene[6] and cyclooctatetraene (COT).[7]
Advanced treatment
The Jahn–Teller theorem
The JT theorem can be stated in different forms, two of which are given here:
- "A nonlinear polyatomic system in a spatially degenerate electronic state distorts spontaneously in such a way that the degeneracy is lifted and a new equilibrium structure of lower symmetry is attained."
Alternatively and considerably shorter:
- "... stability and degeneracy are not possible simultaneously unless the molecule is a linear one ...".[8]
Spin-degeneracy was an exception in the original treatment and was later treated separately.[9]
The formal mathematical proof of the Jahn–Teller theorem rests heavily on symmetry arguments, more specifically the theory of molecular point groups. The argument of Jahn and Teller assumes no details about the electronic structure of the system. Jahn and Teller made no statement about the strength of the effect, which may be so small that it is immeasurable. Indeed, for electrons in non-bonding or weakly bonding molecular orbitals, the effect is expected to be weak. However, in many situations the JT effect is important.
Historic developments
Interest in the JTE increased after its first experimental verification. Various model systems were developed probing the degree of degeneracy and the type of symmetry.[10] These were solved partly analytically and partly numerically to obtain the shape of the pertinent potential energy surfaces (PES) and the energy levels for the nuclear motion on the JT-split PES. These energy levels are not vibrational energy levels in the traditional sense because of the intricate coupling to the electronic motion that occurs, and are better termed vibronic energy levels. The new field of ‘vibronic coupling’ or ‘vibronic coupling theory’ was born.
A further breakthrough occurred upon the advent of modern ("ab initio") electronic structure calculations whereby the relevant parameters characterising JT systems can be reliably determined from first principles. Thus one could go beyond studies of model systems that explore the effect of parameter variations on the PES and vibronic energy levels; one could also go on beyond fitting these parameters to experimental data without clear knowledge about the significance of the fit. Instead, well-founded theoretical investigations became possible which greatly improved the insight into the phenomena at hand and into the details of the underlying mechanisms.

While recognizing the JTE distortion as a concrete example of the general spontaneous symmetry breaking mechanism, the exact degeneracy of the involved electronic state was identified as a non-essential ingredient for this symmetry breaking in polyatomic systems. Even systems that in the undistorted symmetric configuration present electronic states which are near in energy but not precisely degenerate, can show a similar tendency to distort. The distortions of these systems can be treated within the related theory of the pseudo Jahn–Teller effect (in the literature often referred to as "second-order JTE"). This mechanism is associated to the vibronic couplings between adiabatic PES separated by nonzero energy gaps across the configuration space: its inclusion extends the applicability of JT-related models to symmetry breaking in a far broader range of molecular and solid-state systems.
Chronology:
- 1934: Lev Landau, in discussion with Edward Teller, suggested that electronic states of certain degenerate nuclear configurations are unstable with respect to nuclear displacements that lower the symmetry (see 'An historical note' by Englman[11]).
- 1937: Hermann Arthur Jahn and Edward Teller formulated what is now known as the Jahn–Teller theorem.[8]
- 1939: John Hasbrouck Van Vleck extended the Jahn–Teller theorem to ions in crystals. As attempts to observe the Jahn–Teller effect experimentally had been unconvincing, he noted that 'it is of great merit of the Jahn–Teller effect that it disappears when not needed'.[12][13]
- 1950–2: Brebis Bleaney and co-workers first obtained unambiguous experimental evidence of the Jahn–Teller effect, by carrying out electron paramagnetic resonance studies on paramagnetic ions in crystals[14][15]
- 1957–8: Öpik and Pryce showed that spin–orbit coupling can stabilise symmetric configurations against distortions from a weak JTE.[16] Moffitt et al.[17][18] and Longuet-Higgins et al.[19] argued that the states of JT systems have inextricably mixed electronic and vibrational components, which they called vibronic states, with energies very different to the electronic states.
- 1962–4: Isaac Bersuker[20] and Mary O’Brien [21] investigated tunnelling in the lowest-energy vibronic states, the so-called tunnelling splitting, and the dynamic nature of the JT effect. The article by O'Brien shows the influence of the geometric phase factor (later called Berry phase) on the ordering of the vibronic states.
- 1965: Frank Ham realised the effect of coherent dynamics on the measurement of observables. This influence can be described in terms of reduction factors multiplying orbital operators[22] and specific formulae were proposed for the magnetism of JT ions.
- 1984: Generalization of the concept of geometric phase by Berry[23] (or Berry phase as it is also known) provided a general background to aid understanding of the rotation-dependent phase associated with the electronic and vibrational wavefunction of JT systems, as discovered by Longuet-Higgins,[19] and further discussed by Herzberg and Longuet-Higgins,[24] Longuet-Higgins,[25] O'Brien,[21] and Mead and Truhlar.[26]
- 1990s: Advances in computing power meant that ab initio methods including those based on the Density Functional Theory started to be used to solve JT problems.
Relation to important discoveries
- In 1985, Harry Kroto and co-workers discovered a class of closed-cage carbon molecules known as fullerenes.[27] Buckminsterfullerene (C60), which has icosahedral symmetry, becomes JT-active upon addition or removal of one electron.[28] The ordering of energy levels may not be the same as that predicted by Hund's rule.
- Discovery in 1986 by Bednorz and Müller of superconductivity in cuprates with a transition temperature of 35 K,[29] which was higher than the upper limit allowed according to standard BCS theory, was motivated by earlier work by Müller on JT ions in crystals.
- Colossal magnetoresistance, a property of manganese-based perovskites and other materials, has been explained in terms of competition between dynamic Jahn–Teller and double-exchange effects.[30]
- Peierls theorem, which states that a one-dimensional equally spaced chain of ions with one electron per ion is unstable, has common roots with the JT effect.
Theory
Symmetry of JT systems and categorisation using group theory
A given JT problem will have a particular point group symmetry, such as Td symmetry for magnetic impurity ions in semiconductors or Ih symmetry for the fullerene C60. JT problems are conventionally classified using labels for the irreducible representations (irreps) that apply to the symmetry of the electronic and vibrational states. For example, E ⊗ e would refer to an electronic doublet state transforming as E coupled to a vibrational doublet state transforming as e.
In general, a vibrational mode transforming as Λ will couple to an electronic state transforming as Γ if the symmetric part of the Kronecker product [Γ ⊗ Γ]S contains Λ, unless Γ is a double group representation when the antisymmetric part {Γ ⊗ Γ}A is considered instead. Modes which do couple are said to be JT-active.
As an example, consider a doublet electronic state E in cubic symmetry. The symmetric part of E ⊗ E is A1 + E. Therefore, the state E will couple to vibrational modes transforming as a1 and e. However, the a1 modes will result in the same energy shift to all states and therefore do not contribute to any JT splitting. They can therefore be neglected. The result is an E ⊗ e JT effect. This JT effect is experienced by triangular molecules X3, tetrahedral molecules ML4, and octahedral molecules ML6 when their electronic state has E symmetry.
Components of a given vibrational mode are also labelled according to their transformation properties. For example, the two components of an e mode are usually labelled and , which in octahedral symmetry transform as and respectively.
The JT Hamiltonian
Eigenvalues of the Hamiltonian of a polyatomic system define PESs as functions of normal modes of the system (i.e. linear combinations of the nuclear displacements with specific symmetry properties). At the reference point of high symmetry, where the symmetry-induced degeneracy occurs, several of the eigenvalues coincide. By a detailed and laborious analysis, Jahn and Teller showed that – excepting linear molecules – there are always first-order terms in an expansion of the matrix elements of the Hamiltonian in terms of symmetry-lowering (in the language of group theory: non-totally symmetric) normal modes. These linear terms represent forces that distort the system along these coordinates and lift the degeneracy. The point of degeneracy can thus not be stationary, and the system distorts toward a stationary point of lower symmetry where stability can be attained.
Proof of the JT theorem follows from the theory of molecular symmetry (point group theory). A less rigorous but more intuitive explanation is given in section .
To arrive at a quantitative description of the JT effect, the forces appearing between the component wave functions are described by expanding the Hamiltonian in a power series in the . Owing to the very nature of the degeneracy, the Hamiltonian takes the form of a matrix referring to the degenerate wave function components. A matrix element between states and generally reads as:
The expansion can be truncated after terms linear in the , or extended to include terms quadratic (or higher) in the .
The adiabatic potential energy surfaces (APES) are then obtained as the eigenvalues of this matrix. In the original paper it is proven that there are always linear terms in the expansion. It follows that the degeneracy of the wave function cannot correspond to a stable structure.
Potential energy surfaces
Mexican-hat potential
In mathematical terms, the APESs characterising the JT distortion arise as the eigenvalues of the potential energy matrix. Generally, the APESs take the characteristic appearance of a double cone, circular or elliptic, where the point of contact, i.e. degeneracy, denotes the high-symmetry configuration for which the JT theorem applies. For the above case of the linear E ⊗ e JT effect the situation is illustrated by the APES
displayed in the figure, with part cut away to reveal its shape, which is known as a Mexican Hat potential. Here,
is the frequency of the vibrational e mode,
is its mass and
is a measure of the strength of the JT coupling.

The conical shape near the degeneracy at the origin makes it immediately clear that this point cannot be stationary, that is, the system is unstable against asymmetric distortions, which leads to a symmetry lowering. In this particular case there are infinitely many isoenergetic JT distortions. The giving these distortions are arranged in a circle, as shown by the red curve in the figure. Quadratic coupling or cubic elastic terms lead to a warping along this "minimum energy path", replacing this infinite manifold by three equivalent potential minima and three equivalent saddle points. In other JT systems, linear coupling results in discrete minima.
Conical intersections
The high symmetry of the double-cone topology of the linear E ⊗ e JT system directly reflects the high underlying symmetry. It is one of the earliest (if not the earliest) examples in the literature of a conical intersection of potential energy surfaces. Conical intersections have received wide attention in the literature starting in the 1990s and are now considered paradigms of nonadiabatic excited-state dynamics, with far-reaching consequences in molecular spectroscopy, photochemistry and photophysics. Some of these will be commented upon further below. In general, conical intersections are far less symmetric than depicted in the figure. They can be tilted and elliptical in shape etc., and also peaked and sloped intersections have been distinguished in the literature. Furthermore, for more than two degrees of freedom, they are not point-like structures but instead they are seams and complicated, curved hypersurfaces, also known as intersection space. The coordinate sub-space displayed in the figure is also known as a branching plane.
Implications for dynamics
The characteristic shape of the JT-split APES has specific consequences for the nuclear dynamics, here considered in the fully quantum sense. For sufficiently strong JT coupling, the minimum points are sufficiently far (at least by a few vibrational energy quanta) below the JT intersection. Two different energy regimes are then to be distinguished, those of low and high energy.
- In the low-energy regime the nuclear motion is confined to regions near the "minimum energy points". The distorted configurations sampled impart their geometrical parameters on, for example, the rotational fine structure in a spectrum. Due to the existence of barriers between the various minima in the APES, like those appearing due to the warping of the , motion on the low-energy regime is usually classified as either a static JTE, dynamic JTE or incoherent hopping. Each regime shows particular fingerprints on experimental measurements.
- Static JTE: In this case, the system is trapped in one of the lowest-energy minima of the APES (usually determined by small perturbations created by the environment of the JT system) and does not have enough energy to cross the barrier towards another minimum during the typical time associated to the measurement. Quantum dynamical effects like tunnelling are negligible, and effectively the molecule or solid displays the low symmetry associated with a single minimum.
- Dynamic JTE:[31] In this case, the barriers are sufficiently small compared to, for example, the zero-point energy associated to the minima, so that vibronic wavefunctions (and all observables) display the symmetry of the reference (undistorted) system. In the linear E ⊗ e problem, the motion associated to this regime would be around the circular path in the figure. When the barrier is sufficiently small, this is called (free) pseudorotation (not to be confused with the rotation of a rigid body in space, see difference between real and pseudo rotations illustrated here for the fullerene molecule C60). When the barrier between the minima and the saddle points on the warped path exceeds a vibrational quantum, pseudorotational motion is slowed down and occurs through tunnelling. This is called hindered pseudorotation. In both free and hindered pseudorotation, the important phenomenon of the geometric (Berry) phase alters the ordering of the levels.
- Incoherent hopping: Another way in which the system can overcome the barrier is through thermal energy. In this case, while the system moves throughout the minima of the system, the state is not a quantum coherent one but a statistical mixture. This difference can be observed experimentally.
- The dynamics is quite different for high energies, such as occur from an optical transition from a non-degenerate initial state with a high-symmetry (JT undistorted) equilibrium geometry into a JT distorted state. This leads the system to the region near the conical intersection of the JT-split APES in the centre of the figure. Here the nonadiabatic couplings become very large and the behaviour of the system cannot be described within the familiar Born–Oppenheimer (BO) separation between the electronic and nuclear motions. The nuclear motion ceases to be confined to a single, well-defined APES and the transitions between the adiabatic surfaces occur yielding effects like Slonzcewsky resonances. In molecules this is usually a femtosecond timescale, which amounts to ultrafast (femtosecond) internal conversion processes, accompanied by broad spectral bands also under isolated-molecule conditions and highly complex spectral features. Examples for these phenomena will be covered in section .
As already stated above, the distinction of low and high energy regimes is valid only for sufficiently strong JT couplings, that is, when several or many vibrational energy quanta fit into the energy window between the conical intersection and the minimum of the lower JT-split APES. For the many cases of small to intermediate JT couplings this energy window and the corresponding adiabatic low-energy regime does not exist. Rather, the levels on both JT-split APES are intricately mixed for all energies and the nuclear motion always proceeds on both JT split APES simultaneously.
Ham factors
In 1965, Frank Ham [22] proposed that the dynamic JTE could reduce the expected values of observables associated with the orbital wavefunctions due to the superposition of several electronic states in the total vibronic wavefunction. This effect leads, for example, to a partial quenching of the spin–orbit interaction[22][32] and allowed the results of previous Electron Paramagnetic Resonance (EPR) experiments to be explained.
In general, the result of an orbital operator acting on vibronic states can be replaced by an effective orbital operator acting on purely electronic states. In first order, the effective orbital operator equals the actual orbital operator multiplied by a constant, whose value is less than one, known as a first-order (Ham) reduction factor. For example, within a triplet T1 electronic state, the spin–orbit coupling operator can be replaced by , where is a function of the strength of the JT coupling which varies from 1 in zero coupling to 0 in very strong coupling. Furthermore, when second-order perturbation corrections are included, additional terms are introduced involving additional numerical factors, known as second-order (Ham) reduction factors. These factors are zero when there is no JT coupling but can dominate over first-order terms in strong coupling, when the first-order effects have been significantly reduced.[10]
Reduction factors are particularly useful for describing experimental results, such as EPR and optical spectra, of paramagnetic impurities in semiconducting, dielectric, diamagnetic and ferrimagnetic hosts.
Modern developments
For a long time, applications of JT theory consisted mainly in parameter studies (model studies) where the APES and dynamical properties of JT systems have been investigated as functions on the system parameters such as coupling constants etc. Fits of these parameters to experimental data were often doubtful and inconclusive. The situation changed in the 1980s when efficient ab initio methods were developed and computational resources became powerful enough to allow for a reliable determination of these parameters from first principles.[33] Apart from wave function-based techniques (which are sometimes considered genuinely ab initio in the literature) the advent of density functional theory (DFT) opened up new avenues to treat larger systems including solids. This allowed details of JT systems to be characterised and experimental findings to be reliably interpreted. It lies at the heart of most developments addressed in section .
Two different strategies are conceivable and have been used in the literature. One can
- take the applicability of a certain coupling scheme for granted and limit oneself to determine the parameters of the model, for example from the energy gain achieved through the JT distortion, also termed JT stabilisation energy.
- map parts of the APES in whole or reduced dimensionality and thus get an insight into the applicability of the model, possibly also deriving ideas how to extend it.
Naturally, the more accurate approach (2) may be limited to smaller systems, while the simpler approach (1) lends itself to studies of larger systems.
Applications
Effects on structure
Small molecules and ions
The JT distortion of small molecules (or molecular ions) is directly deduced from electronic structure calculations of their APES (through DFT and/or ab initio computations). These molecules / ions are often radicals, such as trimers of alkali atoms (Li3 and Na3), that have unpaired spins and in particular in (but not restricted to) doublet states. Besides the JTE in 2E′ and 2E″ states, also the pseudo JTE between an E state and a nearby A state may play a role. The JT distortion reduces the symmetry from D3h to C2v (see figure), and it depends on the details of the interactions whether the isosceles triangle has an acute or an obtuse-angled (such as Na3) minimum energy structure. Natural extensions are systems like NO3 and NH3+ where a JT distortion has been documented in the literature for ground or excited electronic states.

A somewhat special role is played by tetrahedral systems like CH4+ and P4+. Here threefold degenerate electronic states and vibrational modes come into play. Nevertheless, also twofold degeneracies continue to be important. The dynamics of Jahn-Teller distortion in CH4+ has been characterized by transient X-ray absorption spectroscopy, revealing that symmetry breaking occurs within ten femtoseconds in this prototypical system.[34]
Among larger systems, a focus in the literature has been on benzene and its radical cation, as well as on their halo (especially fluoro) derivatives. Already in the early 1980s, a wealth of information emerged from the detailed analysis of experimental emission spectra of 1,3,5- trifluoro- and hexafluoro (and chloro) benzene radical cations. The Jahn–Teller effect in the 1,3,5-trifluoro benzene radical cation is discussed in Section 13.4.2 of the textbook by Bunker and Jensen.[1] For the parent benzene cation one has to rely on photoelectron spectra with comparatively lower resolution because this species does not fluoresce (see also section ). Rather detailed ab initio calculations have been carried out which document the JT stabilization energies for the various (four) JT active modes and also quantify the moderate barriers for the JT pseudorotation.
Finally, a somewhat special role is played by systems with a fivefold symmetry axis like the cyclopentadienyl radical. Careful laser spectroscopic investigations have shed useful light on the JT interactions. In particular they reveal that the barrier to pseudorotation almost vanishes (the system is highly "fluxional") which can be attributed to the fact that the 2nd-order coupling terms vanish by symmetry and the leading higher-order terms are of 4th order.
Coordination chemistry
The JTE is usually stronger where the electron density associated with the degenerate orbitals is more concentrated. This effect therefore plays a large role in determining the structure of transition metal complexes with active internal 3d orbitals.

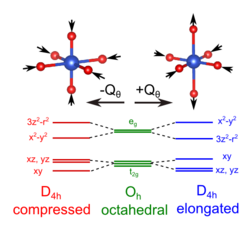
The most iconic and prominent of the JT systems in coordination chemistry is probably the case of Cu(II) octahedral complexes. While in perfectly equivalent coordination, like a CuF6 complex associated to a Cu(II) impurity in a cubic crystal like KMgF3, perfect octahedral (Oh) symmetry is expected. In fact a lower tetragonal symmetry is usually found experimentally. The origin of this JTE distortion it revealed by examining the electronic configuration of the undistorted complex. For an octahedral geometry, the five 3d orbitals partition into t2g and eg orbitals (see diagram). These orbitals are occupied by nine electrons corresponding to the electronic configuration of Cu(II). Thus, the t2g shell is filled, and the eg shell contains 3 electrons. Overall the unpaired electron produces a 2Eg state, which is Jahn–Teller active. The third electron can occupy either of the orbitals comprising the eg shell: the mainly orbital or the mainly orbital. If the electron occupies the mainly level, which antibonding orbital the final geometry of the complex would be elongated as the axial ligands will be pushed away to reduce the global energy of the system. On the other hand, if the electron went into the mainly antibonding orbital the complex would distort into a compressed geometry. Experimentally elongated geometries are overwhelmingly observed and this fact has been attributed both to metal-ligand anharmonic interactions [16] and 3d-4s hybridisations.[35] Given that all the directions containing a fourfold axis are equivalent the distortion is equally likely to happen in any of these orientations. From the electronic point of view this means that the and orbitals, that are degenerate and free to hybridise in the octahedral geometry, will mix to produce appropriate equivalent orbitals in each direction like or .
The JTE is not just restricted to Cu(II) octahedral complexes. There are many other configurations, involving changes both in the initial structure and electronic configuration of the metal that yield degenerate states and, thus, JTE. However, the amount of distortion and stabilisation energy of the effect is strongly dependent on the particular case. In octahedral Cu(II), the JTE is particularly strong because
- the degenerate orbitals display a strongly antibonding σ character
- Cu is a transition metal with a relatively strong electronegativity yielding more covalent bonds than other metals which allows to increase the JT linear coupling constant.
In other configurations involving π or δ bonding, like for example when the degenerate state is associated to the t2g orbitals of an octahedral configuration, the distortion and stabilisation energies are usually much smaller and the possibility of not observing the distortion due to dynamic JT effects is much higher. Similarly for rare-earth ions where covalency is very small, the distortions associated to the JTE are usually very weak.
Importantly, the JTE is associated with strict degeneracy in the electronic subsystem and so it cannot appear in systems without this property. For example, the JTE is often associated to cases like quasi-octahedral CuX2Y4 complexes where the distances to X and Y ligands are clearly different. However, the intrinsic symmetry of these complexes is already tetragonal and no degenerate eg orbital exists, having split into a1g (mainly ) and b1g (mainly ) orbitals due to the different electronic interactions with axial X ligands and equatorial Y ligands. In this and other similar cases some remaining vibronic effects related to the JTE are still present but are quenched with respect to the case with degeneracy due to the splitting of the orbitals.
Spectroscopy and reactivity
From spectra with rotational resolution, moments of inertia and hence bond lengths and angles can be determined "directly" (at least in principle). From less well-resolved spectra one can still determine important quantities like JT stabilization energies and energy barriers (e.g. to pseudorotation). However, in the whole spectral intensity distribution of an electronic transition more information is encoded. It has been used to decide on the presence (or absence) of the geometric phase which is accumulated during the pseudorotational motion around the JT (or other type of) conical intersection. Prominent examples of either type are the ground (X) or an excited (B) state of Na3. The Fourier transform of , the so-called autocorrelation function reflects the motion of the wavepacket after an optical (= vertical) transition to the APES of the final electronic state. Typically it will move on the timescale of a vibrational period which is (for small molecules) of the order of 5–50 fs, i.e. ultrafast. Besides a nearly periodic motion, mode–mode interactions with very irregular (also chaotic) behaviour and spreading of the wavepacket may also occur. Near a conical intersection this will be accompanied/complemented by nonradiative transitions (termed internal conversion) to other APESs occurring on the same ultrafast time scale.
For the JT case the situation is somewhat special, as compared to a general conical intersection, because the different JT potential sheets are symmetry-related to each other and have (exactly or nearly) the same energy minimum. The "transition" between them is thus more oscillatory than one would normally expect, and their time-averaged populations are close to 1/2. For a more typical scenario a more general conical intersection is "required".
The JT effect still comes into play, namely in combination with a different nearby, in general non-degenerate electronic state. The result is a pseudo Jahn–Teller effect, for example, of an E state interacting with an A state. This situation is common in JT systems, just as interactions between two nondegenerate electronic states are common for non-JT systems. Examples are excited electronic states of NH3+ and the benzene radical cation. Here, crossings between the E and A state APESs amount to triple intersections, which are associated with very complex spectral features (dense line structures and diffuse spectral envelopes under low resolution). The population transfer between the states is also ultrafast, so fast that fluorescence (proceeding on a nanosecond time scale) cannot compete. This helps to understand why the benzene cation, like many other organic radical cation, does not fluoresce.
To be sure, photochemical reactivity emerges when the internal conversion makes the system explore the nuclear configuration space such that new chemical species are formed. There is a plethora of femtosecond pump-probe spectroscopic techniques to reveal details of these processes occurring, for example, in the process of vision.
Solid-state problems
As proposed originally by Landau[36] free electrons in a solid, introduced for example by doping or irradiation, can interact with the vibrations of the lattice to form a localized quasi-particle known as a polaron. Strongly localized polarons (also called Holstein polarons) can condensate around high-symmetry sites of the lattice with electrons or holes occupying local degenerate orbitals that experience the JTE. These Jahn–Teller polarons break both translational and point group symmetries of the lattice where they are found and have been attributed important roles in effects like colossal magnetoresistance and superconductivity.
Paramagnetic impurities in semiconducting, dielectric, diamagnetic and ferrimagnetic hosts can all be described using a JT model. For example, these models were used extensively in the 1980s and 1990s to describe ions of Cr, V and Ti substituting for Ga in GaAs and GaP.
The fullerene C60 can form solid compounds with alkali metals known as fullerides. Cs3C60 can be superconducting at temperatures up to 38K under applied pressure,[37] whereas compounds of the form A4C60 are insulating (as reviewed by Gunnarsson[38]). JT effects both within the C60 molecules (intramolecular) and between C60 molecules (intermolecular) play a part in the mechanisms behind various observed properties in these systems. For example, they could mean that the Migdal–Eliashberg treatment of superconductivity breaks down. Also, the fullerides can form a so-called new state of matter known as a Jahn–Teller metal, where localised electrons coexist with metallicity and JT distortions on the C60 molecules persist.[39]
Cooperative JT effect in crystals
The JTE is usually associated with degeneracies that are well localised in space, like those occurring in a small molecule or associated to an isolated transition metal complex. However, in many periodic high-symmetry solid-state systems, like perovskites, some crystalline sites allow for electronic degeneracy giving rise under adequate compositions to lattices of JT-active centers. This can produce a cooperative JTE, where global distortions of the crystal occur due to local degeneracies.
In order to determine the final electronic and geometric structure of a cooperative JT system, it is necessary to take into account both the local distortions and the interaction between the different sites, which will take such form necessary to minimise the global energy of the crystal.
While works on the cooperative JTE started in the late fifties,[40][41] it was in 1960 that Kanamori[42] published the first work on the cooperative JTE where many important elements present in the modern theory for this effect were introduced. This included the use of pseudospin notation to discuss orbital ordering, and discussions of the importance of the JTE to discuss magnetism, the competition of this effect with the spin–orbit coupling and the coupling of the distortions with the strain of the lattice. This point was later stressed in the review by Gehring and Gehring[43] as being the key element to establish long-range order between the distortions in the lattice. An important part of the modern theory of the cooperative JTE,[44] can lead to structural phase transitions.
It is important to note that many cooperative JT systems would be expected to be metals from band theory as, to produce them, a degenerate orbital has to be partially filled and the associated band would be metallic. However, under the perturbation of the symmetry-breaking distortion associated to the cooperative JTE, the degeneracies in the electronic structure are destroyed and the ground state of these systems is often found to be insulating (see e.g.[45]). In many important cases like the parent compound for colossal magnetoresistance perovskites, LaMnO3, an increase of temperature leads to disorder in the distortions which lowers the band splitting due to the cooperative JTE, thus triggering a metal–insulator transition.
JT-related effects: Orbital ordering
In modern solid-state physics, it is common to classify systems according to the kind of degrees of freedom they have available, like electron (metals) or spin (magnetism). In crystals that can display the JTE, and before this effect is realised by symmetry-breaking distortions, it is found that there exists an orbital degree of freedom consisting of how electrons occupy the local degenerate orbitals. As initially discussed by Kugel and Khomskii,[46] not all configurations are equivalent. The key is the relative orientation of these occupied orbital, in the same way that spin orientation is important in magnetic systems, and the ground state can only be realised for some particular orbital pattern. Both this pattern and the effect giving rise to this phenomenon is usually denominated orbital-ordering.
In order to predict the orbital-ordering pattern, Kugel and Khomskii used a particularisation of the Hubbard model. In particular they established how superexchange interactions, usually described by the Anderson–Kanamori–Goodenough rules, change in the presence of degenerate orbitals. Their model, using a pseudospin representation for the local orbitals, leads to a Heisenberg-like model in which the ground state is a combination of orbital and spin patterns. Using this model it can be shown, for example, that the origin of the unusual ground insulating ferromagnetic state of a solid like K2CuF4 can be traced to its orbital ordering.
Even when starting from a relatively high-symmetry structure the combined effect of exchange interactions, spin–orbit coupling, orbital-ordering and crystal deformations activated by the JTE can lead to very low symmetry magnetic patterns with specific properties. For example, in CsCuCl3 an incommensurable helicoidal pattern appears both for the orbitals and the distortions along the -axis. Moreover, many of these compounds show complex phase diagrams when varying temperature or pressure.
References
- ↑ 1.0 1.1 Bunker, Philip R.; Jensen, Per (1998) Molecular Symmetry and Spectroscopy (2nd ed.). NRC Research Press, Ottawa [1]ISBN:9780660196282
- ↑ Persson, Ingmar (2010). "Hydrated metal ions in aqueous solution: How regular are their structures?". Pure and Applied Chemistry 82 (10): 1901–1917. doi:10.1351/PAC-CON-09-10-22.
- ↑ Shriver, D. F.; Atkins, P. W. (1999). Inorganic Chemistry (3rd ed.). Oxford University Press. pp. 235–236. ISBN 978-0-19-850330-9.
- ↑ Janes, Rob; Moore, Elaine A. (2004). Metal-ligand bonding. Royal Society of Chemistry. ISBN 978-0-85404-979-0. https://books.google.com/books?id=qsP7mmhqvj4C&dq=%22Jahn-Teller+distortion%22&pg=PA23.
- ↑ Frank, Patrick; Benfatto, Maurizio; Szilagyi, Robert K.; D'Angelo, Paola; Della Longa, Stefano; Hodgson, Keith O. (2005). "The Solution Structure of [Cu(aq)]2+ and Its Implications for Rack-Induced Bonding in Blue Copper Protein Active Sites". Inorganic Chemistry 44 (6): 1922–1933. doi:10.1021/ic0400639. PMID 15762718.
- ↑ Senn, Peter (October 1992). "A simple quantum mechanical model that illustrates the Jahn–Teller effect". Journal of Chemical Education 69 (10): 819. doi:10.1021/ed069p819. Bibcode: 1992JChEd..69..819S.
- ↑ Klärner, Frank-Gerrit (2001). "About the Antiaromaticity of Planar Cyclooctatetraene". Angewandte Chemie International Edition in English 40 (21): 3977–3981. doi:10.1002/1521-3773(20011105)40:21<3977::AID-ANIE3977>3.0.CO;2-N.
- ↑ 8.0 8.1 Jahn, H. A.; Teller, E. (1937). "Stability of polyatomic molecules in degenerate electronic states. I. Orbital degeneracy". Proc. R. Soc. A 161 (A905): 220–235. doi:10.1098/rspa.1937.0142. Bibcode: 1937RSPSA.161..220J.
- ↑ Bersuker, I. B. (2006). The Jahn–Teller Effect. Cambridge: Cambridge University Press. ISBN 9780521822121. https://archive.org/details/jahntellereffect0000bers.
- ↑ 10.0 10.1 Bates, C. A. (1978). "Jahn–Teller effects in paramagnetic crystals". Physics Reports 35 (3): 187–304. doi:10.1016/0370-1573(78)90122-9. Bibcode: 1978PhR....35..187B.
- ↑ Englman, R. (1972). The Jahn–Teller Effect in Molecules and Crystals. Wiley-Interscience. ISBN 9780471241683. https://archive.org/details/jahntellereffect0000engl.
- ↑ Van Vleck, J. H. (1939). "On the Magnetic Behavior of Vanadium, Titanium and Chrome Alum". J. Chem. Phys. 7 (1): 61–71. doi:10.1063/1.1750326. Bibcode: 1939JChPh...7...61V.
- ↑ Van Vleck, J. H. (1939). "The Jahn–Teller effect and crystalline stark splitting for clusters of the form XY6". J. Chem. Phys. 7 (1): 72–84. doi:10.1063/1.1750327. Bibcode: 1939JChPh...7...72V.
- ↑ Bleaney, B.; Ingram, D. J. E. (1950). "Paramagnetic Resonance in Copper Fluosilicate". Proc. R. Soc. A 63 (364): 408–409. doi:10.1088/0370-1298/63/4/112. Bibcode: 1950PPSA...63..408B.
- ↑ Bleaney, B.; Bowers, K. D. (1952). "The Cupric ion in a Trigonal Crystalline Electric Field". Proc. R. Soc. A 65 (392): 667–668. doi:10.1088/0370-1298/65/8/111. Bibcode: 1952PPSA...65..667B.
- ↑ 16.0 16.1 Öpik, U.; Pryce, M. H. L. (1957). "Studies of the Jahn Teller Effect.1. A Survey of the Static Problem". Proc. R. Soc. A 238 (1215): 425–447. doi:10.1098/rspa.1957.0010. Bibcode: 1957RSPSA.238..425O.
- ↑ Moffitt, W.; Thorson, W. (1957). "Vibronic States of Octahedral Complexes". Physical Review 108 (5): 1251–1255. doi:10.1103/PhysRev.108.1251. Bibcode: 1957PhRv..108.1251M.
- ↑ Moffitt, W.; Liehr, A. D. (1957). "Configurational Instability of Degenerate Electronic States". Physical Review 106 (6): 1195–1200. doi:10.1103/PhysRev.106.1195. Bibcode: 1957PhRv..106.1195M.
- ↑ 19.0 19.1 Longuet-Higgins, H. C.; Öpik, U.; Pryce, M. H. L.; Sack, R. A. (1958). "Studies of the Jahn–Teller Effect.2. The Dynamical Problem". Proc. R. Soc. A 244 (1236): 1–16. doi:10.1098/rspa.1958.0022. Bibcode: 1958RSPSA.244....1L.
- ↑ Bersuker, I. B. (1963). "Inversion Splitting of Levels in Free Complexes of Transition Metals". Sov. Phys. JETP 16 (4): 933–938. Bibcode: 1963JETP...16..933B.
- ↑ 21.0 21.1 O'Brien, M. C. M. (1964). "Dynamic Jahn–Teller Effect in Octahedrally Co-ordinated d9 Ions". Proc. R. Soc. A 281 (1384): 323–339. doi:10.1098/rspa.1964.0185. Bibcode: 1964RSPSA.281..323O.
- ↑ 22.0 22.1 22.2 Ham, F. S. (1965). "Dynamical Jahn–Teller Effect in Paramagnetic Resonance Spectra – Orbital Reduction Factors and Partial Quenching of Spin–Orbit Interaction". Physical Review 138 (6A): A1727–A1740. doi:10.1103/physrev.138.a1727. Bibcode: 1965PhRv..138.1727H.
- ↑ Berry, M. V. (1984). "Quantal Phase-Factors Accompanying Adiabatic Changes". Proc. R. Soc. A 392 (1802): 45–57. doi:10.1098/rspa.1984.0023. Bibcode: 1984RSPSA.392...45B.
- ↑ Herzberg, G.; Longuet-Higgins, H. C. (1963). "Intersection of Potential Energy Surfaces in Polyatomic Molecules". Discussions of the Faraday Society 35: 77. doi:10.1039/df9633500077.
- ↑ Longuet-Higgins, H. C. (1975). "Intersection of Potential-Energy Surfaces in Polyatomic Molecules". Proc. R. Soc. A 344 (1637): 147–156. doi:10.1098/rspa.1975.0095. Bibcode: 1975RSPSA.344..147L.
- ↑ Mead, C. A.; Truhlar, D. G. (1979). "Determination of Born-Oppenheimer Nuclear Motion Wave-Functions Including Complications due to Conical Intersections and Identical Nuclei". J. Chem. Phys. 70 (5): 2284–2296. doi:10.1063/1.437734. Bibcode: 1979JChPh..70.2284M.
- ↑ Kroto, H. W.; Heath, J. R.; O'Brien, S. C.; Curl, R. F.; Smalley, R. E. (1985). "C60 – Buckminsterfullerene". Nature 318 (6042): 162–163. doi:10.1038/318162a0. Bibcode: 1985Natur.318..162K.
- ↑ Chancey, C. C.; O'Brien, M. C. M (1997). The Jahn–Teller effect in C60 and other icosahedral complexes. Princeton: Princeton University Press. ISBN 9780691044453.
- ↑ Bednorz, J. G.; Müller, K. A. (1986). "Possible High-Tc Superconductivity in the BaLaCuO System". Z. Phys. B 64 (2): 189–193. doi:10.1007/bf01303701. Bibcode: 1986ZPhyB..64..189B.
- ↑ Millis, A. J.; Shraiman, B. I.; Müller, R. (1996). "Dynamic Jahn–Teller effect and colossal magnetoresistance in La1−xSrxMnO3". Phys. Rev. Lett. 77 (1): 175–178. doi:10.1103/PhysRevLett.77.175. PMID 10061800. Bibcode: 1996PhRvL..77..175M.
- ↑ Liehr, A. D. (1963). "Topological Aspects of Conformational Stability Problem .1. Degenerate Electronic States". J. Phys. Chem. 67 (2): 389–+. doi:10.1021/j100796a043.
- ↑ Ham, F. S. (1968). "Effect of Linear Jahn–Teller Coupling on Paramagnetic Resonance in a 2E State". Physical Review 166 (2): 307–321. doi:10.1103/PhysRev.166.307. Bibcode: 1968PhRv..166..307H.
- ↑ Yates, JH; Pitzer, RM (1979). "Molecular and Electronic Structures of Transition Metal Trifluorides". J. Chem. Phys. 70 (9): 4049–4055. doi:10.1063/1.438027. Bibcode: 1979JChPh..70.4049Y.
- ↑ Ridente, Enrico; Hait, Diptarka; Haugen, Eric A.; Ross, Andrew D.; Neumark, Daniel M.; Head-Gordon, Martin; Leone, Stephen R. (2023-05-19). "Femtosecond symmetry breaking and coherent relaxation of methane cations via x-ray spectroscopy" (in en). Science 380 (6646): 713–717. doi:10.1126/science.adg4421. ISSN 0036-8075. https://www.science.org/doi/10.1126/science.adg4421.
- ↑ Deeth, R. J.; Hitchman, M. A. (1985). "Factors Influencing Jahn–Teller Distortions in Six-Coordinate Copper(II) and Low-Spin Nickel(II) Complexes". Inorg. Chem. 25 (8): 1225–1233. doi:10.1021/ic00228a031.
- ↑ Landau, L. D. (1933). "Über die Bewegung der Elektronen in Kristallgitter". Phys. Z. Sowjetunion 3: 644–645.
- ↑ Ganin, A. Y; Takabayashi, Y.; Khimyak, Y. Z.; Margadonna, S.; Tamai, A.; Rosseinsky, M. J; Prassides, K. (2008). "Bulk superconductivity at 38 K in a molecular system". Nat. Mater. 7 (5): 367–71. doi:10.1038/nmat2179. PMID 18425134. Bibcode: 2008NatMa...7..367G.
- ↑ Gunnarsson, O. (1997). "Superconductivity in fullerides". Rev. Mod. Phys. 69 (2): 575–606. doi:10.1103/RevModPhys.69.575. Bibcode: 1997RvMP...69..575G.
- ↑ Zadik, Ruth H.; Takabayashi, Yasuhiro; Klupp, Gyöngyi; Colman, Ross H.; Ganin, Alexey Y.; Potočnik, Anton; Jeglič, Peter; Arčon, Denis et al. (2015). "Optimized unconventional superconductivity in a molecular Jahn–Teller metal". Sci. Adv. 1 (3): 500059. doi:10.1126/sciadv.1500059. PMID 26601168. Bibcode: 2015SciA....1E0059Z.
- ↑ Dunitz, J. D.; Orgel, L. E. (1957). "Electronic properties of transition-metal oxides—I: Distortions from cubic symmetry". J. Phys. Chem. Solids 3 (1): 20–29. doi:10.1016/0022-3697(57)90043-4. Bibcode: 1957JPCS....3...20D.
- ↑ McClure, D. S. (1957). "The distribution of transition metal cations in spinels". J. Phys. Chem. Solids 3 (3–4): 311–317. doi:10.1016/0022-3697(57)90034-3. Bibcode: 1957JPCS....3..311M.
- ↑ Kanamori, J. (1960). "Crystal Distortion in Magnetic Compounds". J. Appl. Phys. 31 (5): S14–S23. doi:10.1063/1.1984590. Bibcode: 1960JAP....31S..14K.
- ↑ Gehring, G. A.; Gehring, K. A. (1975). "Cooperative Jahn–Teller Effects". Rep. Prog. Phys. 38 (1): 1. doi:10.1088/0034-4885/38/1/001. Bibcode: 1975RPPh...38....1G.
- ↑ Kaplan, M. D.; Vekhter, B. G. (1995). Cooperative phenomena in Jahn–Teller crystals. New York: Plenum Press. ISBN 978-1-4615-1859-4.
- ↑ Lee, J. H.; Delaney, K. T.; Bousquet, E.; Spaldin, N. A.; Rabe (2013). "Strong coupling of Jahn–Teller distortion to oxygen-octahedron rotation and functional properties in epitaxially strained orthorhombic LaMnO3". Phys. Rev. B 88 (17): 174426. doi:10.1103/PhysRevB.88.174426. Bibcode: 2013PhRvB..88q4426L.
- ↑ Kugel, K. I.; Khomskii, D. I. (1982). "Jahn–Teller Effect and Magnetism – Transition-Metal Compounds". Sov. Phys. Usp. 25 (4): 231–256. doi:10.3367/UFNr.0136.198204c.0621.
External links
- A series of (mostly biannual) international symposia deal with current problems and modern developments in the field, the most recent of which are
- The conferences are overseen and guided by the international JT steering committee.
- The difference between real rotation and pseudorotation for a fullerene molecule is illustrated here.
 |
