Physics:Rugate filter
A rugate filter, also known as a gradient-index filter, is an optical filter based on a dielectric mirror that selectively reflects specific wavelength ranges of light. This effect is achieved by a periodic, continuous change of the refractive index of the dielectric coating.[2] The word "rugate" is derived from corrugated structures found in nature, which also selectively reflect certain wavelength ranges of light,[3] for example the wings of the Morpho butterfly.[4]
Characteristics
In rugate filters the refractive index varies periodically and continuously as a function of the depth of the mirror coating. This is similar to Bragg mirrors with the difference that the refractive index profile of a Bragg mirror is discontinuous. The refractive index profiles of a Rugate and a Bragg mirror are shown in the graph on the right. In Bragg mirrors, the discontinuous transitions are responsible for reflection of incident light, whereas in rugate filters, incident light is reflected throughout the thickness of the coating. According to the Fresnel equations, however, the reflection coefficient is greatest where the greatest change in refractive index occurs. For rugate filters, these are the inflection points in the refractive index profile. The theory of the Bragg mirror leads to a calculation of the wavelength at which the reflection of a rugate filter is greatest. For an alternating sequence in the Bragg mirror, the maximum reflection at a wavelength [math]\displaystyle{ \lambda_0 }[/math] is:
- [math]\displaystyle{ n_{\rm L}d_{\rm L} + n_{\rm H}d_{\rm H} = \frac{\lambda_0}{2} }[/math]
In this equation [math]\displaystyle{ n_{\rm L} }[/math] and [math]\displaystyle{ n_{\rm H} }[/math] stand for the high and low refractive indices of the Bragg mirror while [math]\displaystyle{ d_{\rm L} }[/math] and [math]\displaystyle{ d_{\rm H} }[/math] are the respective thicknesses of these layers. For the more general case that the refractive index changes continuously, the previous equation can be rewritten as:
- [math]\displaystyle{ \frac{\int_0^d{n(x)}\mathrm{d}x}{d}d = \left \langle n \right \rangle d = \frac{\lambda_0}{2} }[/math]
On the left hand side is the integral over the refractive index over one period of the refractive index profile [math]\displaystyle{ n(x) }[/math] divided by the period length [math]\displaystyle{ d }[/math]. This term corresponds to the mean value of the refractive index profile.[5] As a sanity check for the correctness of this equation, one can solve the integral for a discrete refractive index profile and substitute the period of a Bragg mirror [math]\displaystyle{ d = d_{\rm H} + d_{\rm L} }[/math].
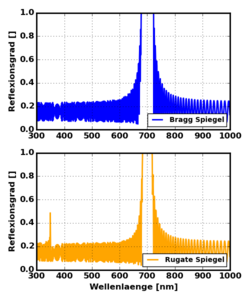
The figure on the right shows the reflection spectra calculated by the transfer-matrix method for the refractive index profiles of a Bragg and Rugate filter. It can be seen that both mirrors have their maximum reflectivity at 700 nm, whereas the rugate filter has a lower bandwidth. For this reason rugate filters are often used as optical notch filters. Furthermore, one can see a smaller peak in the spectrum of the rugate filter at [math]\displaystyle{ \lambda_0/2 }[/math]. This peak is not present in the spectrum of the Bragg mirror because of its discrete layer system, which causes destructive interference at this wavelength. However, Bragg mirrors have secondary maxima at wavelengths of [math]\displaystyle{ \lambda_0/(2n-1) }[/math], which may be undesirable if you only want to filter out a certain wavelength. Rugate filters are better suited for this purpose because the sinusoidal refractive index profile has anti-reflection properties similar to those of black silicon. This reduces the intensity of the secondary maxima.[5]
Production
Rugate filters can be produced by sputtering[6] and chemical vapor deposition.[7] A special challenge is the creation of the continuous refractive index profile. To achieve this, the chemical composition of the mirror must also change continuously as a function of the layer thickness. This can be achieved by continuously changing the gas composition during the deposition process. Another possibility for the production of rugate filters is electrochemical porosification of silicon. Here, the current density during the etching process is selected so that the resulting porosity and thus the refractive index varies sinusoidally with the layer thickness.[8]
References
- ↑ "Porous single crystalline 4H silicon carbide rugate mirrors" (in en). APL Materials 5 (10): 106106. October 2017. doi:10.1063/1.5001876. Bibcode: 2017APLM....5j6106L.
- ↑ "Rugate Filters" (in en). https://www.rp-photonics.com/rugate_filters.html.
- ↑ Thin-film optical filters (3rd ed.). Bristol: Institute of Physics Pub. 2001. ISBN 0-7503-0688-2.
- ↑ "Towards outperforming conventional sensor arrays with fabricated individual photonic vapour sensors inspired by Morpho butterflies". Nature Communications 6 (1): 7959. September 2015. doi:10.1038/ncomms8959. PMID 26324320. Bibcode: 2015NatCo...6.7959P.
- ↑ 5.0 5.1 Optical coatings : material aspects in theory and practice. Heidelberg. 29 April 2014. ISBN 978-3-642-54063-9. OCLC 879593612. https://www.worldcat.org/oclc/879593612.
- ↑ "Graded refractive index layer systems for antireflective coatings and rugate filters deposited by reactive pulse magnetron sputtering" (in en). Surface and Coatings Technology 180-181: 616–620. March 2004. doi:10.1016/j.surfcoat.2003.10.105.
- ↑ "Rugate filters grown by plasma-enhanced chemical vapor deposition" (in en). Thin Solid Films 245 (1–2): 141–145. June 1994. doi:10.1016/0040-6090(94)90889-3. Bibcode: 1994TSF...245..141L.
- ↑ "Photonic crystal sensors based on porous silicon". Sensors 13 (4): 4694–713. April 2013. doi:10.3390/s130404694. PMID 23571671. Bibcode: 2013Senso..13.4694P.
 |  |
