Physics:Schottky anomaly

Schottky anomalous heat capacity [math]\displaystyle{ C }[/math] for a two-level system. [math]\displaystyle{ T }[/math] is the absolute temperature, [math]\displaystyle{ k_\mathrm{B} }[/math] is the Boltzmann constant and [math]\displaystyle{ \varepsilon }[/math] is the energy difference between the levels.

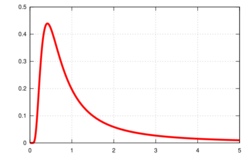
The Schottky anomaly is an effect observed in solid-state physics where the specific heat capacity of a solid at low temperature has a peak. It is called anomalous because the heat capacity usually increases with temperature, or stays constant. It occurs in systems with a limited number of energy levels so that E(T) increases with sharp steps, one for each energy level that becomes available. Since Cv =(dE/dT), it will experience a large peak as the temperature crosses over from one step to the next.

This effect can be explained by looking at the change in entropy of the system. At zero temperature only the lowest energy level is occupied, entropy is zero, and there is very little probability of a transition to a higher energy level. As the temperature increases, there is an increase in entropy and thus the probability of a transition goes up. As the temperature approaches the difference between the energy levels there is a broad peak in the specific heat corresponding to a large change in entropy for a small change in temperature. At high temperatures all of the levels are populated evenly, so there is again little change in entropy for small changes in temperature, and thus a lower specific heat capacity.

[math]\displaystyle{ S = \int_0^T \! \left(\frac{C_{v}}{T}\right)dT \, }[/math]

For a two level system the specific heat coming from the Schottky anomaly has the form:

[math]\displaystyle{ C_{\rm Schottky} = R\left(\frac{\Delta}{T}\right)^{2} \frac{e^{\Delta / T}}{[1 + e^{\Delta / T}]^{2}} \, }[/math]

Where Δ is the energy between the two levels.

This anomaly is usually seen in paramagnetic salts or even ordinary glass (due to paramagnetic iron impurities) at low temperature. At high temperature the paramagnetic spins have many spin states available, but at low temperatures some of the spin states are "frozen out" (having too high energy due to crystal field splitting), and the entropy per paramagnetic atom is lowered.

It was named after Walter H. Schottky.

Details

In a system where particles can have either a state of energy 0 or [math]\displaystyle{ \epsilon }[/math], the expected value of the energy of a particle in the canonical ensemble is:

[math]\displaystyle{ \langle \epsilon \rangle = \epsilon \cdot \frac {e^{-\beta \epsilon}} {1 + e ^ {- \beta \epsilon}} = \frac {\epsilon} {e ^ {+ \beta \epsilon} +1} }[/math]

with the inverse temperature [math]\displaystyle{ \beta = \frac {1} {k_\mathrm{B} T} }[/math] and the Boltzmann constant [math]\displaystyle{ k_\mathrm{B} }[/math].

The total energy of [math]\displaystyle{ N }[/math] independent particles is thus:

[math]\displaystyle{ U = N \langle \epsilon \rangle = \frac {N \epsilon} {e ^ {+ \beta \epsilon} +1} }[/math]

The heat capacity is therefore:

[math]\displaystyle{ C = \left (\frac {\partial U} {\partial T} \right)_\epsilon = - \frac {1} {k_\mathrm{B} T^2} \frac {\partial U} { \partial \beta} = Nk_\mathrm{B} \left (\frac {\epsilon} {k_\mathrm{B} T} \right)^2 \frac {e^{+ \frac {\epsilon} {k_\mathrm{B} T}}} {\left (e ^ {+\frac {\epsilon} {k_\mathrm{B} T}} + 1 \right) ^ 2} }[/math]

Plotting [math]\displaystyle{ C }[/math] as a function of temperature, a peak can be seen at [math]\displaystyle{ k_\mathrm{B}T \approx 0.417 \epsilon }[/math]. In this section [math]\displaystyle{ \frac {\epsilon}{k_\mathrm B} = \Delta }[/math] for the [math]\displaystyle{ \Delta }[/math] in the introductory section.