Physics:Fluxional molecule
In chemistry and molecular physics, fluxional (or non-rigid) molecules are molecules that undergo dynamics such that some or all of their atoms interchange between symmetry-equivalent positions.[1] Because virtually all molecules are fluxional in some respects, e.g. bond rotations in most organic compounds, the term fluxional depends on the context and the method used to assess the dynamics. Often, a molecule is considered fluxional if its spectroscopic signature exhibits line-broadening (beyond that dictated by the Heisenberg uncertainty principle) due to chemical exchange.[2] In some cases, where the rates are slow, fluxionality is not detected spectroscopically, but by isotopic labeling and other methods.[3]
Spectroscopic studies
Many organometallic compounds exhibit fluxionality.[4] Fluxionality is however pervasive.
NMR spectroscopy
Temperature dependent changes in the NMR spectra result from dynamics associated with the fluxional molecules when those dynamics proceed at rates comparable to the frequency differences observed by NMR. The experiment is called DNMR and typically involves recording spectra at various temperatures. In the ideal case, low temperature spectra can be assigned to the "slow exchange limit", whereas spectra recorded at higher temperatures correspond to molecules at "fast exchange limit". Typically, high temperature spectra are simpler than those recorded at low temperatures, since at high temperatures, equivalent sites are averaged out. Prior to the advent of DNMR, kinetics of reactions were measured on non-equilibrium mixtures, monitoring the approach to equilibrium.
Many molecular processes exhibit fluxionality that can be probed on the NMR time scale.[5] Beyond the examples highlighted below, other classic examples include the Cope rearrangement in bullvalene and the chair inversion in cyclohexane.
For processes that are too slow for traditional DNMR analysis, the technique spin saturation transfer (SST, also called EXSY for exchange spectroscopy) is applicable. This magnetization transfer technique gives rate information, provided that the rates exceed 1/T1.[6]
IR spectroscopy
Although less common, some dynamics are also observable on the time-scale of IR spectroscopy. One example is electron transfer in a mixed-valence dimer of metal clusters. Application of the equation for coalescence of two signals separated by 10 cm−1 gives the following result:[7]
Clearly, processes that induce line-broadening on the IR time-scale must be much more rapid than the cases that exchange on the NMR time scale.
Examples
Cyclohexane and related rings

The interconversion of equivalent chair conformers of cyclohexane (and many other cyclic compounds) is called ring flipping. Carbon–hydrogen bonds that are axial in one configuration become equatorial in the other, and vice versa. At room temperature the two chair conformations rapidly equilibrate. The proton- and carbon-13 NMR spectra of cyclohexane show each only singlets near room temperature. At low temperatures, the singlet in the 1H NMR spectrum decoalesces but the 13C NMR spectrum remains unchanged.[9]
Berry pseudorotation of pentacoordinate compounds
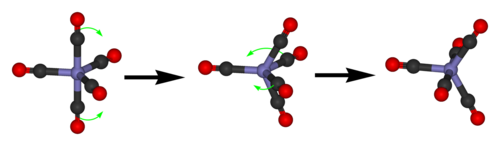
A prototypical fluxional molecule is phosphorus pentafluoride. Its 19F NMR spectrum consists of a 31P-coupled doublet, indicating that the equatorial and axial fluorine centers interchange rapidly on the NMR timescale. Fluorine-19 NMR spectroscopy, even at temperatures as low as −100 °C, fails to distinguish the axial from the equatorial fluorine environments. The apparent equivalency arises from the low barrier for pseudorotation via the Berry mechanism, by which the axial and equatorial fluorine atoms rapidly exchange positions.[10] Iron pentacarbonyl (Fe(CO)5) follows the pattern set for PF5: only one signal is observed in the 13C NMR spectrum near room temperature) whereas at low temperatures, two signals in a 2:3 ratio can be resolved. In sulfur tetrafluoride (SF4), a similar pattern is observed even though this compound has only four ligands.
A well-studied fluxional ion is the methanium ion, which is protonated methane, CH+5.[11][12][13] In this unusual species, whose IR spectrum was experimentally observed[14][12] and understood,[15][16][17] the barriers to proton exchange are lower than the zero-point energy. Thus, even at absolute zero there is no rigid molecular structure; the H atoms are always in motion. More precisely, the spatial distribution of protons in CH+5 is many times broader than its parent molecule CH4, methane.[18][19]
Six-coordinate species
While nonrigidity is common for pentacoordinate species, six-coordinate species typically adopt a more rigid octahedral molecular geometry, featuring close-packed array of six ligating atoms surrounding a central atom. Such compounds do rearrange intramolecularly via the Ray-Dutt twist and the Bailar twist, but the barriers for these processes are typically high such that these processes do not lead to line broadening. For some compounds, dynamics occur via dissociation of a ligand, giving a pentacoordinate intermediate, which is subject to the mechanisms discussed above. Yet another mechanism, exhibited by Fe(CO)4(SiMe3)2 and related hydride complexes, is intramolecular scrambling of ligands over the faces of the tetrahedron defined by the four CO ligands.[20]
Dimethylformamide
A classic example of a fluxional molecule is dimethylformamide (DMF).[21]
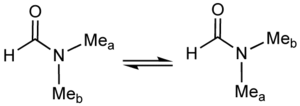
At temperatures near 100 °C, the 500 MHz 1H NMR spectrum of DMF shows only one signal for the methyl groups. Near room temperature however, separate signals are seen for the non-equivalent methyl groups. The rate of exchange can be calculated at the temperature where the two signals are just merged. This "coalescence temperature" depends on the measuring field. The relevant equation is:
where Δνo is the difference in Hz between the frequencies of the exchanging sites. These frequencies are obtained from the limiting low-temperature NMR spectrum. At these lower temperatures, the dynamics continue, of course, but the contribution of the dynamics to line broadening is negligible.
For example, if Δνo = 1ppm @ 500 MHz
- (ca. 0.5 millisecond half-life)
"Ring whizzing"
The compound Fe(η5-C5H5)(η1-C5H5)(CO)2 exhibits the phenomenon of "ring whizzing".
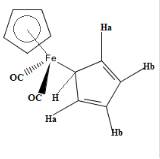
At 30 °C, the 1H NMR spectrum shows only two peaks, one typical (δ5.6) of the η5-C5H5 and the other assigned η1-C5H5. The singlet assigned to the η1-C5H5 ligand splits at low temperatures owing to the slow hopping of the Fe center from carbon to carbon in the η1-C5H5 ligand.[22] Two mechanisms have been proposed, with the consensus favoring the 1,2 shift pathway.[23]
See also
- Pyramidal inversion
- Bullvalene, a fluxional molecule
- Hapticity § Hapticity and fluxionality
- Molecular symmetry § Molecular nonrigidity
- Pseudorotation
Further reading
- D. Papoušek and M. R. Aliev, Molecular Vibrational-Rotational Spectra Elsevier, Amsterdam, 1982</ref><ref>E. B. Wilson, J. C. Decius, and P. C. Cross, Molecular Vibrations, McGraw-Hill, New York, 1955 (Reprinted by Dover 1980)
- Longuet-Higgins, H.C. (1963). "The symmetry groups of non-rigid molecules". Molecular Physics 6 (5): 445–460. doi:10.1080/00268976300100501. Bibcode: 1963MolPh...6..445L.: The use of permutation-inversion groups for the symmetry classification of the states of fluxional (or non-rigid) molecules.
- P. R. Bunker and P. Jensen, Fundamentals of Molecular Symmetry, CRC Press, 1998 ISBN 0-7503-0941-5[1]
- H. W. Kroto, Molecular Rotation Spectra, Wiley, New York, 1975 (Reprinted by Dover 1992), describing the term semi-rigid molecule.
- Philip R. Bunker and Per Jensen, Molecular Symmetry and Spectroscopy, 2nd edition, NRC Research Press, Ottawa, 1998 [2][yes|permanent dead link|dead link}}]
References
- ↑ Fluxional. 2014. doi:10.1351/goldbook.F02463. https://goldbook.iupac.org/terms/view/F02463.
- ↑ Drago, Russell S. (1977). Physical Methods in Chemistry (2nd ed.). Philadelphia: W. B. Saunders. ISBN 0-7216-3184-3.
- ↑ J. Sandström (1982). Dynamic NMR Spectroscopy. Academic Press.
- ↑ John W. Faller "Stereochemical Nonrigidity of Organometallic Complexes" Encyclopedia of Inorganic and Bioinorganic Chemistry 2011, Wiley-VCH, Weinheim. doi:10.1002/9781119951438.eibc0211
- ↑ Bryant, Robert G. (1983). "The NMR time scale". Journal of Chemical Education 60 (11): 933. doi:10.1021/ed060p933. Bibcode: 1983JChEd..60..933B.
- ↑ Jarek, R. L.; Flesher, R. J.; Shin, S. K. (1997). "Kinetics of Internal Rotation of N,N-Dimethylacetamide: A Spin-Saturation Transfer Experiment". Journal of Chemical Education 74 (8): 978. doi:10.1021/ed074p978. Bibcode: 1997JChEd..74..978J.
- ↑ Casey H. Londergan; Clifford P. Kubiak (2003). "Electron Transfer and Dynamic Infrared-Band Coalescence: It Looks Like Dynamic NMR Spectroscopy, but a Billion Times Faster". Chemistry: A European Journal 9 (24): 5969ff. doi:10.1002/chem.200305028. PMID 14679508.
- ↑ J, Clayden (2003). Organic chemistry (2nd ed.). Oxford. pp. 373. ISBN 9780191666216.
- ↑ Gill, G.; Pawar, D. M.; Noe, E. A. (2005). "Conformational Study of cis-1,4-Di-tert-butylcyclohexane by Dynamic NMR Spectroscopy and Computational Methods. Observation of Chair and Twist-Boat Conformations". J. Org. Chem. 70 (26): 10726–10731. doi:10.1021/jo051654z. PMID 16355992.
- ↑ Gutowsky, H. S.; McCall, D. W.; Slichter, C. P. (1953). "Nuclear Magnetic Resonance Multiplets in Liquids". J. Chem. Phys. 21 (2): 279. doi:10.1063/1.1698874. Bibcode: 1953JChPh..21..279G.
- ↑ Kramer, G. M. (1999). "CH5+ Stability and Mass Spectrometry". Science 286 (5442): 1051a–1051. doi:10.1126/science.286.5442.1051a. ISSN 0036-8075.
- ↑ 12.0 12.1 E. T. White; J. Tang; T. Oka (1999). "CH5+: The infrared spectrum observed". Science 284 (5411): 135–7. doi:10.1126/science.284.5411.135. PMID 10102811. Bibcode: 1999Sci...284..135W.
- ↑ Marx, D. (1999). "MOLECULAR SPECTROSCOPY:CH5+: The Cheshire Cat Smiles". Science 284 (5411): 59–61. doi:10.1126/science.284.5411.59. ISSN 0036-8075. Bibcode: 1999Sci...284...59..
- ↑ D. W. Boo; Z. F. Liu; A. G. Suits; J. S. Tse; Y. T. Lee (1995). "Dynamics of Carbonium Ions Solvated by Molecular Hydrogen: CH5+(H2)n (n= 1, 2, 3)". Science 269 (5220): 57–9. doi:10.1126/science.269.5220.57. PMID 17787703. Bibcode: 1995Sci...269...57B.
- ↑ Asvany, O.; Kumar P, P.; Redlich, B.; Hegemann, I.; Schlemmer, S.; Marx, D. (2005). "Understanding the Infrared Spectrum of Bare CH5+". Science 309 (5738): 1219–1222. doi:10.1126/science.1113729. PMID 15994376. Bibcode: 2005Sci...309.1219A.
- ↑ Xiao-Gang Wang; Tucker Carrington Jr (2016). "Calculated rotation-bending energy levels of CH5+ and a comparison with experiment". Journal of Chemical Physics 144 (20): 204304. doi:10.1063/1.4948549. PMID 27250303. Bibcode: 2016JChPh.144t4304W.
- ↑ H. Schmiedt; Per Jensen; S. Schlemmer (2017). "Rotation-vibration motion of extremely flexible molecules - The molecular superrotor". Chemical Physics Letters 672: 34–46. doi:10.1016/j.cplett.2017.01.045. Bibcode: 2017CPL...672...34S.
- ↑ Thompson, KC; Crittenden, DL; Jordan, MJ (2005). "CH5+: Chemistry's chameleon unmasked". J. Am. Chem. Soc. 127 (13): 4954–4958. doi:10.1021/ja0482280. PMID 15796561.
- ↑ For an animation of the dynamics of CH5+, see http://www.theochem.ruhr-uni-bochum.de/research/marx/topic4b.en.html
- ↑ Vancea, L.; Bennett, M. J.; Jones, C. E.; Smith, R. A.; Graham, W. A. G. (1977). "Stereochemically Nonrigid Six-Coordinate Metal Carbonyl Complexes. 1. Polytopal Rearrangement and X-Ray Structure of Tetracarbonylbis(trimethylsilyl)iron". Inorganic Chemistry 16 (4): 897–902. doi:10.1021/ic50170a035.
- ↑ H. S. Gutowsky; C. H. Holm (1956). "Rate Processes and Nuclear Magnetic Resonance Spectra. II. Hindered Internal Rotation of Amides". J. Chem. Phys. 25 (6): 1228–1234. doi:10.1063/1.1743184. Bibcode: 1956JChPh..25.1228G.
- ↑ Bennett, Jr. M. J.; Cotton, F. A.; Davison, A.; Faller, J. W.; Lippard, S. J.; Morehouse, S. M. (1966). "Stereochemically Nonrigid Organometallic Compounds. I. π-Cyclopentadienyliron Dicarbonyl σ-Cyclopentadiene". J. Am. Chem. Soc. 1966 (88): 4371. doi:10.1021/ja00971a012.
- ↑ Robert B. Jordan, Reaction Mechanisms of Inorganic and Organometallic Systems (Topics in Inorganic Chemistry), 2007. ISBN 978-0195301007
