Physics:Shape control in nanocrystal growth

Short description: Influences on the shape of small crystals

Examples of different nanocrystal shapes

Shape control in nanocrystal growth is the control of the shape of nanocrystals (crystalline nanoparticles) formed in their synthesis by means of varying reaction conditions. This is a concept studied in nanosciences, which is a part of both chemistry and condensed matter physics. There are two processes involved in the growth of these nanocrystals. Firstly, volume Gibbs free energy of the system containing the nanocrystal in solution decreases as the nanocrystal size increases. Secondly, each crystal has a surface Gibbs free energy that can be minimized by adopting the shape that is energetically most favorable. Surface energies of crystal planes are related to their Miller indices, which is why these can help predict the equilibrium shape of a certain nanocrystal.

Because of these two different processes, there are two competing regimes in which nanocrystal growth can take place: the kinetic regime, where the crystal growth is controlled by minimization of the volume free energy, and the thermodynamic regime, where growth is controlled by minimization of the surface free energy. High concentration, low temperatures and short aging times favor the kinetic regime, whereas low concentration, high temperatures and long aging times favor the thermodynamic regime.

The different regimes lead to different shapes of the nanocrystals: the kinetic regime gives anisotropic shapes, whereas the thermodynamic regime gives equilibrium, isotropic shapes, which can be determined using the Wulff construction.

The shape of the nanocrystal determines many properties of the nanocrystal, such as the band gap and polarization of emitted light.

Miller indices and surface energy

The surface energy of a solid is the free energy per unit area of its surface. It equals half the energy per unit area needed for cutting a larger piece of solid in two parts along the surface under examination. This costs energy because chemical bonds are broken. Typically, materials are considered to have one specific surface energy. However, in the case of crystals, the surface energy depends on the orientation of the surface with respect to the unit cell. Different facets of a crystal thus often have different surface energies. This can be understood from the fact that in non-crystalline materials, the building blocks that make up the material (e.g., atoms or molecules) are spread in a homogeneous manner. On average, the same number of bonds needs to be broken, so the same energy per unit area is needed, to create any surface. In crystals, surfaces exhibit a periodic arrangement of particles which is dependent on their orientation. Different numbers of bonds with different bond strengths are broken in the process of creating surfaces along different planes of the material, which causes the surface energies to be different. The type of plane is most easily described using the orientation of the surface with respect to a given unit cell that is characteristic of the material.

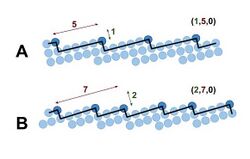
The orientation of a plane with respect to the unit cell is most conveniently expressed in terms of Miller indices. For example, the set of Miller indices (110) describes the set of parallel planes (family of lattice planes) parallel to the z-axis and cutting the x- and the y-axis once, such that every unit cell is bisected by precisely one of those planes in the x- and y-direction.

An example of two surfaces with different surface free energies. Since atoms on a corner have less neighbours than atoms on a terrace, the surface energy of surface B is higher than that of surface A.

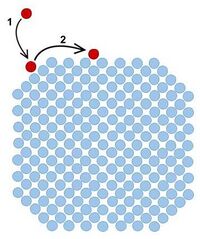
Generally, a surface with high Miller indices has a high surface energy. Qualitatively, this follows from the fact that for higher Miller indices, on average more surface atoms are at positions at a corner instead of a terrace, as can be seen in the figure. After all, corner atoms have even fewer neighbours to interact with than terrace atoms. For example, in the case of a 2D square lattice, they have two instead of three neighbours. These additionally broken bonds all cost energy, which is why lower Miller indices planes generally have lower surface energies and are as a consequence more stable. However, the comparison is in fact somewhat more complex, as the surface energy as function of the Miller indices also depends on the structure of the crystal lattice (e.g., bcc or fcc) and bonds between non-next nearest neighbours play a role as well.

Experimental research on noble metals (copper, gold and silver), shows that for these materials, the surface energy is well-approximated by taking only the nearest neighbours into account. The next-nearest neighbour interactions apparently do not play a major role in these metals. Also, breaking any of the nearest neighbour bonds turns out to cost the same amount of energy. Within this approximation, the surface energy of a certain Miller indices (hkl) surface is given by

[math]\displaystyle{ \gamma_{hkl} = \frac{N_{hkl}}{3} \gamma_{111} }[/math]

with [math]\displaystyle{ \frac{N_{hkl}}{3} }[/math] the ratio of the number of bonds broken when making this (hkl) plane with respect to making a (111) plane, and [math]\displaystyle{ \gamma_{111} }[/math] the surface energy of the (111) plane.

For any surface of an fcc crystal, [math]\displaystyle{ N_{hkl} }[/math] is given by

[math]\displaystyle{ N_{hkl} = \begin{cases} 2h+k & \text{if }h,k,l\text{ are all odd} \\ 4h+2k & \text{otherwise} \end{cases} }[/math]

assuming [math]\displaystyle{ h \geq k \geq l }[/math]. In this model, the surface energy indeed increases with higher Miller indices. This is also visible in the following table, which lists computer simulated surface energies of some planes in copper (Cu), silver (Ag) and gold (Au). Again, [math]\displaystyle{ N_{hkl} }[/math] is the number of broken bonds between nearest neighbours created when making the surface, being 3 for the (111) plane. The surface energy indeed increases for a larger number of broken bonds and therefore larger Miller indices.

Table 1: Surface energies in eV/(surface atom) of noble metals by Miller indices and number of broken bonds

	Cu	Ag	Au	[math]\displaystyle{ N_{hkl} }[/math]
(111)	0.675	0.566	0.623	3
(100)	0.874	0.728	0.842	4
(110)	1.327	1.113	1.284	6
(311)	1.564	1.309	1.468	7
(331)	2.016	1.680	1.900	9
(210)	2.240	1.864	2.149	10
(211)	2.255	1.877	2.110	10

It is also possible for surfaces with high Miller indices to have a low surface energy, mainly if the unit cell contains multiple atoms. After all, Miller indices are based on the unit cell, and it is the atoms, not the unit cell, that are physically present. The choice of unit cell is up to some level arbitrary as they are constructed by the interpreter. High Miller indices planes with low surface energy can be found by searching for planes with a high density of atoms. A large density of atoms in a plane after all implies a large number of in-plane bonds and thus a small number of out-of-plane bonds that would cause the surface energy to be large. If a crystal's unit cell contains only one atom, those planes naturally correspond to the planes with low Miller indices, which is why planes with low Miller indices are usually considered to have a low surface energy.

The table below shows examples of computer simulated surface energies of (hk0) planes in a NiO crystal (with [math]\displaystyle{ h \leq k }[/math]). In this case, the unit cell has a multi-atom basis, as there are two types of atoms that make up the crystal (nickel and oxygen). The data has been ordered by increasing surface energy. From this table, it is clearly visible that the trend between surface energy and Miller indices is not as straightforward in this case as for the noble metals discussed above.

Table 2: Surface energies of NiO by Miller indices

(hk0)	Surface Energy (J/m2)	Surface Energy (kBT/nm2)
(010)	1.170	284.4
(1 14 0)	1.425	346.4
(1 10 0)	1.521	369.7
(170)	1.661	403.7
(160)	1.731	420.8
(150)	1.824	443.4
(290)	1.898	461.4
(140)	1.979	481.0
(270)	2.082	506.1
(130)	2.212	537.7
(250)	2.380	578.5
(370)	2.447	594.8
(490)	2.483	603.5
(120)	2.603	632.7
(470)	2.763	671.6
(350)	2.822	686.0
(580)	2.872	698.1
(230)	2.950	717.1
(570)	3.034	737.5
(340)	3.092	751.6
(790)	3.134	761.8
(450)	3.167	769.8
(560)	3.214	781.2
(670)	3.245	788.8
(110)	3.409	828.6

Surface energy and Equilibrium shape

Planes with low surface energies are relatively stable and thus tend to be predominantly present in the thermodynamic equilibrium shape of a crystal. After all, in equilibrium, the free energy is minimized. However, a crystal's thermodynamic equilibrium shape typically does not only consist of planes with the lowest possible surface energy. The reason for this is that involving planes with a slightly higher surface energy can decrease the total surface area, which lowers the total energy penalty for creating the material's surface. The optimum shape in terms of free energy can be determined by the Wulff construction.

Thermodynamic versus kinetic control

(1) Deposition of a monomer onto a high energy facet. (2) Surface diffusion of the monomer to a lower energy facet in order to reduce the surface free energy.

In the thermodynamic regime, product A is obtained, because growth is driven by minimization of surface Gibbs free energy. In the kinetic regime, product B is obtained, because growth is driven by minimization of volume Gibbs free energy.

The growth of crystals can be carried out under two different regimes: the thermodynamic and the kinetic regime. Research on this topic is mainly centered around nanocrystals, as their synthesis is not as straightforward as that of bulk materials and thus requires a deeper understanding of types of crystal growth. Due to the high surface-volume ratio and the resulting instability, nanocrystals most easily show the difference between the thermodynamic and kinetic regime. These concepts can however be generalized further to bulk material.

A commonly used production method of nanocrystals is that of growth by monomer addition. A seed is formed or placed in a solution of monomers that are the building blocks of the crystal. The nanocrystal (seed) grows larger by consuming the monomers in solution. The addition of a monomer to the crystal happens at the highest energy facet of the crystal, since that is the most active site and the monomer deposition thus has the lowest activation energy there. Usually, this facet is situated at a corner of the nanoparticle. These facets however, as explained in the section above, are not the most energetically favorable position for the added monomer. Thus the monomer will, if it gets the chance to, diffuse along the crystal surface to a lower energy site.

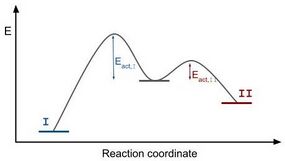
The regime in which the monomers have the time to relocate is called the thermodynamic regime, as the product is formed that is expected thermodynamically. In the kinetic regime, the addition of monomers happens so rapidly that the crystal continues growing at the corners. In this case, the formed product is not at a global minimum of the free energy, but is in a metastable anisotropic state.

Thermodynamic regime

The thermodynamic regime is characterized by relatively low growth rates. Because of these, the amount the Gibbs free energy is lowered due to incorporating a new monomer is smaller than due to rearranging the surface. The former is associated with the minimization of volume Gibbs free energy, whereas the latter is associated with minimizing the surface free energy. Thus, the shape evolution is driven by minimization of surface Gibbs free energy, and therefore the equilibrium shape is the one with the lowest overall surface Gibbs free energy. This corresponds to the shape with a global minimum in Gibbs free energy, which can be obtained via the Wulff construction. From this Wulff construction, it also follows that the thermodynamic product is always symmetrical.

The activation energy for the thermodynamic product is higher than the activation energy for the kinetic product. From the Arrhenius equation [math]\displaystyle{ k = A e^{-E_{act}/k_BT} }[/math] with [math]\displaystyle{ k }[/math] the reaction rate, [math]\displaystyle{ A }[/math] a constant, [math]\displaystyle{ E_{act} }[/math] the activation energy, [math]\displaystyle{ k_B }[/math] the Boltzmann constant and [math]\displaystyle{ T }[/math] the temperature, follows that for overcoming a higher activation energy barrier, a higher temperature is needed. The thermodynamic regime is therefore associated with high temperature conditions.

The thermodynamic regime can also be characterized by giving the system a sufficiently long time to rearrange its atoms such that the global minimum in Gibbs free energy of the entire system is reached. Raising the temperature has a similar effect because the extra thermal energy increases the mobility of the atoms on the surface, making rearrangements easier.

Finally, the thermodynamic product can be obtained by having a low monomer concentration. This too ties into the longer time the system has at hand to rearrange before incorporating the next monomer at a lower monomer concentration, as the speed of diffusion of monomers through the solution to the crystal is strongly dependent on their concentration.

The law of Arrhenius dictates that even though the kinetic product (II) lies higher in total free energy than the thermodynamic product (I) does, the smaller activation energy of the kinetic reaction can result in the kinetic product being the predominant end product.

Kinetic regime

The kinetic control regime is characterized by high growth rates. Due to these, the system is driven by lowering the volume Gibbs free energy, which decreases rapidly upon monomer consumption. Minimization of the surface Gibbs free energy is of less relevance to the system and the shape evolution is controlled by reaction rates instead. Thus the product obtained in this regime is a metastable state, with a local minimum in Gibbs free energy.

Kinetic control is obtained when there is not enough time for atoms on the surface to diffuse to an energetically more favorable state. Conditions that favor kinetic control are low temperatures (to ensure thermal energy is smaller than activation energy of the thermodynamic reaction) and high monomer concentration (in order to obtain high growth rates). Because of the high concentrations needed for kinetic control, the diffusion spheres around the nanocrystal are small and have steep concentration gradients. The more extended parts of the crystal that reach out further through the diffusion sphere grow faster, because they reach parts of the solution where the concentration is higher. The extended facets thus grow even faster, which can result in an anisotropic product. Due to this effect, an important factor determining the final shape of the product is the shape of the initial seed.

Consequences of shape and size

The band gap as well as the density of states of nanoparticles depend significantly on their shape and size. Generally, smaller nanoparticles have a larger band gap. Quantum confinement effects lie at the basis of this. Whereas the density of states is a smooth function for 3D crystals which are large in any direction, it becomes saw-tooth-shaped for 2D nanocrystals (e.g., disks), staircase-shaped for 1D nanocrystals (e.g., wires) and a delta function for 0D nanocrystals (balls, pyramids etc.).

Also, the polarization of emitted light and its magnetic anisotropy are affected by the shape of the nanoparticle.

Studying different shapes of nanoparticles can improve the understanding of quantum confinement effects. By elongating an axis in certain spherical nanoparticles (quantum dots), degeneracies in the energy levels can be resolved. Also, the energy difference between photon absorption and photon emission can be tuned using shape control. This could possibly be utilized in LED technology, as it helps to prevent re-adsorption.