Physics:Sherman function

From HandWiki
Schematic view of Mott scattering. An incident electron beam collides with the target and the electrons scattered to the left and to the right at a specific angle θ are detected

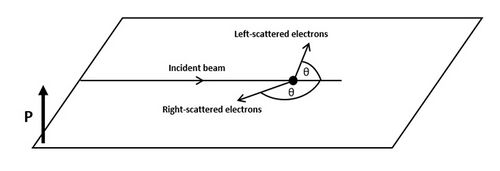
The Sherman function describes the dependence of electron-atom scattering events on the spin of the scattered electrons.[1] It was first evaluated theoretically by the physicist Noah Sherman and it allows the measurement of polarization of an electron beam by Mott scattering experiments.[2] A correct evaluation of the Sherman function associated to a particular experimental setup is of vital importance in experiments of spin polarized photoemission spectroscopy, which is an experimental technique which allows to obtain information about the magnetic behaviour of a sample.[3]

Background

Polarization and spin-orbit coupling

Correction to Coulomb potential due to spin-orbit coupling. The Coulomb potential, result of the interaction of the electron with the charged nucleus is shown in green. The new potential for spin up (blue) and spin down (red) electrons are shown after spin-orbit correctios have been taken into account

When an electron beam is polarized, an unbalance between spin-up, [math]\displaystyle{ n_{up} }[/math], and spin-down electrons, [math]\displaystyle{ n_{down} }[/math], exists. The unbalance can be evaluated through the polarization [math]\displaystyle{ P }[/math] [4] defined as

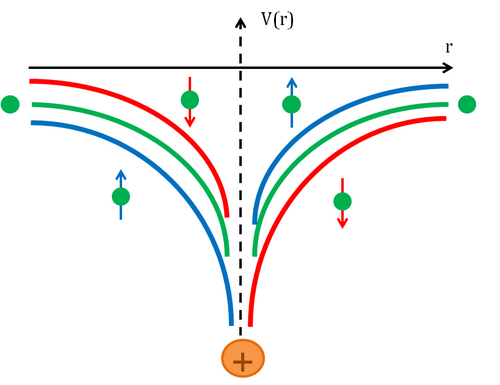
[math]\displaystyle{ P = \frac{n_{up}-n_{down}}{n_{up}+n_{down}} }[/math].

It is known that, when an electron collides against a nucleus, the scattering event is governed by Coulomb interaction. This is the leading term in the Hamiltonian, but a correction due to spin-orbit coupling can be taken into account and the effect on the Hamiltonian can be evaluated with the perturbation theory. Spin orbit interaction can be evaluated, in the rest reference frame of the electron, as the result of the interaction of the spin magnetic moment of the electron

[math]\displaystyle{ \boldsymbol{\mu}_S = -g_\text{s} \mu_\text{B} \frac{\mathbf{S}}{\hbar}, }[/math]

with the magnetic field that the electron sees, due to its orbital motion around the nucleus, whose expression in the non-relativistic limit is:

[math]\displaystyle{ \mathbf{B} = \frac{1}{m_\text{e} ec^2} \frac{1}{r} \frac{\partial U(r)}{\partial r} \mathbf{L}. }[/math]

In these expressions [math]\displaystyle{ \mathbf{S} }[/math] is the spin angular-momentum, [math]\displaystyle{ \mu_\text{B} }[/math] is the Bohr magneton, [math]\displaystyle{ g_\text{s} }[/math] is the g-factor, [math]\displaystyle{ \hbar }[/math] is the reduced Planck constant, [math]\displaystyle{ m_\text{e} }[/math] is the electron mass, [math]\displaystyle{ e }[/math] is the elementary charge, [math]\displaystyle{ c }[/math] is the speed of light, [math]\displaystyle{ U = eV }[/math] is the potential energy of the electron and [math]\displaystyle{ \mathbf{L} = \mathbf{r} \times \mathbf{p} }[/math] is the angular momentum.

Due to spin orbit coupling, a new term will appear in the Hamiltonian, whose expression is[5][page needed]

[math]\displaystyle{ V_\text{SO} = \boldsymbol{\mu_s}\cdot\mathbf{B} }[/math].

Due to this effect, electrons will be scattered with different probabilities at different angles. Since the spin-orbit coupling is enhanced when the involved nuclei possess a high atomic number Z, the target is usually made of heavy metals, such as mercury,[1] gold[6] and thorium.[7]

Asymmetry

If we place two detectors at the same angle from the target, one on the right and one on the left, they will generally measure a different number of electrons [math]\displaystyle{ n_{R} }[/math] and [math]\displaystyle{ n_{L} }[/math]. Consequently it is possible to define the asymmetry [math]\displaystyle{ A }[/math], as[2]

[math]\displaystyle{ A = \frac{n_{R}-n_{L}}{n_{R}+n_{L}} }[/math].
Sherman function as a function of the angle for mercury (Z = 80) with β = 0.2. Typically detectors are placed in a position where the effect is maximized, 120° for gold and mercury[1]

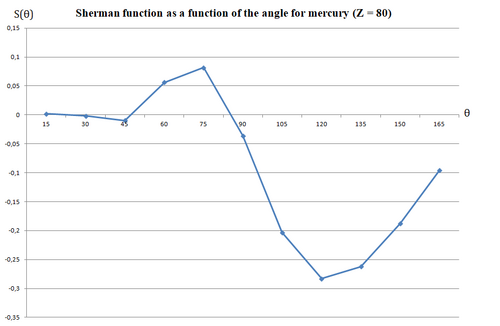
The Sherman function [math]\displaystyle{ S(\theta) }[/math] is a measure of the probability of a spin-up electron to be scattered, at a specific angle [math]\displaystyle{ \theta }[/math], to the right or to the left of the target, due to spin-orbit coupling.[8][9] It can assume values ranging from -1 (spin-up electron is scattered with 100% probability to the left of the target) to +1 (spin-up electron is scattered with 100% probability to the right of the target). The value of the Sherman function depends on the energy of the incoming electron, evaluated via the parameter [math]\displaystyle{ \beta = \frac{v}{c} }[/math].[1] When [math]\displaystyle{ S(\theta)=0 }[/math], spin-up electrons will be scattered with the same probability to the right and to the left of the target.[1]

Then it is possible to write

[math]\displaystyle{ n_{R} = \frac{n_{up}[1+S(\theta)]+n_{down}[1-S(\theta)]}{2} }[/math]
[math]\displaystyle{ n_{L} = \frac{n_{up}[1-S(\theta)]+n_{down}[1+S(\theta)]}{2}. }[/math]

Plugging these formulas inside the definition of asymmetry, it is possible to obtain a simple expression for the evaluation of the asymmetry at a specific angle [math]\displaystyle{ \theta }[/math],[10] i.e.:

[math]\displaystyle{ A = PS(\theta) }[/math].

Theoretical calculations are available for different atomic targets[1][11] and for a specific target, as a function of the angle.[8]

Application

Mott scattering of an electron beam with [math]\displaystyle{ S(\theta)=0.5 }[/math]

To measure the polarization of an electron beam, a Mott detector is required.[12] In order to maximize the spin-orbit coupling, it is necessary that the electrons arrive near to the nuclei of the target. To achieve this condition, a system of electron optics is usually present, in order to accelerate the beam up to keV[13] or to MeV[14] energies. Since standard electron detectors count electrons being insensitive to their spin,[15] after the scattering with the target any information about the original polarization of the beam is lost. Nevertheless, by measuring the difference in the counts of the two detectors, the asymmetry can be evaluated and, if the Sherman function is known from previous calibration, the polarization can be calculated by inverting the last formula.[10]

In order to characterize completely the in-plane polarization, setups are available, with four channeltrons, two devoted to the left-right measure and two devoted to the up-right measure.[7]

Example

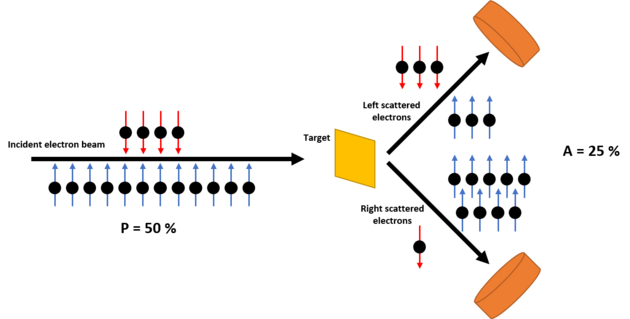
In the panel it is shown an example of the working principle of a Mott detector, supposing a value for [math]\displaystyle{ S(\theta)=0.5 }[/math]. If an electron beam with a 3:1 ratio of spin-up over spin-down electrons collide with the target, it will be splitted with a ratio 5:3, according to previous equation, with an asymmetry of 25%.

See also

References

  1. ↑ 1.0 1.1 1.2 1.3 1.4 1.5 Sherman, Noah (15 September 1956). "Coulomb Scattering of Relativistic Electrons by Point Nuclei". Physical Review 103 (6): 1601–1607. doi:10.1103/physrev.103.1601. Bibcode: 1956PhRv..103.1601S. 
  2. ↑ 2.0 2.1 Mott, Nevill Francis (January 1997). "The scattering of electrons by atoms.". Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 127 (806): 658–665. doi:10.1098/rspa.1930.0082. 
  3. ↑ Nishide, Akinori; Takeichi, Yasuo; Okuda, Taichi; Taskin, Alexey A; Hirahara, Toru; Nakatsuji, Kan; Komori, Fumio; Kakizaki, Akito et al. (17 June 2010). "Spin-polarized surface bands of a three-dimensional topological insulator studied by high-resolution spin- and angle-resolved photoemission spectroscopy". New Journal of Physics 12 (6): 065011. doi:10.1088/1367-2630/12/6/065011. Bibcode: 2010NJPh...12f5011N. 
  4. ↑ Mayne, K. I. (July 1969). "Polarized electron beams". Contemporary Physics 10 (4): 387–412. doi:10.1080/00107516908204794. Bibcode: 1969ConPh..10..387M. 
  5. ↑ Griffiths, Davis J.. Introduction to quantum mechanics (2nd ed.). Pearson Prentice Hall. ISBN 0131118927. 
  6. ↑ Ciullo, Giuseppe; Contalbrigo, Marco; Lenisa, Paolo (2009). Polarized Sources, Targets and Polarimetry : Proceedings of the 13th International Workshop.. World Scientific Publishing Co Pte Ltd. pp. 337. ISBN 9781283148580. 
  7. ↑ 7.0 7.1 Berti, G.; Calloni, A.; Brambilla, A.; Bussetti, G.; Duò, L.; Ciccacci, F. (July 2014). "Direct observation of spin-resolved full and empty electron states in ferromagnetic surfaces". Review of Scientific Instruments 85 (7): 073901. doi:10.1063/1.4885447. PMID 25085146. Bibcode: 2014RScI...85g3901B. 
  8. ↑ 8.0 8.1 Chao, Alexander W.; Mess, Karl H. (2013). Handbook of accelerator physics and engineering (Second ed.). World scientific. pp. 756–757. ISBN 978-9814415859. 
  9. ↑ Joachim, Kessler (1976). Polarized electrons. Springer-Verlag. p. 49. ISBN 978-3-662-12721-6. 
  10. ↑ 10.0 10.1 Sherman, Noah; Nelson, Donald F. (15 June 1959). "Determination of Electron Polarization by Means of Mott Scattering". Physical Review 114 (6): 1541–1542. doi:10.1103/PhysRev.114.1541. Bibcode: 1959PhRv..114.1541S. 
  11. ↑ Czyżewski, Zbigniew; MacCallum, Danny O’Neill; Romig, Alton; Joy, David C. (October 1990). "Calculations of Mott scattering cross section". Journal of Applied Physics 68 (7): 3066–3072. doi:10.1063/1.346400. Bibcode: 1990JAP....68.3066C. 
  12. ↑ Nelson, D. F.; Pidd, R. W. (1 May 1959). "Measurement of the Mott Asymmetry in Double Scattering of Electrons". Physical Review 114 (3): 728–735. doi:10.1103/PhysRev.114.728. Bibcode: 1959PhRv..114..728N. 
  13. ↑ Petrov, V. N.; Landolt, M.; Galaktionov, M. S.; Yushenkov, B. V. (December 1997). "A new compact 60 kV Mott polarimeter for spin polarized electron spectroscopy". Review of Scientific Instruments 68 (12): 4385–4389. doi:10.1063/1.1148400. Bibcode: 1997RScI...68.4385P. 
  14. ↑ Steigerwald, M.. "MeV Mott Polarimetry at Jefferson Lab". https://www.jlab.org/accel/inj_group/mott/mott.pdf. Retrieved 25 June 2020. 
  15. ↑ Ladislas Wiza, Joseph (June 1979). "Microchannel plate detectors". Nuclear Instruments and Methods 162 (1–3): 587–601. doi:10.1016/0029-554X(79)90734-1. Bibcode: 1979NucIM.162..587L. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Sherman_function&oldid=3280464"