Physics:Superradiant phase transition

Short description: Process in quantum optics

Schematic plot of the order parameter of the Dicke transition, which is zero in the normal phase and finite in the superradiant phase. The inset shows the free energy in the normal and superradiant phases

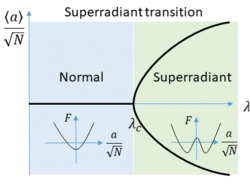
In quantum optics, a superradiant phase transition is a phase transition that occurs in a collection of fluorescent emitters (such as atoms), between a state containing few electromagnetic excitations (as in the electromagnetic vacuum) and a superradiant state with many electromagnetic excitations trapped inside the emitters. The superradiant state is made thermodynamically favorable by having strong, coherent interactions between the emitters.

The superradiant phase transition was originally predicted by the Dicke model of superradiance, which assumes that atoms have only two energetic levels and that these interact with only one mode of the electromagnetic field. The phase transition occurs when the strength of the interaction between the atoms and the field is greater than the energy of the non-interacting part of the system. (This is similar to the case of superconductivity in ferromagnetism, which leads to the dynamic interaction between ferromagnetic atoms and the spontaneous ordering of excitations below the critical temperature.) The collective Lamb shift, relating to the system of atoms interacting with the vacuum fluctuations, becomes comparable to the energies of atoms alone, and the vacuum fluctuations cause the spontaneous self-excitation of matter.

The transition can be readily understood by the use of the Holstein-Primakoff transformation applied to a two-level atom. As a result of this transformation, the atoms become Lorentz harmonic oscillators with frequencies equal to the difference between the energy levels. The whole system then simplifies to a system of interacting harmonic oscillators of atoms, and the field known as Hopfield dielectric which further predicts in the normal state polarons for photons or polaritons. If the interaction with the field is so strong that the system collapses in the harmonic approximation and complex polariton frequencies (soft modes) appear, then the physical system with nonlinear terms of the higher order becomes the system with the Mexican hat-like potential, and will undergo ferroelectric-like phase transition. In this model, the system is mathematically equivalent for one mode of excitation to the Trojan wave packet, when the circularly polarized field intensity corresponds to the electromagnetic coupling constant. Above the critical value, it changes to the unstable motion of the ionization.

The superradiant phase transition was the subject of a wide discussion as to whether or not it is only a result of the simplified model of the matter-field interaction; and if it can occur for the real physical parameters of physical systems (a no-go theorem). However, both the original derivation and the later corrections leading to nonexistence of the transition – due to Thomas–Reiche–Kuhn sum rule canceling for the harmonic oscillator the needed inequality to impossible negativity of the interaction – were based on the assumption that the quantum field operators are commuting numbers, and the atoms do not interact with the static Coulomb forces. This is generally not true like in case of Bohr–van Leeuwen theorem and the classical non-existence of Landau diamagnetism. The negating results were also the consequence of using the simple Quantum Optics models of the electromagnetic field-matter interaction but not the more realistic Condenced Matter models like for example the superconductivity model of the BCS but with the phonons replaced by photons to first obtain the collective polaritons. The return of the transition basically occurs because the inter-atom dipole-dipole or generally the electron-electron Coulomb interactions are never negligible in the condensed and even more in the superradiant matter density regime and the Power-Zienau unitary transformation eliminating the quantum vector potential in the minimum-coupling Hamiltonian transforms the Hamiltonian exactly to the form used when it was discovered and without the square of the vector potential which was later claimed to prevent it. Alternatively within the full quantum mechanics including the electromagnetic field the generalized Bohr–van Leeuwen theorem does not work and the electromagnetic interactions cannot be eliminated while they only change the [math]\displaystyle{ \mathbf{p} \cdot \mathbf{A} }[/math] vector potential coupling to the electric field [math]\displaystyle{ \mathbf{x} \cdot \mathbf{E} }[/math] coupling and alter the effective electrostatic interactions. It can be observed in model systems like Bose–Einstein condensates and artificial atoms.

Theory

Criticality of linearized Jaynes-Cummings model

A superradiant phase transition is formally predicted by the critical behavior of the resonant Jaynes-Cummings model, describing the interaction of only one atom with one mode of the electromagnetic field. Starting from the exact Hamiltonian of the Jaynes-Cummings model at resonance

[math]\displaystyle{ \hat{H}_{\text{JC}} = \hbar \omega \hat{a}^{\dagger}\hat{a} +\hbar \omega \frac{\hat{\sigma}_z}{2} +\frac{\hbar \Omega}{2} \left(\hat{a}\hat{\sigma}_+ +\hat{a}^{\dagger}\hat{\sigma}_- +\hat{a}\hat{\sigma}_- +\hat{a}^{\dagger}\hat{\sigma}_+\right), }[/math]

Applying the Holstein-Primakoff transformation for two spin levels, replacing the spin raising and lowering operators by those for the harmonic oscillators

[math]\displaystyle{ \hat{\sigma}_- \approx \hat{b} }[/math]

[math]\displaystyle{ \hat{\sigma}_+\approx \hat{b}^{\dagger} }[/math]

[math]\displaystyle{ \hat{\sigma}_z\approx 2 \hat{b}^{\dagger}\hat{b} }[/math]

one gets the Hamiltonian of two coupled harmonic-oscillators:

[math]\displaystyle{ \hat{H}_{\text{JC}} = \hbar \omega \hat{a}^{\dagger}\hat{a} +\hbar \omega \hat{b}^{\dagger}\hat{b} +\frac{\hbar \Omega}{2} \left(\hat{a}\hat{b}^{\dagger} +\hat{a}^{\dagger}\hat{b} +\hat{a}\hat{b} +\hat{a}^{\dagger}\hat{b}^{\dagger} \right), }[/math]

which readily can be diagonalized. Postulating its normal form

[math]\displaystyle{ \hat{H}_{\text{JC}}=\Omega_+ \hat{A_+}^{\dagger}\hat{A_+}+\Omega_- \hat{A_-}^{\dagger}\hat{A_-}+C }[/math]

where

[math]\displaystyle{ \hat{A_{\pm}}=c_{\pm1} \hat{a} + c_{\pm2} \hat{a}^{\dagger} + c_{\pm3} \hat{b} + c_{\pm4} \hat{b}^{\dagger} }[/math]

one gets the eigenvalue equation

[math]\displaystyle{ [\hat{A_{\pm}},\hat{H}_{\text{JC}}]=\Omega_{\pm}A }[/math]

with the solutions

[math]\displaystyle{ \Omega_{\pm}=\omega \sqrt{1 \pm \frac{\Omega}{\omega}} }[/math]

The system collapses when one of the frequencies becomes imaginary, i.e. when

[math]\displaystyle{ \Omega\gt \omega }[/math]

or when the atom-field coupling is stronger than the frequency of the mode and atom oscillators. While there are physically higher terms in the true system, the system in this regime will therefore undergo the phase transition.

Criticality of Jaynes-Cummings model

The simplified Hamiltonian of the Jaynes-Cummings model, neglecting the counter-rotating terms, is

[math]\displaystyle{ \hat{H}_{\text{JC}} = \hbar \omega \hat{a}^{\dagger}\hat{a} +\hbar \omega \frac{\hat{\sigma}_z}{2} +\frac{\hbar \Omega}{2} \left(\hat{a}\hat{\sigma}_+ +\hat{a}^{\dagger}\hat{\sigma}_-\right), }[/math]

and the energies for the case of zero detuning are

[math]\displaystyle{ E_{\pm}(n) = \hbar\omega \left(n+\frac{1}{2}\right) \pm \frac{1}{2} \hbar\Omega(n), }[/math]

[math]\displaystyle{ \Omega(n) = \Omega \sqrt{n+1} }[/math]

where [math]\displaystyle{ \Omega }[/math] is the Rabi frequency. One can approximately calculate the canonical partition function

[math]\displaystyle{ Z = \sum_{ \pm , n} \mathrm{e}^{- \beta E_{\pm}(n)} \approx \sum_{ \pm} \int \mathrm{e}^{- \beta E_{\pm}(n)} dn=\int \mathrm{e}^{\Phi (n)} dn }[/math],

where the discrete sum was replaced by the integral.

The normal approach is that the latter integral is calculated by the Gaussian approximation around the maximum of the exponent:

[math]\displaystyle{ \frac{\partial \Phi(n)} {\partial n}=0 }[/math]

[math]\displaystyle{ \Phi(n)=-\beta \hbar\omega \left(n+\frac{1}{2}\right)+\log 2 \cosh \frac{\hbar \Omega(n) \beta} {2} }[/math]

This leads to the critical equation

[math]\displaystyle{ \tanh \frac{\hbar \Omega(n) \beta} {2}= 4 \frac{\omega}{\Omega}\sqrt{n+1} }[/math]

This has the solution only if

[math]\displaystyle{ \Omega\gt 4 \omega }[/math]

which means that the normal, and the superradiant phase, exist only if the field-atom coupling is significantly stronger than the energy difference between the atom levels. When the condition is fulfilled, the equation gives the solution for the order parameter [math]\displaystyle{ n }[/math] depending on the inverse of the temperature [math]\displaystyle{ 1/\beta }[/math], which means non-vanishing ordered field mode. Similar considerations can be done in true thermodynamic limit of the infinite number of atoms.

Instability of the classical electrostatic model

The better insight on the nature of the superradiant phase transition as well on the physical value of the critical parameter which must be exceeded in order for the transition to occur may be obtained by studying the classical stability of the system of the charged classical harmonic oscillators in the 3D space interacting only with the electrostatic repulsive forces for example between electrons in the locally harmonic oscillator potential. Despite of the original model of the superradiance the quantum electromagnetic field is totally neglected here. The oscillators may be assumed to be placed for example on the cubic lattice with the lattice constant [math]\displaystyle{ a }[/math] in the analogy to the crystal system of the condensed matter. The worse scenario of the defect of the absence of the two out-of-the-plane motion-stabilizing electrons from the 6-th nearest neighbors of a chosen electron is assumed while the four nearest electrons are first assumed to be rigid in space and producing the anti-harmonic potential in the direction perpendicular to the plane of the all five electrons. The condition of the instability of motion of the chosen electron is that the net potential being the superposition of the harmonic oscillator potential and the quadratically expanded Coulomb potential from the four electrons is negative i.e.

[math]\displaystyle{ \frac{m \omega^2}{2}- \frac{1}{2} \times 4 \times \frac {e^2}{4 \pi \epsilon_0} \frac {1}{a^3}\lt 0 }[/math]

or

[math]\displaystyle{ \frac{e^2}{\pi \epsilon_0 m \omega^2}\frac {1}{a^3}\gt 1 }[/math]

Making it artificially quantum by multiplying the numerator and the denominator of the fraction by the [math]\displaystyle{ \hbar }[/math] one obtains the condition

[math]\displaystyle{ \frac{2}{\pi} \frac{|D_{12}|^2}{E_{12} \epsilon_0} \left( \frac{N}{V} \right)\gt 1 }[/math]

where

[math]\displaystyle{ |D_{12}|^2 = \frac{e^2 \hbar} {2 m \omega} }[/math]

is the square of the dipole transition strength between the ground state and the first excited state of the quantum harmonic oscillator,

[math]\displaystyle{ E_{12}=\hbar \omega }[/math]

is the energy gap between consecutive levels and it is also noticed that

[math]\displaystyle{ \frac {1}{a^3}=\frac{N}{V} }[/math]

is the spatial density of the oscillators. The condition is almost identical to this obtained in the original discovery of the superradiant phase transition when replacing the harmonic oscillators with two level atoms with the same distance between the energy levels, dipole transition strength, and the density which means that it occurs in the regime when the Coulomb interactions between electrons dominate over locally harmonic oscillatory influence of the atoms. It that sense the free electron gas with [math]\displaystyle{ \omega=0 }[/math] is also purely superradiant.

The critical inequality rewritten yet differently

[math]\displaystyle{ \omega\lt \sqrt{\frac {e^2}{m \pi \epsilon_0} \frac {N}{V}}\approx\sqrt{\frac {e^2}{m \epsilon_0} \frac {N}{V}} }[/math]

expresses the fact that superradiant phase transition occurs when the frequency of the binding atomic oscillators is lower than so called electron gas plasma frequency.

External links

• Old Warsaw School of "No-Go" of the Superradiant Phase Transition, the talk by the 2022 Wigner Medal recipient Iwo Bialynicki-Birula's former PhD student K. Rzążewski