Physics:Polaron
| Condensed matter physics |
|---|
 |
| Phases · Phase transition · QCP |
A polaron is a quasiparticle used in condensed matter physics to understand the interactions between electrons and atoms in a solid material. The polaron concept was proposed by Lev Landau in 1933[1] and Solomon Pekar in 1946[2] to describe an electron moving in a dielectric crystal where the atoms displace from their equilibrium positions to effectively screen the charge of an electron, known as a phonon cloud. This lowers the electron mobility and increases the electron's effective mass.
The general concept of a polaron has been extended to describe other interactions between the electrons and ions in metals that result in a bound state, or a lowering of energy compared to the non-interacting system. Major theoretical work has focused on solving Fröhlich and Holstein Hamiltonians. This is still an active field of research to find exact numerical solutions to the case of one or two electrons in a large crystal lattice, and to study the case of many interacting electrons.
Experimentally, polarons are important to the understanding of a wide variety of materials. The electron mobility in semiconductors can be greatly decreased by the formation of polarons. Organic semiconductors are also sensitive to polaronic effects, which is particularly relevant in the design of organic solar cells that effectively transport charge. Polarons are also important for interpreting the optical conductivity of these types of materials.
The polaron, a fermionic quasiparticle, should not be confused with the polariton, a bosonic quasiparticle analogous to a hybridized state between a photon and an optical phonon.
Polaron theory
The energy spectrum of an electron moving in a periodical potential of rigid crystal lattice is called the Bloch spectrum, which consists of allowed bands and forbidden bands. An electron with energy inside an allowed band moves as a free electron but has an effective mass that differs from the electron mass in vacuum. However, a crystal lattice is deformable and displacements of atoms (ions) from their equilibrium positions are described in terms of phonons. Electrons interact with these displacements, and this interaction is known as electron-phonon coupling. One possible scenario was proposed in the seminal 1933 paper by Lev Landau, which includes the production of a lattice defect such as an F-center and a trapping of the electron by this defect. A different scenario was proposed by Solomon Pekar that envisions dressing the electron with lattice polarization (a cloud of virtual polar phonons). Such an electron with the accompanying deformation moves freely across the crystal, but with increased effective mass.[3] Pekar coined for this charge carrier the term polaron.
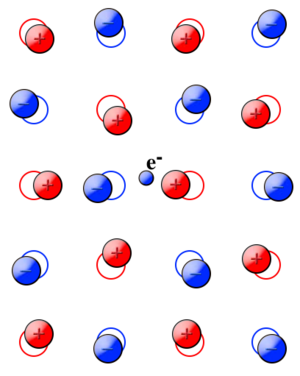
Landau[4] and Pekar[5] constructed the basis of polaron theory. A charge placed in a polarizable medium will be screened. Dielectric theory describes the phenomenon by the induction of a polarization around the charge carrier. The induced polarization will follow the charge carrier when it is moving through the medium. The carrier together with the induced polarization is considered as one entity, which is called a polaron (see Fig. 1).
While polaron theory was originally developed for electrons, there is no fundamental reason why it could not be any other charged particle interacting with phonons. Indeed, other charged particles such as (electron) holes and ions generally follow the polaron theory. For example, the proton polaron was identified experimentally in 2017[6] and on ceramic electrolytes after hypothesis[7] of its existence.
| Material | α | Material | α |
|---|---|---|---|
| InSb | 0.023 | KI | 2.5 |
| InAs | 0.052 | TlBr | 2.55 |
| GaAs | 0.068 | KBr | 3.05 |
| GaP | 0.20 | RbI | 3.16 |
| CdTe | 0.29 | Bi12SiO20 | 3.18 |
| ZnSe | 0.43 | CdF2 | 3.2 |
| CdS | 0.53 | KCl | 3.44 |
| AgBr | 1.53 | CsI | 3.67 |
| AgCl | 1.84 | SrTiO3 | 3.77 |
| α-Al2O3 | 2.40 | RbCl | 3.81 |
Usually, in covalent semiconductors the couplings of electrons with lattice deformation is weak and the formation of polarons does not occur. In polar semiconductors the electrostatic interaction with induced polarization is strong and polarons are formed at low temperature, provided that the concentration of polarons is not large and the screening is not efficient. Another class of materials where polarons are observed is molecular crystals, where the interaction with molecular vibrations may be strong. In the case of polar semiconductors the interaction with polar phonons is described by the Fröhlich Hamiltonian. On the other hand, the interaction of electrons with molecular phonons is described by the Holstein Hamiltonian. Usually the models describing polarons may be divided to two classes. The first class represents continuum models where the discreteness of the crystal lattice is neglected. In that case polarons are weakly coupled or strongly coupled depending on whether the polaron binding energy is small or large compared to the phonon frequency. The second class of systems commonly considered are lattice models of polarons. In this case there may be small or large polarons, depending on the relation of the polaron radius and the lattice constant a.
A conduction electron in an ionic crystal or a polar semiconductor is the prototype of a polaron. Herbert Fröhlich proposed a model Hamiltonian for this polaron through which its dynamics are treated quantum mechanically (Fröhlich Hamiltonian).[10][11] The strength of electron phonon interaction is determined by the dimensionless coupling constant [math]\displaystyle{ \alpha = (e^2 / \kappa)(m / 2 \hbar^3\omega)^{1/2} }[/math]. Here [math]\displaystyle{ m }[/math] is electron mass, [math]\displaystyle{ \omega }[/math] is the phonon frequency and [math]\displaystyle{ \kappa^{-1} = {\epsilon}_{\infin}^{-1} - {\epsilon}_{0}^{-1} }[/math], [math]\displaystyle{ {\epsilon}_{0} }[/math], [math]\displaystyle{ {\epsilon}_{\infin} }[/math] are static and high frequency dielectric constants. In table 1 the Fröhlich coupling constant is given for a few solids. The Fröhlich Hamiltonian for a single electron in a crystal using second quantization notation is:
- [math]\displaystyle{ H = H_{\rm e} + H_{\rm ph} + H_{\rm e-ph} }[/math]
- [math]\displaystyle{ H_{\rm e} = \sum_{k,s} \xi(k,s) c_{k,s}^\dagger c_{k,s} }[/math]
- [math]\displaystyle{ H_{\rm ph} = \sum_{q,v} \omega_{q,v} a_{q,v}^\dagger a_{q,v} }[/math]
- [math]\displaystyle{ H_{\rm e-ph} = \frac 1 {\sqrt{2N} } \sum_{k,s,q,v} \gamma(\alpha , q , k , v ) \omega_{qv} ( c_{k ,s}^\dagger c_{k-q , s} a_{q,v} + c_{k-q ,s}^\dagger c_{k , s} a^\dagger_{q,v} ) }[/math]
The exact form of γ depends on the material and the type of phonon being used in the model. In the case of a single polar mode [math]\displaystyle{ \gamma(q) = i\hbar\omega(\frac{4\pi\alpha}{V_0}(\frac{\hbar}{m\omega})^{1/2})^{1/2}\frac{1}{q} }[/math], here [math]\displaystyle{ V_0 }[/math] is the volume of the unit cell. In the case of molecular crystal γ is usually momentum independent constant. A detailed advanced discussion of the variations of the Fröhlich Hamiltonian can be found in J. T. Devreese and A. S. Alexandrov.[12] The terms Fröhlich polaron and large polaron are sometimes used synonymously, since the Fröhlich Hamiltonian includes the continuum approximation and long range forces. There is no known exact solution for the Fröhlich Hamiltonian with longitudinal optical (LO) phonons and linear [math]\displaystyle{ \gamma }[/math] (the most commonly considered variant of the Fröhlich polaron) despite extensive investigations.[5][9][10][11][13][14][15][16][17][18]
Despite the lack of an exact solution, some approximations of the polaron properties are known.
The physical properties of a polaron differ from those of a band-carrier. A polaron is characterized by its self-energy [math]\displaystyle{ \Delta E }[/math], an effective mass [math]\displaystyle{ m^* }[/math] and by its characteristic response to external electric and magnetic fields (e. g. dc mobility and optical absorption coefficient).
When the coupling is weak ([math]\displaystyle{ \alpha }[/math] small), the self-energy of the polaron can be approximated as:[19]
- [math]\displaystyle{ \frac{\Delta E}{\hbar\omega } \approx -\alpha -0.015919622\alpha^2, \qquad \qquad \qquad (1)\, }[/math]
and the polaron mass [math]\displaystyle{ m* }[/math], which can be measured by cyclotron resonance experiments, is larger than the band mass [math]\displaystyle{ m }[/math] of the charge carrier without self-induced polarization:[20]
- [math]\displaystyle{ \frac{m^*}{m} \approx 1+\frac{\alpha}{6}+0.0236\alpha^2. \qquad \qquad \qquad (2) }[/math]
When the coupling is strong (α large), a variational approach due to Landau and Pekar indicates that the self-energy is proportional to α² and the polaron mass scales as α⁴. The Landau–Pekar variational calculation[5] yields an upper bound to the polaron self-energy [math]\displaystyle{ E \lt -C_{PL} \alpha^2 }[/math], valid for all α, where [math]\displaystyle{ C_{PL} }[/math] is a constant determined by solving an integro-differential equation. It was an open question for many years whether this expression was asymptotically exact as α tends to infinity. Finally, Donsker and Varadhan,[21] applying large deviation theory to Feynman's path integral formulation for the self-energy, showed the large α exactitude of this Landau–Pekar formula. Later, Lieb and Thomas[22] gave a shorter proof using more conventional methods, and with explicit bounds on the lower order corrections to the Landau–Pekar formula.
Feynman[23] introduced the variational principle for path integrals to study the polaron. He simulated the interaction between the electron and the polarization modes by a harmonic interaction between a hypothetical particle and the electron. The analysis of an exactly solvable ("symmetrical") 1D-polaron model,[24][25] Monte Carlo schemes[26][27] and other numerical schemes[28] demonstrate the remarkable accuracy of Feynman's path-integral approach to the polaron ground-state energy. Experimentally more directly accessible properties of the polaron, such as its mobility and optical absorption, have been investigated subsequently.
In the strong coupling limit, [math]\displaystyle{ \alpha \gg 1 }[/math], the spectrum of excited states of a polaron begins with polaron-phonon bound states with energies less than [math]\displaystyle{ \hbar\omega_0 }[/math], where [math]\displaystyle{ \omega_0 }[/math] is the frequency of optical phonons.[29]
In the lattice models the main parameter is the polaron binding energy: [math]\displaystyle{ E_p = \frac{1}{2N}\sum_{q}|\gamma(q)|^{2}/\hbar\omega }[/math],[30] here summation is taken over the Brillouin zone. Note that this binding energy is purely adiabatic, i.e. does not depend on the ionic masses. For polar crystals the value of the polaron binding energy is strictly determined by the dielectric constants [math]\displaystyle{ \epsilon_0 }[/math],[math]\displaystyle{ \epsilon_\infin }[/math], and is of the order of 0.3-0.8 eV. If polaron binding energy [math]\displaystyle{ E_p }[/math] is smaller than the hopping integral t the large polaron is formed for some type of electron-phonon interactions. In the case when [math]\displaystyle{ E_p \gt t }[/math] the small polaron is formed. There are two limiting cases in the lattice polaron theory. In the physically important adiabatic limit [math]\displaystyle{ t\gg\hbar\omega }[/math] all terms which involve ionic masses are cancelled and formation of polaron is described by nonlinear Schrödinger equation with nonadiabatic correction describing phonon frequency renormalization and polaron tunneling.[18][31] [32] In the opposite limit [math]\displaystyle{ t\ll\hbar\omega }[/math] the theory represents the expansion in [math]\displaystyle{ t/\hbar\omega }[/math].[18]
Polaron optical absorption
The expression for the magnetooptical absorption of a polaron is:[33]
- [math]\displaystyle{ \Gamma(\Omega) \propto -\frac{\operatorname{Im} \Sigma(\Omega)}{\left[\Omega-\omega_{\mathrm{c}}-\operatorname{Re} \Sigma(\Omega)\right]^2 + \left[\operatorname{Im}\Sigma(\Omega)\right]^2}. \qquad\qquad\qquad (3) }[/math]
Here, [math]\displaystyle{ \omega_c }[/math] is the cyclotron frequency for a rigid-band electron. The magnetooptical absorption Γ(Ω) at the frequency Ω takes the form Σ(Ω) is the so-called "memory function", which describes the dynamics of the polaron. Σ(Ω) depends also on α, β[clarification needed] and [math]\displaystyle{ \omega_{c} }[/math].
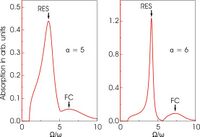
In the absence of an external magnetic field ([math]\displaystyle{ \omega_{c}=0 }[/math]) the optical absorption spectrum (3) of the polaron at weak coupling is determined by the absorption of radiation energy, which is reemitted in the form of LO phonons. At larger coupling, [math]\displaystyle{ \alpha \ge 5.9 }[/math], the polaron can undergo transitions toward a relatively stable internal excited state called the "relaxed excited state" (RES) (see Fig. 2). The RES peak in the spectrum also has a phonon sideband, which is related to a Franck–Condon-type transition.
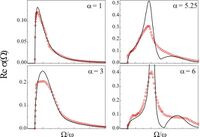
A comparison of the DSG results [34] with the optical conductivity spectra given by approximation-free numerical [35] and approximate analytical approaches is given in ref.[36]
Calculations of the optical conductivity for the Fröhlich polaron performed within the Diagrammatic Quantum Monte Carlo method,[35] see Fig. 3, fully confirm the results of the path-integral variational approach[34] at [math]\displaystyle{ \alpha \lesssim 3. }[/math] In the intermediate coupling regime [math]\displaystyle{ 3\lt \alpha \lt 6, }[/math] the low-energy behavior and the position of the maximum of the optical conductivity spectrum of ref.[35] follow well the prediction of Devreese.[34] There are the following qualitative differences between the two approaches in the intermediate and strong coupling regime: in ref.,[35] the dominant peak broadens and the second peak does not develop, giving instead rise to a flat shoulder in the optical conductivity spectrum at [math]\displaystyle{ \alpha =6 }[/math]. This behavior can be attributed to the optical processes with participation of two[37] or more phonons. The nature of the excited states of a polaron needs further study.
The application of a sufficiently strong external magnetic field allows one to satisfy the resonance condition [math]\displaystyle{ \Omega =\omega_{\mathrm{c}} + \operatorname{Re} \Sigma (\Omega ) }[/math], which {(for [math]\displaystyle{ \omega_c \lt \omega }[/math])} determines the polaron cyclotron resonance frequency. From this condition also the polaron cyclotron mass can be derived. Using the most accurate theoretical polaron models to evaluate [math]\displaystyle{ \Sigma (\Omega ) }[/math], the experimental cyclotron data can be well accounted for.
Evidence for the polaron character of charge carriers in AgBr and AgCl was obtained through high-precision cyclotron resonance experiments in external magnetic fields up to 16 T.[38] The all-coupling magneto-absorption calculated in ref.,[33] leads to the best quantitative agreement between theory and experiment for AgBr and AgCl. This quantitative interpretation of the cyclotron resonance experiment in AgBr and AgCl[38] by the theory of Peeters[33] provided one of the most convincing and clearest demonstrations of Fröhlich polaron features in solids.
Experimental data on the magnetopolaron effect, obtained using far-infrared photoconductivity techniques, have been applied to study the energy spectrum of shallow donors in polar semiconductor layers of CdTe.[39]
The polaron effect well above the LO phonon energy was studied through cyclotron resonance measurements, e. g., in II–VI semiconductors, observed in ultra-high magnetic fields.[40] The resonant polaron effect manifests itself when the cyclotron frequency approaches the LO phonon energy in sufficiently high magnetic fields.
In the lattice models the optical conductivity is given by the formula:[30]
- [math]\displaystyle{ \sigma(\Omega) = n_pe^2a^2 \frac{\pi^{\frac{1}{2}}t^2\left(1-e^{\frac{\hbar\Omega}{k_{\rm B}T}}\right)}{2\hbar^2\Omega(E_ak_{\rm B}T)^{1/2}}\exp\left(-\frac{(\hbar\Omega-4E_a)^2}{16E_ak_{\rm B}T}\right) }[/math]
Here [math]\displaystyle{ E_a }[/math] is the activation energy of polaron, which is of the order of polaron binding energy [math]\displaystyle{ E_p }[/math]. This formula was derived and extensively discussed in[41][42][43] and was tested experimentally for example in photodoped parent compounds of high temperature superconductors.[44]
Polarons in two dimensions and in quasi-2D structures
The great interest in the study of the two-dimensional electron gas (2DEG) has also resulted in many investigations on the properties of polarons in two dimensions.[45][46][47] A simple model for the 2D polaron system consists of an electron confined to a plane, interacting via the Fröhlich interaction with the LO phonons of a 3D surrounding medium. The self-energy and the mass of such a 2D polaron are no longer described by the expressions valid in 3D; for weak coupling they can be approximated as:[48][49]
- [math]\displaystyle{ \frac{\Delta E}{\hbar \omega} \approx -\frac{\pi}{2}\alpha\ - 0.06397\alpha^2; \qquad \qquad \qquad (4)\, }[/math]
- [math]\displaystyle{ \frac{m^*}{m} \approx 1+\frac{\pi}{8}\alpha\ + 0.1272348\alpha^2. \qquad \qquad \qquad (5)\, }[/math]
It has been shown that simple scaling relations exist, connecting the physical properties of polarons in 2D with those in 3D. An example of such a scaling relation is:[47]
- [math]\displaystyle{ \frac{m^{*}_{\rm 2D}(\alpha)}{m_{\rm 2D}}=\frac{m^{*}_{\rm 3D}(\frac{3}{4}\pi\alpha)}{m_{\rm 3D}}, \qquad \qquad \qquad (6)\, }[/math]
where [math]\displaystyle{ m_\mathrm{2D}^* }[/math] ([math]\displaystyle{ m_\mathrm{3D}^* }[/math]) and [math]\displaystyle{ m_\mathrm{2D} }[/math] ([math]\displaystyle{ m_\mathrm{3D} }[/math]) are, respectively, the polaron and the electron-band masses in 2D (3D).
The effect of the confinement of a Fröhlich polaron is to enhance the effective polaron coupling. However, many-particle effects tend to counterbalance this effect because of screening.[45][50]
Also in 2D systems cyclotron resonance is a convenient tool to study polaron effects. Although several other effects have to be taken into account (nonparabolicity of the electron bands, many-body effects, the nature of the confining potential, etc.), the polaron effect is clearly revealed in the cyclotron mass. An interesting 2D system consists of electrons on films of liquid He.[51][52] In this system the electrons couple to the ripplons of the liquid He, forming "ripplopolarons". The effective coupling can be relatively large and, for some values of the parameters, self-trapping can result. The acoustic nature of the ripplon dispersion at long wavelengths is a key aspect of the trapping.
For GaAs/AlxGa1−xAs quantum wells and superlattices, the polaron effect is found to decrease the energy of the shallow donor states at low magnetic fields and leads to a resonant splitting of the energies at high magnetic fields. The energy spectra of such polaronic systems as shallow donors ("bound polarons"), e. g., the D0 and D− centres, constitute the most complete and detailed polaron spectroscopy realised in the literature.[53]
In GaAs/AlAs quantum wells with sufficiently high electron density, anticrossing of the cyclotron-resonance spectra has been observed near the GaAs transverse optical (TO) phonon frequency rather than near the GaAs LO-phonon frequency.[54] This anticrossing near the TO-phonon frequency was explained in the framework of the polaron theory.[55]
Besides optical properties,[9][17][56] many other physical properties of polarons have been studied, including the possibility of self-trapping, polaron transport,[57][58] magnetophonon resonance, etc.
Extensions of the polaron concept
Significant are also the extensions of the polaron concept: acoustic polaron, piezoelectric polaron, electronic polaron, bound polaron, trapped polaron, spin polaron, molecular polaron, solvated polarons, polaronic exciton, Jahn-Teller polaron, small polaron, bipolarons and many-polaron systems.[9] These extensions of the concept are invoked, e. g., to study the properties of conjugated polymers, colossal magnetoresistance perovskites, high-[math]\displaystyle{ T_{c} }[/math] superconductors, layered MgB2 superconductors, fullerenes, quasi-1D conductors, semiconductor nanostructures.
The possibility that polarons and bipolarons play a role in high-[math]\displaystyle{ T_{c} }[/math] superconductors has renewed interest in the physical properties of many-polaron systems and, in particular, in their optical properties. Theoretical treatments have been extended from one-polaron to many-polaron systems.[9][59][60]
A new aspect of the polaron concept has been investigated for semiconductor nanostructures: the exciton-phonon states are not factorizable into an adiabatic product Ansatz, so that a non-adiabatic treatment is needed.[61] The non-adiabaticity of the exciton-phonon systems leads to a strong enhancement of the phonon-assisted transition probabilities (as compared to those treated adiabatically) and to multiphonon optical spectra that are considerably different from the Franck–Condon progression even for small values of the electron-phonon coupling constant as is the case for typical semiconductor nanostructures.[61]
In biophysics Davydov soliton is a propagating along the protein α-helix self-trapped amide I excitation that is a solution of the Davydov Hamiltonian. The mathematical techniques that are used to analyze Davydov's soliton are similar to some that have been developed in polaron theory. In this context the Davydov soliton corresponds to a polaron that is (i) large so the continuum limit approximation in justified, (ii) acoustic because the self-localization arises from interactions with acoustic modes of the lattice, and (iii) weakly coupled because the anharmonic energy is small compared with the phonon bandwidth.[62]
It has been shown that the system of an impurity in a Bose–Einstein condensate is also a member of the polaron family.[63] This allows the hitherto inaccessible strong coupling regime to be studied, since the interaction strengths can be externally tuned through the use of a Feshbach resonance. This was recently realized experimentally by two research groups.[64][65] The existence of the polaron in a Bose–Einstein condensate was demonstrated for both attractive and repulsive interactions, including the strong coupling regime and dynamically observed.[66]
See also
- Exciton
- Sigurd Zienau
- TI-polaron
References
- ↑ L. D. Landau, Electron motion in crystal lattices, Phys. Z. Sowjetunion 3, 664 (1933), in German
- ↑ S. I. Pekar, Journ. of Phys. USSR 10, 341 (1946)
- ↑ L. D. Landau and S. I. Pekar, Effective mass of a polaron, Zh. Eksp. Teor. Fiz. 18, 419–423 (1948) [in Russian], English translation: Ukr. J. Phys., Special Issue, 53, pp. 71–74 (2008), "Archived copy". http://ujp.bitp.kiev.ua/files/journals/53/si/53SI15p.pdf.
- ↑ Landau LD (1933). "Über die Bewegung der Elektronen in Kristallgitter". Phys. Z. Sowjetunion 3: 644–645.
- ↑ 5.0 5.1 5.2 Pekar SI (1951). "Issledovanija po Elektronnoj Teorii Kristallov". Gostekhizdat, Moskva.. English translation: Research in Electron Theory of Crystals, AEC-tr-555, US Atomic Energy Commission (1963)
- ↑ Braun Artur and Chen Qianli (2017). "Experimental neutron scattering evidence for proton polaron in hydrated metal oxide proton conductors". Nature Communications 8: 15830. doi:10.1038/ncomms15830. PMID 28613274. Bibcode: 2017NatCo...815830B.
- ↑ Samin A. L. (2000). "Lattice-assisted proton motion in perovskite oxides". Solid State Ionics 136 (1–2): 291–295. doi:10.1016/S0167-2738(00)00406-9.
- ↑ Devreese JTL (1979). "Moles agitat mentem. Ontwikkelingen in de fysica van de vaste stof". Rede Uitgesproken Bij de Aanvaarding van het Ambt van Buitengewoon Hoogleraar in de Fysica van de Vaste Stof, in Het Bijzonder de Theorie van de Vaste Stof, Bij de Afdeling der Technische Natuurkunde Aan de Technische Hogeschool Eindhoven.
- ↑ 9.0 9.1 9.2 9.3 9.4 "Polarons". Encyclopedia of Physics. 2. 2005. pp. 2004–2027. OCLC 475139057.
- ↑ 10.0 10.1 Fröhlich H; Pelzer H; Zienau S (1950). "Properties of slow electrons in polar materials". Phil. Mag. 41 (314): 221. doi:10.1080/14786445008521794.
- ↑ 11.0 11.1 Fröhlich H (1954). "Electrons in lattice fields". Adv. Phys. 3 (11): 325. doi:10.1080/00018735400101213. Bibcode: 1954AdPhy...3..325F.
- ↑ J. T. Devreese; A. S. Alexandrov (2009). "Fröhlich polaron and bipolaron: recent developments". Rep. Prog. Phys. 72 (6): 066501. doi:10.1088/0034-4885/72/6/066501. Bibcode: 2009RPPh...72f6501D.
- ↑ Kuper GC, ed (1963). "Polarons and Excitons". Oliver and Boyd, Edinburgh.
- ↑ Appel J (1968). "Polarons". In: Solid State Physics, F. Seitz, D. Turnbull, and H. Ehrenreich (Eds.), Academic Press, New York 21: 193–391.
- ↑ 15.0 15.1 Devreese JTL, ed (1972). "Polarons in Ionic Crystals and Polar Semiconductors". North-Holland, Amsterdam.
- ↑ Mitra TK; Chatterjee A; Mukhopadhyay S (1987). "Polarons". Phys. Rep. 153 (2–3): 91. doi:10.1016/0370-1573(87)90087-1. Bibcode: 1987PhR...153...91M.
- ↑ 17.0 17.1 Devreese JTL (1996). "Polarons". In" Encyclopedia of Applied Physics, G. L. Trigg (Ed.), VCH, Weinheim 14: 383–413.
- ↑ 18.0 18.1 18.2 Alexandrov AS; Mott N (1996). "Polarons and Bipolarons". World Scientific, Singapore.
- ↑ Smondyrev MA (1986). "Diagrams in the polaron model". Theor. Math. Phys. 68 (1): 653. doi:10.1007/BF01017794. Bibcode: 1986TMP....68..653S.
- ↑ Röseler J (1968). "A new variational ansatz in the polaron theory". Physica Status Solidi B 25 (1): 311. doi:10.1002/pssb.19680250129. Bibcode: 1968PSSBR..25..311R.
- ↑ Donsker, M. D.; Varadhan, S. R. S. (1983). "Asymptotics for the polaron" (in en). Communications on Pure and Applied Mathematics 36 (4): 505–528. doi:10.1002/cpa.3160360408. ISSN 1097-0312.
- ↑ Lieb E. H.; Thomas L. E. (1997). "Exact Ground State Energy of the Strong Coupling Polaron". Commun. Math. Phys. 183 (3): 511–519. doi:10.1007/s002200050040. Bibcode: 1997CMaPh.183..511L.
- ↑ Feynman RP (1955). "Slow Electrons in a Polar Crystal". Phys. Rev. 97 (3): 660. doi:10.1103/PhysRev.97.660. Bibcode: 1955PhRv...97..660F. https://authors.library.caltech.edu/3544/1/FEYpr55.pdf.
- ↑ Devreese JTL; Evrard R (1964). "On the excited states of a symmetrical polaron model". Phys. Lett. 11 (4): 278. doi:10.1016/0031-9163(64)90324-5. Bibcode: 1964PhL....11..278D.
- ↑ Devreese JTL; Evrard R (1968). "Investigation of the Quadratic approximation in the theory of slow electrons in ionic crystals". Proceedings of the British Ceramic Society 10: 151.
- ↑ Mishchenko AS; Prokof'ev NV; Sakamoto A; Svistunov BV (2000). "Diagrammatic quantum Monte Carlo study of the Fröhlich polaron". Phys. Rev. B 62 (10): 6317. doi:10.1103/PhysRevB.62.6317. Bibcode: 2000PhRvB..62.6317M.
- ↑ Titantah JT; Pierleoni C; Ciuchi S (2001). "Free Energy of the Fröhlich Polaron in Two and Three Dimensions". Phys. Rev. Lett. 87 (20): 206406. doi:10.1103/PhysRevLett.87.206406. PMID 11690499. Bibcode: 2001PhRvL..87t6406T.
- ↑ De Filippis G; Cataudella V; Marigliano Ramaglia V; Perroni CA et al. (2003). "Ground state features of the Fröhlich model". Eur. Phys. J. B 36 (1): 65–73. doi:10.1140/epjb/e2003-00317-x. Bibcode: 2003EPJB...36...65D.
- ↑ V. I. Mel'nikov and E. I. Rashba. ZhETF Pis Red., 10 1969, 95, 359 (1959), JETP Lett 10, 60 (1969). http://www.jetpletters.ac.ru/ps/1687/article_25692.pdf
- ↑ 30.0 30.1 Alexandrov AS; Devreese JTL (2010). Advances in polaron physics. Springer Series in Solid-State physics. 159. Heidelberg: Springer-Verlag. doi:10.1007/978-3-642-01896-1. ISBN 978-3-642-01895-4. Bibcode: 2010app..book.....A. https://cds.cern.ch/record/1315636.
- ↑ Alexandrov AS; Kabanov VV; Ray DK (1994). "From electron to small polaron: An exact cluster solution". Phys. Rev. B 49 (14): 9915–9923. doi:10.1103/PhysRevB.49.9915. PMID 10009793. Bibcode: 1994PhRvB..49.9915A. https://figshare.com/articles/journal_contribution/9408572.
- ↑ Kabanov VV; Mashtakov OYu (1993). "Electron localization with and without barrier formation". Phys. Rev. B 47 (10): 6060–6064. doi:10.1103/PhysRevB.47.6060. PMID 10004555. Bibcode: 1993PhRvB..47.6060K.
- ↑ 33.0 33.1 33.2 Peeters FM; Devreese JTL (1986). "Magneto-optical absorption of polarons". Phys. Rev. B 34 (10): 7246–7259. doi:10.1103/PhysRevB.34.7246. PMID 9939380. Bibcode: 1986PhRvB..34.7246P.
- ↑ 34.0 34.1 34.2 34.3 34.4 Devreese JTL; De Sitter J; Goovaerts M (1972). "Optical Absorption of Polarons in the Feynman–Hellwarth–Iddings–Platzman Approximation". Phys. Rev. B 5 (6): 2367. doi:10.1103/PhysRevB.5.2367. Bibcode: 1972PhRvB...5.2367D.
- ↑ 35.0 35.1 35.2 35.3 35.4 Mishchenko AS; Nagaosa N; Prokof'ev NV; Sakamoto A et al. (2003). "Optical Conductivity of the Fröhlich Polaron". Phys. Rev. Lett. 91 (23): 236401. doi:10.1103/PhysRevLett.91.236401. PMID 14683203. Bibcode: 2003PhRvL..91w6401M.
- ↑ De Filippis G; Cataudella V; Mishchenko AS; Perroni CA et al. (2006). "Validity of the Franck-Condon Principle in the Optical Spectroscopy: Optical Conductivity of the Fröhlich Polaron". Phys. Rev. Lett. 96 (13): 136405. doi:10.1103/PhysRevLett.96.136405. PMID 16712012. Bibcode: 2006PhRvL..96m6405D.
- ↑ Goovaerts M J; De Sitter J; Devreese J T L (1973). "Numerical Study of Two-Phonon Sidebands in the Optical Absorption of Free Polarons in the Strong-Coupling Limit". Phys. Rev. 7 (6): 2639. doi:10.1103/PhysRevB.7.2639. Bibcode: 1973PhRvB...7.2639G.
- ↑ 38.0 38.1 Hodby JW; Russell GP; Peeters F; Devreese JTL et al. (1987). "Cyclotron resonance of polarons in the silver halides: AgBr and AgCl". Phys. Rev. Lett. 58 (14): 1471–1474. doi:10.1103/PhysRevLett.58.1471. PMID 10034445. Bibcode: 1987PhRvL..58.1471H.
- ↑ Grynberg M; Huant S; Martinez G; Kossut J et al. (15 July 1996). "Magnetopolaron effect on shallow indium donors in CdTe". Physical Review B 54 (3): 1467–70. doi:10.1103/physrevb.54.1467. PMID 9985974. Bibcode: 1996PhRvB..54.1467G.
- ↑ Miura N; Imanaka Y (2003). "Polaron cyclotron resonance in II–VI compounds at high magnetic fields". Physica Status Solidi B 237 (1): 237. doi:10.1002/pssb.200301781. Bibcode: 2003PSSBR.237..237M.
- ↑ Eagles DM (1963). "Optical Absorption in Ionic Crystals Involving Small Polarons". Phys. Rev. 130 (4): 1381. doi:10.1103/PhysRev.130.1381. Bibcode: 1963PhRv..130.1381E.
- ↑ Klinger MI (1963). "Quantum theory of non-steady-state conductivity in low mobility solids". Physics Letters 7 (2): 102–104. doi:10.1016/0031-9163(63)90622-X. Bibcode: 1963PhL.....7..102K.
- ↑ Reik HG (1963). "Optical properties of small polarons in the infrared.". Solid State Commun. 1 (3): 67–71. doi:10.1016/0038-1098(63)90360-0. Bibcode: 1963SSCom...1...67R.
- ↑ Mihailović D; Foster CM; Voss K; Heeger AJ (1990). "Application of the polaron-transport theory to σ(ω) in Tl2Ba2Ca1−xGdxCu2O8, YBa2Cu3O7−δ, and La2−xSrxCuO4". Phys. Rev. B 42 (13): 7989–7993. doi:10.1103/PhysRevB.42.7989. PMID 9994964.
- ↑ 45.0 45.1 Devreese JTL, ed (1987). "The Physics of the Two-Dimensional Electron Gas". ASI Series, Plenum, New York B157.
- ↑ Wu XG; Peeters FM; Devreese JTL (1986). "Effect of screening on the optical absorption of a two-dimensional electron gas in GaAs-AlxGa1−xAs heterostructures". Phys. Rev. B 34 (4): 2621–2626. doi:10.1103/PhysRevB.34.2621. PMID 9939955. Bibcode: 1986PhRvB..34.2621W.
- ↑ 47.0 47.1 Peeters FM; Devreese JTL (1987). "Scaling relations between the two- and three-dimensional polarons for static and dynamical properties". Phys. Rev. B 36 (8): 4442–4445. doi:10.1103/PhysRevB.36.4442. PMID 9943430. Bibcode: 1987PhRvB..36.4442P.
- ↑ Sak J (1972). "Theory of Surface Polarons". Phys. Rev. B 6 (10): 3981. doi:10.1103/PhysRevB.6.3981. Bibcode: 1972PhRvB...6.3981S.
- ↑ Peeters FM; Wu XG; Devreese JTL (1988). "Exact and approximate results for the mass of a two-dimensional polaron". Phys. Rev. B 37 (2): 933–936. doi:10.1103/PhysRevB.37.933. PMID 9944589. Bibcode: 1988PhRvB..37..933P.
- ↑ Das Sarma S; Mason BA (1985). "Optical phonon interaction effects in layered semiconductor structures". Annals of Physics 163 (1): 78. doi:10.1016/0003-4916(85)90351-3. Bibcode: 1985AnPhy.163...78S.
- ↑ Shikin VB; Monarkha YP (1973). "Free electrons on the surface of liquid helium in the presence of external fields". Sov. Phys. JETP 38: 373.
- ↑ Jackson SA; Platzman PM (1981). "Polaronic aspects of two-dimensional electrons on films of liquid He". Phys. Rev. B 24 (1): 499. doi:10.1103/PhysRevB.24.499. Bibcode: 1981PhRvB..24..499J.
- ↑ Shi JM; Peeters FM; Devreese JTL (1993). "Magnetopolaron effect on shallow donor states in GaAs". Phys. Rev. B 48 (8): 5202–5216. doi:10.1103/PhysRevB.48.5202. PMID 10009035. Bibcode: 1993PhRvB..48.5202S.
- ↑ Poulter AJL; Zeman J; Maude DK; Potemski M et al. (2001). "Magneto Infrared Absorption in High Electron Density GaAs Quantum Wells". Phys. Rev. Lett. 86 (2): 336–9. doi:10.1103/PhysRevLett.86.336. PMID 11177825. Bibcode: 2001PhRvL..86..336P.
- ↑ Klimin SN; Devreese JTL (2003). "Cyclotron resonance of an interacting polaron gas in a quantum well: Magnetoplasmon-phonon mixing". Phys. Rev. B 68 (24): 245303. doi:10.1103/PhysRevB.68.245303. Bibcode: 2003PhRvB..68x5303K.
- ↑ Calvani P (2001). "Optical Properties of Polarons". Editrice Compositori, Bologna.
- ↑ Feynman RP; Hellwarth RW; Iddings CK; Platzman PM (1962). "Mobility of Slow Electrons in a Polar Crystal". Phys. Rev. 127 (4): 1004. doi:10.1103/PhysRev.127.1004. Bibcode: 1962PhRv..127.1004F. https://resolver.caltech.edu/CaltechAUTHORS:FEYpr62.
- ↑ Yan B; Wan D; Chi X; Li C; Motapothula MR; Hooda S; Yang P; Huang Z et al. (2018). "Anatase TiO2—A model system for large polaron transport". ACS Applied Materials & Interfaces 10 (44): 38201–38208. doi:10.1021/acsami.8b11643. PMID 30362340. https://pubs.acs.org/doi/abs/10.1021/acsami.8b11643.
- ↑ Bassani FG; Cataudella V; Chiofalo ML; De Filippis G et al. (2003). "Electron gas with polaronic effects: beyond the mean-field theory". Physica Status Solidi B 237 (1): 173. doi:10.1002/pssb.200301763. Bibcode: 2003PSSBR.237..173B.
- ↑ Hohenadler M; Hager G; Wellein G; Fehske H (2007). "Carrier-density effects in many-polaron systems". J. Phys.: Condens. Matter 19 (25): 255210. doi:10.1088/0953-8984/19/25/255210. Bibcode: 2007JPCM...19y5210H.
- ↑ 61.0 61.1 Fomin VM; Gladilin VN; Devreese JTL; Pokatilov EP et al. (1998). "Photoluminescence of spherical quantum dots". Phys. Rev. B 57 (4): 2415. doi:10.1103/PhysRevB.57.2415. Bibcode: 1998PhRvB..57.2415F.
- ↑ Scott AS (1992). "Davydov's soliton". Physics Reports 217 (1): 1–67. doi:10.1016/0370-1573(92)90093-F. Bibcode: 1992PhR...217....1S.
- ↑ Tempere J; Casteels W; Oberthaler M; Knoop S et al. (2009). "Feynman path-integral treatment of the BEC-impurity polaron". Phys. Rev. B 80 (18): 184504. doi:10.1103/PhysRevB.80.184504. Bibcode: 2009PhRvB..80r4504T.
- ↑ Jørgensen NB; Wacker L; Skalmstang KT (2016). "Observation of Attractive and Repulsive Polarons in a Bose-Einstein Condensate". Phys. Rev. Lett. 117 (5): 055302. doi:10.1103/PhysRevLett.117.055302. PMID 27517777. Bibcode: 2016PhRvL.117e5302J.
- ↑ Hu M; Van de Graaff MJ; Kedar D; Corson JP et al. (2016). "Bose Polarons in the Strongly Interacting Regime". Phys. Rev. Lett. 117 (5): 055301. doi:10.1103/PhysRevLett.117.055301. PMID 27517776. Bibcode: 2016PhRvL.117e5301H.
- ↑ Skou M; Skov T; Jorgensen N; Nielsen K et al. (2021). "Non-equilibrium quantum dynamics and formation of the Bose polaron". Nature Physics 17 (6): 731–735. doi:10.1038/s41567-021-01184-5. Bibcode: 2021NatPh..17..731S.
External links
 |