Physics:Thin lens

Short description: Lens with a thickness that is negligible

A lens may be considered a thin lens if its thickness is much less than the radii of curvature of its surfaces (d ≪ |R₁| and d ≪ |R₂|).

In optics, a thin lens is a lens with a thickness (distance along the optical axis between the two surfaces of the lens) that is negligible compared to the radii of curvature of the lens surfaces. Lenses whose thickness is not negligible are sometimes called thick lenses.

The thin lens approximation ignores optical effects due to the thickness of lenses and simplifies ray tracing calculations. It is often combined with the paraxial approximation in techniques such as ray transfer matrix analysis.

Focal length

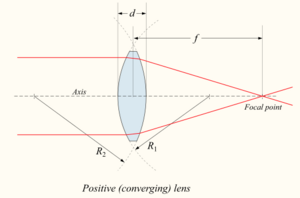
The focal length, f, of a lens in air is given by the lensmaker's equation:

[math]\displaystyle{ \frac{1}{f} = (n-1) \left[ \frac{1}{R_1} - \frac{1}{R_2} + \frac{(n-1)d}{n R_1 R_2} \right], }[/math]

where n is the index of refraction of the lens material, and R₁ and R₂ are the radii of curvature of the two surfaces. For a thin lens, d is much smaller than one of the radii of curvature (either R₁ or R₂). In these conditions, the last term of the Lensmaker's equation becomes negligible, and the focal length of a thin lens in air can be approximated by

[math]\displaystyle{ \frac{1}{f} \approx \left(n-1\right)\left[ \frac{1}{R_1} - \frac{1}{R_2} \right]. }[/math]

Here R₁ is taken to be positive if the first surface is convex, and negative if the surface is concave. The signs are reversed for the back surface of the lens: R₂ is positive if the surface is concave, and negative if it is convex. This is an arbitrary sign convention; some authors choose different signs for the radii, which changes the equation for the focal length.

Derivation using Snell's law

Refraction of a thin planoconvex lens

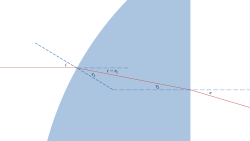
Consider a thin lens with a first surface of radius [math]\displaystyle{ R }[/math] and a flat rear surface, made of material with index of refraction [math]\displaystyle{ n }[/math].

Applying Snell's law, light entering the first surface is refracted according to [math]\displaystyle{ \sin i = n \sin r_1 }[/math], where [math]\displaystyle{ i }[/math] is the angle of incidence on the interface and [math]\displaystyle{ r_1 }[/math] is the angle of refraction.

For the second surface, [math]\displaystyle{ n \sin r_2 = \sin e }[/math], where [math]\displaystyle{ r_2 }[/math] is the angle of incidence and [math]\displaystyle{ e }[/math] is the angle of refraction.

For small angles, [math]\displaystyle{ \sin x \approx x }[/math]. The geometry of the problem then gives:

[math]\displaystyle{ \begin{align} e &\approx n r_2 \\ &= n (i - r_1)\\ &\approx n (i - \frac in) \end{align} }[/math]

Focusing by a thin planoconvex lens

If the incoming ray is parallel to the optical axis and distance [math]\displaystyle{ h }[/math] from it, then [math]\displaystyle{ \sin i = \frac hR \implies i \approx \frac hR. }[/math]

Substituting into the expression above, one gets [math]\displaystyle{ e \approx \frac {h}{R} (n-1). }[/math]

This ray crosses the optical axis at distance [math]\displaystyle{ f }[/math], given by [math]\displaystyle{ \tan e = \frac hf \implies e \approx \frac hf }[/math]

Combining the two expressions gives [math]\displaystyle{ \frac 1f = \frac 1R (n - 1) }[/math].

It can be shown that if two such lenses of radii [math]\displaystyle{ R_1 }[/math] and [math]\displaystyle{ -R_2 }[/math] are placed close together, the focal lengths can be added up giving the thin lens formula:

[math]\displaystyle{ \frac 1f = \left(n-1\right)\left( \frac 1{R_1} - \frac 1{R_2} \right) }[/math]

Image formation

Certain rays follow simple rules when passing through a thin lens, in the paraxial ray approximation:

• Any ray that enters parallel to the axis on one side of the lens proceeds towards the focal point [math]\displaystyle{ f_2 }[/math] on the other side.
• Any ray that arrives at the lens after passing through the focal point [math]\displaystyle{ f_1 }[/math] on the front side, comes out parallel to the axis on the other side.
• Any ray that passes through the center of the lens will not change its direction.

If three such rays are traced from the same point on an object in front of the lens (such as the top), their intersection will mark the location of the corresponding point on the image of the object. By following the paths of these rays, the relationship between the object distance s and the image distance s′ can be shown to be

[math]\displaystyle{ {1\over s} + {1\over s'} = {1\over f} }[/math]

which is known as the thin lens equation.

Physical optics

In scalar wave optics a lens is a part which shifts the phase of the wave-front. Mathematically this can be understood as a multiplication of the wave-front with the following function:

[math]\displaystyle{ \exp\left(\frac{2\pi i}{\lambda} \frac{r^2}{2f}\right) }[/math].