Physics:Tractography
| Tractography | |
|---|---|
| Medical diagnostics | |
 Tractography of human brain | |
| Purpose | used to visually represent nerve tracts |
In neuroscience, tractography is a 3D modeling technique used to visually represent nerve tracts using data collected by diffusion MRI.[1] It uses special techniques of magnetic resonance imaging (MRI) and computer-based diffusion MRI. The results are presented in two- and three-dimensional images called tractograms.[2]
In addition to the long tracts that connect the brain to the rest of the body, there are complicated neural circuits formed by short connections among different cortical and subcortical regions. The existence of these tracts and circuits has been revealed by histochemistry and biological techniques on post-mortem specimens. Nerve tracts are not identifiable by direct exam, CT, or MRI scans. This difficulty explains the paucity of their description in neuroanatomy atlases and the poor understanding of their functions.
The most advanced tractography algorithm can produce 90% of the ground truth bundles, but it still contains a substantial amount of invalid results.[3]
MRI technique
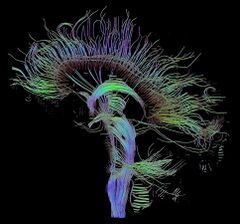
File:Ultra-High-Field-MRI-Post-Mortem-Structural-Connectivity-of-the-Human-Subthalamic-Nucleus-Video1.ogv Tractography is performed using data from diffusion MRI. The free water diffusion is termed "isotropic" diffusion. If the water diffuses in a medium with barriers, the diffusion will be uneven, which is termed anisotropic diffusion. In such a case, the relative mobility of the molecules from the origin has a shape different from a sphere. This shape is often modeled as an ellipsoid, and the technique is then called diffusion tensor imaging. Barriers can be many things: cell membranes, axons, myelin, etc.; but in white matter the principal barrier is the myelin sheath of axons. Bundles of axons provide a barrier to perpendicular diffusion and a path for parallel diffusion along the orientation of the fibers.
Anisotropic diffusion is expected to be increased in areas of high mature axonal order. Conditions where the myelin or the structure of the axon are disrupted, such as trauma,[4] tumors, and inflammation reduce anisotropy, as the barriers are affected by destruction or disorganization.
Anisotropy is measured in several ways. One way is by a ratio called fractional anisotropy (FA). An FA of 0 corresponds to a perfect sphere, whereas 1 is an ideal linear diffusion. Few regions have FA larger than 0.90. The number gives information about how aspherical the diffusion is but says nothing of the direction.
Each anisotropy is linked to an orientation of the predominant axis (predominant direction of the diffusion). Post-processing programs are able to extract this directional information.
This additional information is difficult to represent on 2D grey-scaled images. To overcome this problem, a color code is introduced. Basic colors can tell the observer how the fibers are oriented in a 3D coordinate system, this is termed an "anisotropic map". The software could encode the colors in this way:
- Red indicates directions in the X axis: right to left or left to right.
- Green indicates directions in the Y axis: posterior to anterior or from anterior to posterior.
- Blue indicates directions in the Z axis: foot-to-head direction or vice versa.
The technique is unable to discriminate the "positive" or "negative" direction in the same axis.
Mathematics
Using diffusion tensor MRI, one can measure the apparent diffusion coefficient at each voxel in the image, and after multilinear regression across multiple images, the whole diffusion tensor can be reconstructed.[1]
Suppose there is a fiber tract of interest in the sample. Following the Frenet–Serret formulas, we can formulate the space-path of the fiber tract as a parameterized curve:
- [math]\displaystyle{ \frac{d\mathbf{r}(s)}{ds} = \mathbf{T}(s), }[/math]
where [math]\displaystyle{ \mathbf{T}(s) }[/math] is the tangent vector of the curve. The reconstructed diffusion tensor [math]\displaystyle{ D }[/math] can be treated as a matrix, and we can compute its eigenvalues [math]\displaystyle{ \lambda_1, \lambda_2, \lambda_3 }[/math] and eigenvectors [math]\displaystyle{ \mathbf{u}_1, \mathbf{u}_2, \mathbf{u}_3 }[/math]. By equating the eigenvector corresponding to the largest eigenvalue with the direction of the curve:
- [math]\displaystyle{ \frac{d\mathbf{r}(s)}{ds} = \mathbf{u}_1(\mathbf{r}(s)) }[/math]
we can solve for [math]\displaystyle{ \mathbf{r}(s) }[/math] given the data for [math]\displaystyle{ \mathbf{u}_1(s) }[/math]. This can be done using numerical integration, e.g., using Runge–Kutta, and by interpolating the principal eigenvectors.
See also
References
- ↑ 1.0 1.1 "In vivo fiber tractography using DT-MRI data". Magnetic Resonance in Medicine 44 (4): 625–32. October 2000. doi:10.1002/1522-2594(200010)44:4<625::AID-MRM17>3.0.CO;2-O. PMID 11025519.
- ↑ Catani, Marco; Thiebaut De Schotten, Michel (2012). Atlas of Human Brain Connections. doi:10.1093/med/9780199541164.001.0001. ISBN 978-0-19-954116-4.[page needed]
- ↑ "The challenge of mapping the human connectome based on diffusion tractography". Nature Communications 8 (1): 1349. November 2017. doi:10.1038/s41467-017-01285-x. PMID 29116093. Bibcode: 2017NatCo...8.1349M.
- ↑ Wade, Ryckie G.; Tanner, Steven F.; Teh, Irvin; Ridgway, John P.; Shelley, David; Chaka, Brian; Rankine, James J.; Andersson, Gustav et al. (16 April 2020). "Diffusion Tensor Imaging for Diagnosing Root Avulsions in Traumatic Adult Brachial Plexus Injuries: A Proof-of-Concept Study". Frontiers in Surgery 7: 19. doi:10.3389/fsurg.2020.00019. PMID 32373625.
 |  |
