Physics:Translation operator (quantum mechanics)

In quantum mechanics, a translation operator is defined as an operator which shifts particles and fields by a certain amount in a certain direction. It is a special case of the shift operator from functional analysis. More specifically, for any displacement vector [math]\displaystyle{ \mathbf x }[/math], there is a corresponding translation operator [math]\displaystyle{ \hat{T}(\mathbf{x}) }[/math] that shifts particles and fields by the amount [math]\displaystyle{ \mathbf x }[/math].

For example, if [math]\displaystyle{ \hat{T}(\mathbf{x}) }[/math] acts on a particle located at position [math]\displaystyle{ \mathbf r }[/math], the result is a particle at position [math]\displaystyle{ \mathbf{r}+\mathbf{x} }[/math].

Translation operators are unitary.

Translation operators are closely related to the momentum operator; for example, a translation operator that moves by an infinitesimal amount in the [math]\displaystyle{ y }[/math] direction has a simple relationship to the [math]\displaystyle{ y }[/math]-component of the momentum operator. Because of this relationship, conservation of momentum holds when the translation operators commute with the Hamiltonian, i.e. when laws of physics are translation-invariant. This is an example of Noether's theorem.

Action on position eigenkets and wavefunctions

The translation operator [math]\displaystyle{ \hat{T}(\mathbf{x}) }[/math] moves particles and fields by the amount [math]\displaystyle{ \mathbf x }[/math]. Therefore, if a particle is in an eigenstate [math]\displaystyle{ |\mathbf{r}\rangle }[/math] of the position operator (i.e., precisely located at the position [math]\displaystyle{ \mathbf{r} }[/math]), then after [math]\displaystyle{ \hat{T}(\mathbf{x})= \int\! d\mathbf{r} ~|\mathbf{r+x}\rangle \langle \mathbf{r} | }[/math] acts on it, the particle is at the position [math]\displaystyle{ \mathbf{r} + \mathbf{x} }[/math]: [math]\displaystyle{ \hat{T}(\mathbf{x})|\mathbf{r}\rangle = |\mathbf{r}+\mathbf{x}\rangle . }[/math]

An alternative (and equivalent) way to describe what the translation operator determines is based on position-space wavefunctions. If a particle has a position-space wavefunction [math]\displaystyle{ \psi(\mathbf{r}) }[/math], and [math]\displaystyle{ \hat T(\mathbf{x}) }[/math] acts on the particle, the new position-space wavefunction is [math]\displaystyle{ \psi' (\mathbf{r})= \hat T(\mathbf x) \psi(\mathbf{r}) }[/math] defined by [math]\displaystyle{ \psi'(\mathbf{r}) = \psi(\mathbf{r} - \mathbf{x}). }[/math]

This relation is easier to remember as [math]\displaystyle{ \psi'(\mathbf{r}+\mathbf{x}) = \psi(\mathbf{r}), }[/math] which can be read as: "The value of the new wavefunction at the new point equals the value of the old wavefunction at the old point".

Here is an example showing that these two descriptions are equivalent. The state [math]\displaystyle{ |\mathbf{a}\rangle }[/math] corresponds to the wavefunction [math]\displaystyle{ \psi(\mathbf{r}) = \delta(\mathbf{r} - \mathbf{a}) }[/math] (where [math]\displaystyle{ \delta }[/math] is the Dirac delta function), while the state [math]\displaystyle{ \hat{T}(\mathbf{x})|\mathbf{a}\rangle = |\mathbf{a}+\mathbf{x}\rangle }[/math] corresponds to the wavefunction [math]\displaystyle{ \psi'(\mathbf{r}) = \delta(\mathbf{r} - (\mathbf{a} + \mathbf{x})). }[/math] These indeed satisfy [math]\displaystyle{ \psi'(\mathbf{r}) = \psi(\mathbf{r} - \mathbf{x}) . }[/math]

Momentum as generator of translations

In introductory physics, momentum is usually defined as mass times velocity. However, there is a more fundamental way to define momentum, in terms of translation operators. This is more specifically called canonical momentum, and it is usually but not always equal to mass times velocity; one counterexample is a charged particle in a magnetic field. This definition of momentum is especially important because the law of conservation of momentum applies only to canonical momentum, and is not universally valid if momentum is defined instead as mass times velocity (the so-called "kinetic momentum"), for reasons explained below.

The (canonical) momentum operator is defined as the gradient of the translation operators near the origin:

[math]\displaystyle{ \mathbf{\hat{p}} = i \hbar \left(\nabla \hat{T}(\mathbf{x})\right)_{\text{at }\mathbf{x}=\mathbf{0}} }[/math]

where [math]\displaystyle{ \hbar }[/math] is the reduced Planck's constant. For example, what is the result when the [math]\displaystyle{ \hat{p}_x }[/math] operator acts on a quantum state? To find the answer, translate the state by an infinitesimal amount in the [math]\displaystyle{ x }[/math]-direction, and calculate the rate that the state is changing, and multiply it by [math]\displaystyle{ i \hbar }[/math]. For example, if a state does not change at all when it is translated in the [math]\displaystyle{ x }[/math]-direction, then its [math]\displaystyle{ x }[/math]-component of momentum is 0.

More explicitly, [math]\displaystyle{ \mathbf{\hat{p}} }[/math] is a vector operator (i.e. a vector consisting of three operators [math]\displaystyle{ (\hat{p}_x, \hat{p}_y, \hat{p}_z) }[/math]), defined by: [math]\displaystyle{ \hat{p}_x = i\hbar \lim_{a \to 0} \frac{\hat T(a \mathbf{\hat{x}}) - \hat{\mathbb{I}}}{a} }[/math] where [math]\displaystyle{ \hat{\mathbb{I}} }[/math] is the identity operator and [math]\displaystyle{ \mathbf{\hat{x}} }[/math] is the unit vector in the [math]\displaystyle{ x }[/math]-direction. ([math]\displaystyle{ \hat{p}_y, \hat{p}_z }[/math] are defined analogously.)

The equation above is the most general definition of [math]\displaystyle{ \mathbf{\hat{p}} }[/math]. In the special case of a single particle with wavefunction [math]\displaystyle{ \psi(\mathbf{r}) }[/math], [math]\displaystyle{ \mathbf{\hat{p}} }[/math] can be written in a more specific and useful form. In one dimension: [math]\displaystyle{ \begin{align} (\hat{p}\psi)(r) &= i\hbar \lim_{a\to 0} \frac{(\hat T(a)\psi)(r) - \psi(r)}{a} \\ &= i\hbar \lim_{a\to 0} \frac{\psi(r-a) - \psi(r)}{a} \\ &= -i\hbar \frac{\partial }{\partial r} \psi(r) \end{align} }[/math] or in three dimensions, [math]\displaystyle{ \mathbf{\hat{p}} = -i\hbar \nabla }[/math] as an operator acting on position-space wavefunctions. This is the familiar quantum-mechanical expression for [math]\displaystyle{ \mathbf{\hat{p}} }[/math], but we have derived it here from a more basic starting point.

We have now defined [math]\displaystyle{ \mathbf{\hat{p}} }[/math] in terms of translation operators. It is also possible to write a translation operator as a function of [math]\displaystyle{ \mathbf{\hat{p}} }[/math]. The method consists in expressing a given translation as a huge number [math]\displaystyle{ N }[/math] of consecutive tiny translations, and then use the fact that infinitesimal translations can be written in terms of [math]\displaystyle{ \mathbf{\hat{p}} }[/math]: [math]\displaystyle{ \begin{align} \hat T(\mathbf x) &=\lim_{N \to \infty} (\hat T(\mathbf{x}/N))^N \\ & = \lim_{N \to \infty} \left[1-\frac{i\mathbf{x}\cdot\mathbf\hat{p}}{N\hbar}\right]^N \end{align} }[/math] which gives the final expression:

[math]\displaystyle{ \hat T (\mathbf x) = \exp\left(-\frac{i\mathbf x\cdot\mathbf{\hat p}}{\hbar}\right) = 1 - \frac{i\mathbf x\cdot\mathbf{\hat p}}{\hbar} - \frac{(\mathbf x\cdot\mathbf{\hat p})^2}{2\hbar^2} + \frac{i(\mathbf x\cdot\mathbf{\hat p})^3}{6\hbar^3} + \cdots }[/math]

where [math]\displaystyle{ \exp }[/math] is the operator exponential and the right-hand side is the Taylor series expansion. For very small [math]\displaystyle{ \mathbf{x} }[/math], one can use the approximation: [math]\displaystyle{ \hat T(\mathbf x) \approx 1 - i \mathbf x \cdot \mathbf{\hat p} / \hbar }[/math]

Hence, the momentum operator is referred to as the generator of translation.

A nice way to double-check that these relations are correct is to do a Taylor expansion of the translation operator acting on a position-space wavefunction. Expanding the exponential to all orders, the translation operator generates exactly the full Taylor expansion of a test function: [math]\displaystyle{ \begin{align} \psi(\mathbf{r}-\mathbf{x}) & =\hat T(\mathbf x)\psi(\mathbf{r})\\ & =\exp\left(-\frac{i\mathbf x\cdot\mathbf{\hat p}}{\hbar}\right)\psi(\mathbf{r})\\ & =\left(\sum_{n=0}^{\infty} \frac{1}{n!}(-\frac{i}{\hbar}\mathbf{x}\cdot\mathbf{\hat{p}})^n\right)\psi(\mathbf{r})\\ & =\left(\sum_{n=0}^{\infty} \frac{1}{n!}(-\mathbf{x}\cdot\mathbf{\nabla})^n\right)\psi(\mathbf{r})\\ & =\psi(\mathbf{r})-\mathbf{x}\cdot\mathbf{\nabla}\psi(\mathbf{r})+\frac{1}{2!}(\mathbf{x}\cdot\mathbf{\nabla})^2\psi(\mathbf{r})-\dots \end{align} }[/math] So every translation operator generates exactly the expected translation on a test function if the function is analytic in some domain of the complex plane.

Properties

Successive translations

[math]\displaystyle{ \hat T(\mathbf{x}_1) \hat T(\mathbf{x}_2) = \hat T(\mathbf{x}_1 + \mathbf{x}_2) }[/math]

In other words, if particles and fields are moved by the amount [math]\displaystyle{ \mathbf{x}_2 }[/math] and then by the amount [math]\displaystyle{ \mathbf{x}_1 }[/math], overall they have been moved by the amount [math]\displaystyle{ \mathbf{x}_1 + \mathbf{x}_2 }[/math]. For a mathematical proof, one can look at what these operators do to a particle in a position eigenstate: [math]\displaystyle{ \hat T(\mathbf{x}_1) \hat T(\mathbf{x}_2) |\mathbf{r}\rangle = \hat T(\mathbf{x}_1) |\mathbf{x}_2 + \mathbf{r}\rangle = |\mathbf{x}_1 + \mathbf{x}_2 + \mathbf{r}\rangle = \hat T(\mathbf{x}_1 + \mathbf{x}_2)|\mathbf{r}\rangle }[/math] Since the operators [math]\displaystyle{ \hat T(\mathbf{x}_1) \hat T(\mathbf{x}_2) }[/math] and [math]\displaystyle{ \hat T(\mathbf{x}_1 + \mathbf{x}_2) }[/math] have the same effect on every state in an eigenbasis, it follows that the operators are equal.

Inverse

The translation operators are invertible, and their inverses are: [math]\displaystyle{ (\hat T(\mathbf{x}))^{-1} = \hat T(-\mathbf{x}) }[/math]

This follows from the "successive translations" property above, and the fact that [math]\displaystyle{ \hat T(\mathbf{0}) = \hat{\mathbb{I}} }[/math], i.e. a translation by a distance of 0 is the same as the identity operator which leaves all states unchanged.

Translation operators commute with each other

[math]\displaystyle{ \hat T(\mathbf{x})\hat T(\mathbf{y}) = \hat T(\mathbf{y})\hat T(\mathbf{x}) }[/math] because both sides are equal to [math]\displaystyle{ \hat T(\mathbf{x}+\mathbf{y}) }[/math].

Translation operators are unitary

If [math]\displaystyle{ \psi(\mathbf{r}) }[/math] and [math]\displaystyle{ \phi(\mathbf{r}) }[/math] are two position-space wavefunctions, then the inner product of [math]\displaystyle{ \psi }[/math] with [math]\displaystyle{ \phi }[/math] is: [math]\displaystyle{ \int d^3\mathbf{r}\, \psi^*(\mathbf{r}) \phi(\mathbf{r}) }[/math] while the inner product of [math]\displaystyle{ \hat T(\mathbf{a})\psi }[/math] with [math]\displaystyle{ \hat T(\mathbf{a})\phi }[/math] is: [math]\displaystyle{ \int d^3\mathbf{r}\, \psi^*(\mathbf{r}-\mathbf{a}) \phi(\mathbf{r}-\mathbf{a}) }[/math] By change of variables, these two inner products are exactly the same. Therefore, the translation operators are unitary, and in particular: [math]\displaystyle{ (\hat T(\mathbf{x}))^\dagger = (\hat T(\mathbf{x}))^{-1}. }[/math]

The fact that translation operators are unitary implies that the momentum operator is Hermitian.

Translation Operator operating on a bra

A translation operator [math]\displaystyle{ \hat{T}(\mathbf{x})= \int d\mathbf{r} ~ |\mathbf{r+x}\rangle \langle \mathbf{r} | }[/math] operating on a bra in the position eigenbasis gives: [math]\displaystyle{ \langle \mathbf r| \hat T(\mathbf x) = \langle \mathbf r - \mathbf x| }[/math]

Proof

[math]\displaystyle{ \hat T(\mathbf x)|\mathbf r\rangle = |\mathbf r + \mathbf x\rangle }[/math] Its adjoint expression is: [math]\displaystyle{ \langle \mathbf r|(\hat T(\mathbf{x}))^\dagger = \langle \mathbf r + \mathbf x| }[/math] Using the results above, [math]\displaystyle{ (\hat T(\mathbf{x}))^\dagger = (\hat T(\mathbf{x}))^{-1} = \hat{T}(-\mathbf x) }[/math]: [math]\displaystyle{ \langle \mathbf r| \hat T(-\mathbf x) = \langle \mathbf r + \mathbf x| }[/math] Replacing [math]\displaystyle{ \mathbf x }[/math] by [math]\displaystyle{ -\mathbf x }[/math], [math]\displaystyle{ \langle \mathbf r| \hat T(\mathbf x) = \langle \mathbf r - \mathbf x| }[/math]

Splitting a translation into its components

According to the "successive translations" property above, a translation by the vector [math]\displaystyle{ \mathbf{x} = (x,y,z) }[/math] can be written as the product of translations in the component directions: [math]\displaystyle{ \hat{T}(\mathbf{x}) = \hat{T}(x\mathbf{\hat{x}})\,\hat{T}(y\mathbf{\hat{y}})\,\hat{T}(z\mathbf{\hat{z}}) }[/math] where [math]\displaystyle{ \mathbf{\hat{x}},\mathbf{\hat{y}},\mathbf{\hat{z}} }[/math] are unit vectors.

Commutator with position operator

Suppose [math]\displaystyle{ |\mathbf r\rangle }[/math] is an eigenvector of the position operator [math]\displaystyle{ \mathbf{\hat r} }[/math] with eigenvalue [math]\displaystyle{ \mathbf r }[/math]. We have [math]\displaystyle{ \hat T(\mathbf{x})\mathbf{\hat{r}}|\mathbf r\rangle = \hat T(\mathbf{x})\mathbf{r}|\mathbf r\rangle = \mathbf{r}|\mathbf{x} + \mathbf r\rangle }[/math] while [math]\displaystyle{ \mathbf{\hat{r}}\hat T(\mathbf{x})|\mathbf r\rangle = \hat\mathbf{r}|\mathbf{x} + \mathbf r\rangle = (\mathbf{x} + \mathbf{r}) |\mathbf{x} + \mathbf r\rangle }[/math]

Therefore, the commutator between a translation operator and the position operator is: [math]\displaystyle{ [\mathbf{\hat r},\hat T(\mathbf x)] \equiv \mathbf{\hat r}\hat T(\mathbf x) - \hat T(\mathbf x)\mathbf{\hat r} = \mathbf x \hat T(\mathbf x) }[/math] This can also be written (using the above properties) as: [math]\displaystyle{ (\hat T(\mathbf x))^{-1}\mathbf{\hat r}\hat T(\mathbf x) = \mathbf{\hat r} + \mathbf x\hat{\mathbb{I}} }[/math] where [math]\displaystyle{ \hat{\mathbb{I}} }[/math] is the identity operator.

Commutator with momentum operator

Since translation operators all commute with each other (see above), and since each component of the momentum operator is a sum of two scaled translation operators (e.g. [math]\displaystyle{ \hat{p}_y = \lim_{\varepsilon \to 0} \frac{i\hbar}{\varepsilon} \left( \hat{T}((0, \varepsilon, 0)) - \hat{T}((0,0,0))\right) }[/math]), it follows that translation operators all commute with the momentum operator, i.e. [math]\displaystyle{ \hat T(\mathbf{x}) \hat{\mathbf{p}} = \hat{\mathbf{p}}\hat T(\mathbf{x}) }[/math] This commutation with the momentum operator holds true generally even if the system is not isolated where energy or momentum may not be conserved.

The translation group

The set [math]\displaystyle{ \mathfrak{T} }[/math] of translation operators [math]\displaystyle{ \hat T(\mathbf x) }[/math] for all [math]\displaystyle{ \mathbf x }[/math], with the operation of multiplication defined as the result of successive translations (i.e. function composition), satisfies all the axioms of a group:

Closure

When two translations are done consecutively, the result is a single different translation. (See "successive translations" property above.)

Existence of identity

A translation by the vector [math]\displaystyle{ \mathbf{0} }[/math] is the identity operator, i.e. the operator that has no effect on anything. It functions as the identity element of the group.

Every element has an inverse

As proven above, any translation operator [math]\displaystyle{ \hat T(\mathbf{x}) }[/math] is the inverse of the reverse translation [math]\displaystyle{ \hat T(-\mathbf x) }[/math].

Associativity

This is the claim that [math]\displaystyle{ \hat T(\mathbf{x}_1)\left (\hat T(\mathbf{x}_2) \hat T(\mathbf{x}_3)\right ) = \left (\hat T(\mathbf{x}_1)\hat T(\mathbf{x}_2)\right )\hat T(\mathbf{x}_3) }[/math]. It is true by definition, as is the case for any group based on function composition.

Therefore, the set [math]\displaystyle{ \mathfrak{T} }[/math] of translation operators [math]\displaystyle{ \hat T(\mathbf x) }[/math] for all [math]\displaystyle{ \mathbf x }[/math] forms a group. Since there are continuously infinite number of elements, the translation group is a continuous group. Moreover, the translation operators commute among themselves, i.e. the product of two translation (a translation followed by another) does not depend on their order. Therefore, the translation group is an abelian group.

The translation group acting on the Hilbert space of position eigenstates is isomorphic to the group of vector additions in the Euclidean space.

Expectation values of position and momentum in the translated state

Consider a single particle in one dimension. Unlike classical mechanics, in quantum mechanics a particle neither has a well-defined position nor a well-defined momentum. In the quantum formulation, the expectation values play the role of the classical variables. For example, if a particle is in a state [math]\displaystyle{ |\psi\rangle }[/math], then the expectation value of the position is [math]\displaystyle{ \langle \psi | \mathbf{\hat r} | \psi \rangle }[/math], where [math]\displaystyle{ \mathbf{\hat r} }[/math] is the position operator.

If a translation operator [math]\displaystyle{ \hat T(\mathbf{x}) }[/math] acts on the state [math]\displaystyle{ |\psi\rangle }[/math], creating a new state [math]\displaystyle{ |\psi_2\rangle }[/math] then the expectation value of position for [math]\displaystyle{ |\psi_2\rangle }[/math] is equal to the expectation value of position for [math]\displaystyle{ |\psi\rangle }[/math] plus the vector [math]\displaystyle{ \mathbf{x} }[/math]. This result is consistent with what you would expect from an operation that shifts the particle by that amount.

Proof that a translation operator changes the expectation value of position in the way you would expect

Assume [math]\displaystyle{ |\psi_2\rangle = \hat T(\mathbf{x})|\psi\rangle }[/math] as stated above. [math]\displaystyle{ \begin{align} \langle \psi_2 | \hat{\mathbf{r}} | \psi_2 \rangle &= (\langle \psi | (\hat{T}(\mathbf{x}))^\dagger) \hat{\mathbf{r}} (\hat{T}(\mathbf{x})| \psi \rangle) \\ &= \langle \psi | \hat{\mathbf{r}} | \psi \rangle + \mathbf{x} \end{align} }[/math] using the normalization condition [math]\displaystyle{ \langle\psi|\psi\rangle = 1 }[/math], and the commutator result proven in a previous section.

On the other hand, when the translation operator acts on a state, the expectation value of the momentum is not changed. This can be proven in a similar way as the above, but using the fact that translation operators commute with the momentum operator. This result is again consistent with expectations: translating a particle does not change its velocity or mass, so its momentum should not change.

Translational invariance

In quantum mechanics, the Hamiltonian represents the energy and dynamics of a system. Let [math]\displaystyle{ |\mathbf{r}_T\rangle\equiv \hat{T}|\mathbf{r}\rangle }[/math]be a newly translated state (the argument of [math]\displaystyle{ \hat{T}(\mathbf{x}) }[/math] is irrelevant here and is temporarily dropped for brevity). A Hamiltonian is said to be invariant if [math]\displaystyle{ \langle \mathbf{r}_T|\hat{H}|\mathbf{r}_T\rangle = \langle \mathbf{r}|\hat H|\mathbf{r}\rangle }[/math] or [math]\displaystyle{ \langle \mathbf{r}|\hat{T}^{-1}\hat{H}\hat{T}|\mathbf{r}\rangle = \langle \mathbf{r}|\hat H|\mathbf{r}\rangle }[/math] This implies that [math]\displaystyle{ \hat{T}^{-1}\hat{H}\hat{T}=\hat {H} }[/math] [math]\displaystyle{ \hat{H}\hat{T}-\hat{T}\hat {H}=[\hat{H},\hat{T}]=0 }[/math]

Thus, if the Hamiltonian is invariant under translation, the Hamiltonian commutes with the translation operator (loosely speaking, if we translate the system, then measure its energy, then translate it back, it amounts to the same thing as just measuring its energy directly).

Continuous translational symmetry

First we consider the case where all the translation operators are symmetries of the system. As we will see, in this case conservation of momentum occurs.

For example, if [math]\displaystyle{ \hat{H} }[/math] is the Hamiltonian describing all particles and fields in the universe, and [math]\displaystyle{ \hat T(\mathbf x) }[/math] is the translation operator that shifts all particles and fields in the universe simultaneously by the same amount, then this is always a symmetry: [math]\displaystyle{ \hat{H} }[/math] describes the complete laws of physics in our universe, which are independent of location. As a consequence, conservation of momentum is universally valid.

On the other hand, perhaps [math]\displaystyle{ \hat{H} }[/math] and [math]\displaystyle{ \hat T(\mathbf x) }[/math] refer to just one particle. Then the translation operators [math]\displaystyle{ \hat T(\mathbf x) }[/math] are exact symmetries only if the particle is alone in a vacuum. Correspondingly, the momentum of a single particle is not usually conserved (it changes when the particle bumps into other objects), but it is conserved if the particle is alone in a vacuum.

Since the Hamiltonian commutes with the translation operator when the translation is invariant [math]\displaystyle{ \left[\hat H,\hat T(\mathbf{x})\right]=0\,, }[/math] it also commutes with the infinitesimal translation operator [math]\displaystyle{ \begin{align} &\left[\hat H, 1-\frac{i\mathbf{x}\cdot \hat\mathbf{p}}{N\hbar}\right]=0\\ & \Rightarrow [\hat H,\hat{\mathbf p}]=0 \\ & \Rightarrow \frac{d}{dt}\langle\hat{\mathbf p}\rangle= \frac{i}{\hbar}[\hat H,\hat{\mathbf p}]=0 \end{align} }[/math] In summary, whenever the Hamiltonian for a system remains invariant under continuous translation, then the system has conservation of momentum, meaning that the expectation value of the momentum operator remains constant. This is an example of Noether's theorem.

Discrete translational symmetry

There is another special case where the Hamiltonian may be translationally invariant. This type of translational symmetry is observed whenever the potential is periodic: [math]\displaystyle{ V(r_j\pm a)=V(r_j) }[/math] In general, the Hamiltonian is not invariant under any translation represented by [math]\displaystyle{ \hat T_j(x_j) }[/math] with [math]\displaystyle{ x_j }[/math] arbitrary, where [math]\displaystyle{ \hat T_j(x_j) }[/math] has the property: [math]\displaystyle{ \hat T_j(x_j)|r_j\rangle=|r_j+x_j\rangle }[/math] and, [math]\displaystyle{ (\hat{T}_j(x_j))^\dagger \hat r_j\hat T_j(x_j)=\hat r_j+x_j\hat{\mathbb{I}} }[/math] (where [math]\displaystyle{ \hat{\mathbb{I}} }[/math] is the identity operator; see proof above).

But, whenever [math]\displaystyle{ x_j }[/math] coincides with the period of the potential [math]\displaystyle{ a }[/math], [math]\displaystyle{ (\hat{T}_j(a))^\dagger V(\hat r_j)\hat T_j(a)=V(\hat r_j+a\hat{\mathbb{I}})=V(\hat r_j) }[/math] Since the kinetic energy part of the Hamiltonian [math]\displaystyle{ \hat H }[/math] is already invariant under any arbitrary translation, being a function of [math]\displaystyle{ \mathbf{\hat p} }[/math], the entire Hamiltonian satisfies, [math]\displaystyle{ (\hat{T}_j(a))^\dagger \hat H\hat T_j(a)=\hat H }[/math] Now, the Hamiltonian commutes with translation operator, i.e. they can be simultaneously diagonalised. Therefore, the Hamiltonian is invariant under such translation (which no longer remains continuous). The translation becomes discrete with the period of the potential.

Discrete translation in periodic potential: Bloch's theorem

The ions in a perfect crystal are arranged in a regular periodic array. So we are led to the problem of an electron in a potential [math]\displaystyle{ V(\mathbf{r}) }[/math] with the periodicity of the underlying Bravais lattice [math]\displaystyle{ V(\mathbf{r}+\mathbf{R})=V(\mathbf r ) }[/math] for all Bravais lattice vectors [math]\displaystyle{ \mathbf R }[/math]

However, perfect periodicity is an idealisation. Real solids are never absolutely pure, and in the neighbourhood of the impurity atoms the solid is not the same as elsewhere in the crystal. Moreover, the ions are not in fact stationary, but continually undergo thermal vibrations about their equilibrium positions. These destroy the perfect translational symmetry of a crystal. To deal with this type of problems the main problem is artificially divided in two parts: (a) the ideal fictitious perfect crystal, in which the potential is genuinely periodic, and (b) the effects on the properties of a hypothetical perfect crystal of all deviations from perfect periodicity, treated as small perturbations.

Although, the problem of electrons in a solid is in principle a many-electron problem, in independent electron approximation each electron is subjected to the one-electron Schrödinger equation with a periodic potential and is known as Bloch electron (in contrast to free particles, to which Bloch electrons reduce when the periodic potential is identically zero.)

For each Bravais lattice vector [math]\displaystyle{ \mathbf R }[/math] we define a translation operator [math]\displaystyle{ \hat T_{\mathbf R} }[/math] which, when operating on any function [math]\displaystyle{ f(\mathbf r) }[/math] shifts the argument by [math]\displaystyle{ \mathbf R }[/math]: [math]\displaystyle{ \hat T_{\mathbf R}f(\mathbf r)=f(\mathbf r+\mathbf R) }[/math] Since all translations form an Abelian group, the result of applying two successive translations does not depend on the order in which they are applied, i.e. [math]\displaystyle{ \hat T_{\mathbf R_1}\hat T_{\mathbf R_2}=\hat T_{\mathbf R_2}\hat T_{\mathbf R_1}=\hat T_{\mathbf {R}_1 + \mathbf{R}_2} }[/math] In addition, as the Hamiltonian is periodic, we have, [math]\displaystyle{ \hat T_{\mathbf R}\hat H=\hat H\hat T_{\mathbf R} }[/math] Hence, the [math]\displaystyle{ \hat T_{\mathbf R} }[/math] for all Bravais lattice vectors [math]\displaystyle{ \mathbf R }[/math] and the Hamiltonian [math]\displaystyle{ \hat H }[/math] form a set of commutating operators. Therefore, the eigenstates of [math]\displaystyle{ \hat H }[/math] can be chosen to be simultaneous eigenstates of all the [math]\displaystyle{ \hat T_{\mathbf R} }[/math]: [math]\displaystyle{ \hat H\psi=\mathcal E\psi }[/math] [math]\displaystyle{ \hat T_{\mathbf R}\psi=c(\mathbf R)\psi }[/math]

The eigenvalues [math]\displaystyle{ c(\mathbf R) }[/math] of the translation operators are related because of the condition: [math]\displaystyle{ \hat T_{\mathbf R_1}\hat T_{\mathbf R_2}=\hat T_{\mathbf R_2}\hat T_{\mathbf R_1}=\hat T_{\mathbf R_1 + \mathbf R_2} }[/math] We have, [math]\displaystyle{ \begin{align} \hat T_{\mathbf R_1}\hat T_{\mathbf R_2}\psi & =c(\mathbf R_1)\hat T_{\mathbf R_2}\psi\\ & =c(\mathbf R_1)c(\mathbf R_2)\psi \end{align} }[/math] And, [math]\displaystyle{ \hat T_{\mathbf {R_1 +R_2}}\psi=c(\mathbf R_1+\mathbf R_2)\psi }[/math] Therefore, it follows that, [math]\displaystyle{ c(\mathbf R_1+\mathbf R_2)=c(\mathbf R_1)c(\mathbf R_2) }[/math] Now let the [math]\displaystyle{ \mathbf{a}_i }[/math]'s be the three primitive vector for the Bravais lattice. By a suitable choice of [math]\displaystyle{ x_i }[/math], we can always write [math]\displaystyle{ c(\mathbf{a}_i) }[/math] in the form [math]\displaystyle{ c(\mathbf{a}_i)=e^{2\pi ix_i} }[/math] If [math]\displaystyle{ \mathbf R }[/math] is a general Bravais lattice vector, given by [math]\displaystyle{ \mathbf R=n_1\mathbf a_1+n_2\mathbf a_2+n_3\mathbf a_3 }[/math] it follows then, [math]\displaystyle{ \begin{align} c(\mathbf R) & =c(n_1\mathbf a_1+n_2\mathbf a_2+n_3\mathbf a_3)\\ & =c(n_1\mathbf a_1)c(n_2\mathbf a_2)c(n_3\mathbf a_3)\\ & =c(\mathbf a_1)^{n_1}c(\mathbf a_2)^{n_2}c(\mathbf a_3)^{n_3} \end{align} }[/math] Substituting [math]\displaystyle{ c(\mathbf{a}_i)=e^{2\pi ix_i} }[/math] one gets, [math]\displaystyle{ \begin{align} c(\mathbf R) & =e^{2\pi i(n_1x_1+n_2x_2+n_3x_3)}\\ & = e^{i\mathbf k\cdot\mathbf R} \end{align} }[/math] where [math]\displaystyle{ \mathbf{k} = x_1 \mathbf{b}_1 + x_2 \mathbf{b}_2 + x_3 \mathbf{b}_3 }[/math] and the [math]\displaystyle{ \mathbf b_i }[/math]'s are the reciprocal lattice vectors satisfying the equation [math]\displaystyle{ \mathbf b_i\cdot\mathbf a_j=2\pi\delta_{ij} }[/math]

Therefore, one can choose the simultaneous eigenstates [math]\displaystyle{ \psi }[/math] of the Hamiltonian [math]\displaystyle{ \hat H }[/math] and [math]\displaystyle{ \hat T_{\mathbf R} }[/math] so that for every Bravais lattice vector [math]\displaystyle{ \mathbf R }[/math], [math]\displaystyle{ \begin{align} \psi(\mathbf{r+R}) & =\hat T_{\mathbf R}\psi(\mathbf r)\\ & = c(\mathbf R)\psi(\mathbf r)\\ & =e^{i\mathbf k\cdot\mathbf R}\psi(\mathbf r) \end{align} }[/math] So,

[math]\displaystyle{ \psi(\mathbf{r+R})=e^{i\mathbf k\cdot\mathbf R}\psi(\mathbf r) }[/math]

This result is known as Bloch's Theorem.

Time evolution and translational invariance

Translational Invariance: Time evolution of the wave functions.

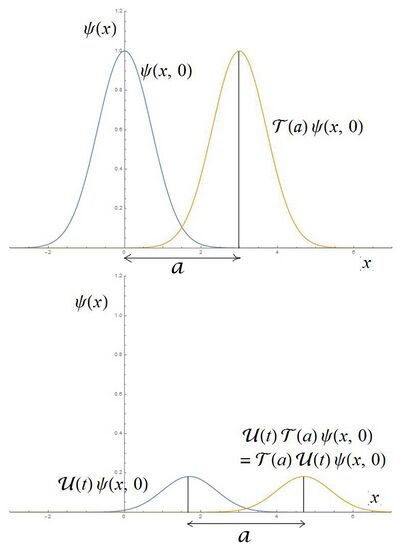
In the passive transformation picture, translational invariance requires, [math]\displaystyle{ [\hat T(\mathbf{x}),\hat H] = 0 }[/math] It follows that [math]\displaystyle{ [\hat T(\mathbf{x}),\hat U(t)] = 0 }[/math] where [math]\displaystyle{ \hat U(t) }[/math] is the unitary time evolution operator. When the Hamiltonian is time independent, [math]\displaystyle{ \hat U(t)= \exp\left(\frac{-i\hat H t}{\hbar}\right) }[/math] If the Hamiltonian is time dependent, the above commutation relation is satisfied if [math]\displaystyle{ \hat p }[/math] or [math]\displaystyle{ \hat T(\mathbf x) }[/math] commutes with [math]\displaystyle{ \hat H (t) }[/math] for all t.

Example

Suppose at [math]\displaystyle{ t=0 }[/math] two observers A and B prepare identical systems at [math]\displaystyle{ x=0 }[/math] and [math]\displaystyle{ x=a }[/math] (fig. 1), respectively. If [math]\displaystyle{ |\psi(0)\rangle }[/math] be the state vector of the system prepared by A, then the state vector of the system prepared by B will be given by [math]\displaystyle{ \hat T(\mathbf{a})|\psi(0)\rangle }[/math] Both the systems look identical to the observers who prepared them. After time [math]\displaystyle{ t }[/math], the state vectors evolve into [math]\displaystyle{ \hat U (t)|\psi(0)\rangle }[/math] and [math]\displaystyle{ \hat U (t) \hat T(\mathbf{a})|\psi(0)\rangle }[/math] respectively. Using the above-mentioned commutation relation, the later may be written as, [math]\displaystyle{ \hat T(\mathbf{a})\hat U(t)|\psi(0)\rangle }[/math] which is just the translated version of the system prepared by A at time [math]\displaystyle{ t }[/math]. Therefore, the two systems, which differed only by a translation at [math]\displaystyle{ t=0 }[/math], differ only by the same translation at any instant of time. The time evolution of both the systems appear the same to the observers who prepared them. It can be concluded that the translational invariance of Hamiltonian implies that the same experiment repeated at two different places will give the same result (as seen by the local observers).

See also

• Bloch state
• Group
• Periodic function
• Shift operator
• Symmetries in quantum mechanics
• Time translation symmetry
• Translational symmetry