Physics:Type-I superconductor

Short description: Type of superconductor with a single critical magnetic field

Phase diagram (B, T) of a type I superconductor : if B < B_c, the medium is superconducting. T_c is the critical temperature of a superconductor when there is no magnetic field.

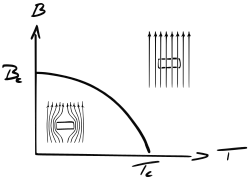
The interior of a bulk superconductor cannot be penetrated by a weak magnetic field, a phenomenon known as the Meissner effect. When the applied magnetic field becomes too large, superconductivity breaks down. Superconductors can be divided into two types according to how this breakdown occurs. In type-I superconductors, superconductivity is abruptly destroyed via a first order phase transition when the strength of the applied field rises above a critical value H_c. This type of superconductivity is normally exhibited by pure metals, e.g. aluminium, lead, and mercury. The only alloy known up to now which exhibits type I superconductivity is tantalum silicide (TaSi₂). The covalent superconductor SiC:B, silicon carbide heavily doped with boron, is also type-I.

Depending on the demagnetization factor, one may obtain an intermediate state. This state, first described by Lev Landau, is a phase separation into macroscopic non-superconducting and superconducting domains forming a Husimi Q representation.

This behavior is different from type-II superconductors which exhibit two critical magnetic fields. The first, lower critical field occurs when magnetic flux vortices penetrate the material but the material remains superconducting outside of these microscopic vortices. When the vortex density becomes too large, the entire material becomes non-superconducting; this corresponds to the second, higher critical field.

The ratio of the London penetration depth λ to the superconducting coherence length ξ determines whether a superconductor is type-I or type-II. Type-I superconductors are those with [math]\displaystyle{ 0 \lt \tfrac{\lambda}{\xi} \lt \tfrac{1}{\sqrt{2}} }[/math], and type-II superconductors are those with [math]\displaystyle{ \tfrac{\lambda}{\xi} \gt \tfrac{1}{\sqrt{2}} }[/math].