Physics:Husimi Q representation
The Husimi Q representation, introduced by Kôdi Husimi in 1940,[1] is a quasiprobability distribution commonly used in quantum mechanics[2] to represent the phase space distribution of a quantum state such as light in the phase space formulation.[3] It is used in the field of quantum optics[4] and particularly for tomographic purposes. It is also applied in the study of quantum effects in superconductors.[5]
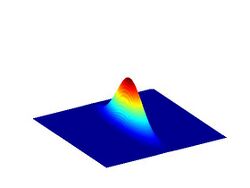
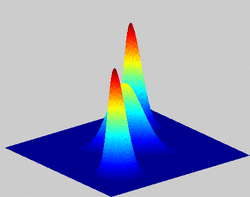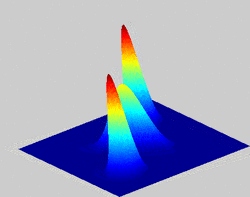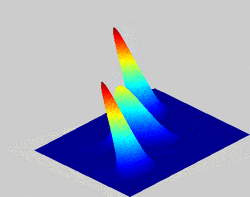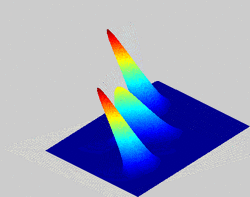
Definition and properties
The Husimi Q distribution (called Q-function in the context of quantum optics) is one of the simplest distributions of quasiprobability in phase space. It is constructed in such a way that observables written in anti-normal order follow the optical equivalence theorem. This means that it is essentially the density matrix put into normal order. This makes it relatively easy to calculate compared to other quasiprobability distributions through the formula
- [math]\displaystyle{ Q(\alpha)=\frac{1}{\pi}\langle\alpha|\hat{\rho}|\alpha\rangle, }[/math]
which is proportional to a trace of the operator [math]\displaystyle{ \hat{\rho}|\alpha\rangle \langle\alpha| }[/math] involving the projection to the coherent state [math]\displaystyle{ |\alpha\rangle }[/math]. It produces a pictorial representation of the state ρ to illustrate several of its mathematical properties.[6] Its relative ease of calculation is related to its smoothness compared to other quasiprobability distributions. In fact, it can be understood as the Weierstrass transform of the Wigner quasiprobability distribution, i.e. a smoothing by a Gaussian filter,
- [math]\displaystyle{ Q(\alpha)= \frac{2}{\pi} \int W(\beta) e^{-2|\alpha-\beta|^2} \, d^2\beta. }[/math]
Such Gauss transforms being essentially invertible in the Fourier domain via the convolution theorem, Q provides an equivalent description of quantum mechanics in phase space to that furnished by the Wigner distribution.
Alternatively, one can compute the Husimi Q distribution by taking the Segal–Bargmann transform of the wave function and then computing the associated probability density.
Q is normalized to unity,
- [math]\displaystyle{ \int Q(\alpha)\,d\alpha^2 = 1 }[/math]
and is non-negative definite[7] and bounded:
- [math]\displaystyle{ 0 \leq Q(\alpha) \leq \frac{1}{\pi}. }[/math]
Despite the fact that Q is non-negative definite and bounded like a standard joint probability distribution, this similarity may be misleading, because different coherent states are not orthogonal. Two different points α do not represent disjoint physical contingencies; thus, Q(α) does not represent the probability of mutually exclusive states, as needed in the third axiom of probability theory.
Q may also be obtained by a different Weierstrass transform of the Glauber–Sudarshan P representation,
- [math]\displaystyle{ Q(\alpha,\alpha^*)= \frac{1}{\pi} \int P(\beta,\beta^*) e^{-|\alpha-\beta|^2} \, d^2\beta, }[/math]
given [math]\displaystyle{ \hat{\rho} = \int P(\beta,\beta^*) |{\beta}\rangle \langle {\beta}|\, d^{2}\beta }[/math], and the standard inner product of coherent states.
See also
- Quasiprobability distribution § Characteristic functions
- Nonclassical light
- Glauber–Sudarshan P-representation
- Wehrl entropy
References
- ↑ Kôdi Husimi (1940). "Some Formal Properties of the Density Matrix", Proc. Phys. Math. Soc. Jpn. 22: 264-314 .
- ↑ Dirac, P. A. M. (1982). The principles of quantum mechanics (Fourth ed.). Oxford UK: Oxford University Press. p. 18 ff. ISBN 0-19-852011-5. https://books.google.com/books?id=XehUpGiM6FIC&q=intitle:quantum+intitle:mechanics+inauthor:dirac.
- ↑ Ulf Leonhardt (1997). Measuring the Quantum State of Light, Cambridge Studies in Modern Optics. ISBN:0521497302 , ISBN:978-0521497305.
- ↑ H. J. Carmichael (2002). Statistical Methods in Quantum Optics I: Master Equations and Fokker-Planck Equations, Springer-Verlag. ISBN:978-3-540-54882-9
- ↑ Callaway, D. J. E. (1990). "On the remarkable structure of the superconducting intermediate state". Nuclear Physics B 344 (3): 627–645. doi:10.1016/0550-3213(90)90672-Z. Bibcode: 1990NuPhB.344..627C.
- ↑ Cosmas K. Zachos, David B. Fairlie, and Thomas L. Curtright (2005). Quantum Mechanics in Phase Space, (World Scientific, Singapore) ISBN:978-981-238-384-6 [1] .
- ↑ Cartwright, N. D. (1975). "A non-negative Wigner-type distribution". Physica A: Statistical Mechanics and Its Applications 83 (1): 210–818. doi:10.1016/0378-4371(76)90145-X. Bibcode: 1976PhyA...83..210C.
 |  |
